1. Легкое женское покрывало из кисеи, шелка, кружев и тому подобное, закрывающее голову и верхнюю часть тела, как часть свадебного наряда невесты.
1. Фаты, (с санскр (итальянское) ). Легкое женское покрывало из кисеи, шелка, кружев и т. падеж Шелковой фатой я закрылася. Лермонтов. Невеста в фате.
ФАТА
(исланд. fat). 1) род покрывала для головы и части стана, которое носили древнерусские женщины. 2) кружевное или тюлевое покрывало невесты.
ФАТА
древне русский(русское) головное женское покрывало; теперь - головн. убор неве степень
ФАТА
покрывало на лицо и на голову, преимущественно из к. кто-нибудь прозрачной материи.
-ы, женский род
Легкое женское покрывало на голову из кисеи, шелка, кружев и т. падеж (у старое ).
Лишь одна не глядит, не любуется, Полосатой фатой закрывается. Лермонтов, Песня про купца Калашникова.
Легкое покрывало из тюля или кружева, служащее свадебным головным убором невесты.
{Невеста} опускается перед отцом на колени, и ее фата волнуется при этом и цепляется за цветы, разбросанные по платью. Чехов, Свадьба.
Наталью, уже одетую в подвенечное платье и фату, стерегли за столом. Шолохов, Тихий Дон.
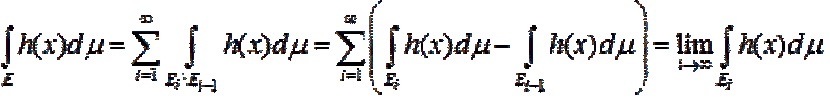... неравенство I Отсюда по теореме 9 имеем неравенство I, что и доказывает . теорему Лемма 4 (Фату ). Пусть на измеримом множестве Е задана последовательность (x),.(x), (x), ¼ измеримых неотрицательных функций , имеющая нижний ... ... 3 и теореме 12 . влечет интегрируемость F(х). Так как g(x) ± fi (x) ³ 0 на множестве . Е, то применяя лемму Фату и теорему 12 , имеем , Мы здесь воспользовались тем, что g(x) ± fi (x) ® g.(x) ± F(х) и тем, что верхний и нижний предел ... (Функциональный анализ)
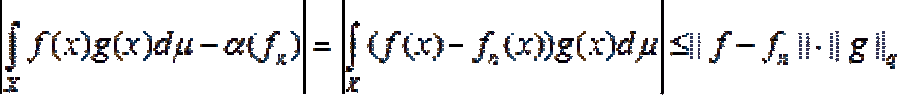... абсолютно п в на X Так как |f(x)|p £ gp (x), то функция f. будет также интегрируемой в степени р Применяя лемму Фату (лемма и неравенство треугольника , мы получим неравенство . Таким образом , = 0, т е существует предел ... (Функциональный анализ)
... . Значит для доказательства теоремы достаточно доказать , что Р(А) =0. и Р(С)= Покажем , что Р(А)= В силу неравенства Чебышева и леммы . Фату имеем Р( Устремляя теперь , получаем Р(А)=. Теперь докажем , что Р(С)= Заметим , что , где и - рациональные числа }==. Рассмотрим ... (вероятностные процессы)
... Р Тогда - супермартингал (относительно меры Р). Доказательство Так как Р - п н для , где - локализующая последовательность , то в силу леммы Фату . Доказательство закончено Займемся теперь классификацией марковских моментов Определение Марковский момент ... (вероятностные процессы)
... обеспечили понимание механизмов регулирования ворот канала посредством лигандов . через и фосфатидилинозитол 4 ,- фат Информация , полученная благодаря анализу кристаллической структуры , чрезвычайно ценна , так как. позволяет оценить ... (Физиология человека, гигиена и возрастная физиология)
... лемма о сходимости последовательностей , 26 лемма Рисса о почти перпендикуляре , 112 лемма Фату , 91 линейно независимые вектора , 106 линейное многообразие , 106 линейное пространство ... (Функциональный анализ)
Комментарии
Оставить комментарий