1. Щеголь, любящий порисоваться, пустой человек.
Пустой щеголь, франт. ФАТА, -ы, ас. Закрывающее голову и верхнюю часть тела легкое женское покрывало из кисеи, кружев, шелка. Свадебная фата.
1. Фата, (фр. fat, буквально жирный). Щеголь, любящий порисоваться, пустой человек. Всегда завит, раздушен, одет по картинке... так, фат! Гончаров. "Какие у нее трагические глаза!" заметил сидевший позади Аратова некий седоватый фат. Тургенев.
ФАТ
(фр. fat, от лат. fatius - глупый, сумасбродный, безвкусный). Самодовольный франт, нахал, пустой человек.
ФАТ
вертопрах; самодовольный франт, пошлый, пустой человек.
ФАТ
пошлый франт, пустой и самодовольный хлыщ.
ФАТ
франц. fat, от лат. fatus, глупый, сумасбродный, безвкусный. Самодовольный лгун.
-а, м.
1.
Самодовольный франт, щеголь, любящий рисоваться, пустой человек.
— Всегда завит, раздушен, одет по картинке: вот и воображает, что все женщины от него без ума — так, фат! И. Гончаров, Обыкновенная история.
2. Театр. у старое
Амплуа актера, игравшего роли эффектных, самовлюбленных, легкомысленных и ограниченных людей (преимущественно молодых).
В прежнее время --- так и составлялась труппа. Был в ней первый герой-любовник и второй герой-любовник; первый салонный любовник, он же и фат. Юрьев, Беседы актера.
{Франц. fat}
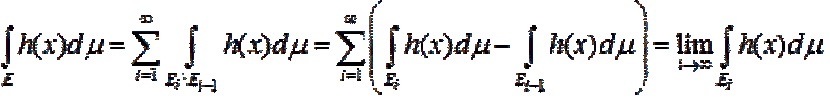... неравенство I Отсюда по теореме 9 имеем неравенство I, что и доказывает . теорему Лемма 4 (Фату ). Пусть на измеримом множестве Е задана последовательность (x),.(x), (x), ¼ измеримых неотрицательных функций , имеющая нижний ... ... 3 и теореме 12 . влечет интегрируемость F(х). Так как g(x) ± fi (x) ³ 0 на множестве . Е, то применяя лемму Фату и теорему 12 , имеем , Мы здесь воспользовались тем, что g(x) ± fi (x) ® g.(x) ± F(х) и тем, что верхний и нижний предел ... (Функциональный анализ)
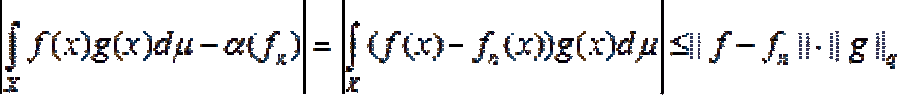... абсолютно п в на X Так как |f(x)|p £ gp (x), то функция f. будет также интегрируемой в степени р Применяя лемму Фату (лемма и неравенство треугольника , мы получим неравенство . Таким образом , = 0, т е существует предел ... (Функциональный анализ)
... . Значит для доказательства теоремы достаточно доказать , что Р(А) =0. и Р(С)= Покажем , что Р(А)= В силу неравенства Чебышева и леммы . Фату имеем Р( Устремляя теперь , получаем Р(А)=. Теперь докажем , что Р(С)= Заметим , что , где и - рациональные числа }==. Рассмотрим ... (вероятностные процессы)
... Р Тогда - супермартингал (относительно меры Р). Доказательство Так как Р - п н для , где - локализующая последовательность , то в силу леммы Фату . Доказательство закончено Займемся теперь классификацией марковских моментов Определение Марковский момент ... (вероятностные процессы)
... обеспечили понимание механизмов регулирования ворот канала посредством лигандов . через и фосфатидилинозитол 4 ,- фат Информация , полученная благодаря анализу кристаллической структуры , чрезвычайно ценна , так как. позволяет оценить ... (Физиология человека, гигиена и возрастная физиология)
... лемма о сходимости последовательностей , 26 лемма Рисса о почти перпендикуляре , 112 лемма Фату , 91 линейно независимые вектора , 106 линейное многообразие , 106 линейное пространство ... (Функциональный анализ)
Комментарии
Оставить комментарий