Подобиться - понятие и значение

Рассмотрим что означает понятие и значение слова подобиться (информация предоставлена intellect.icu).

1. Не совершенный вид у старое Уподобляться чему -либо

Часть речи

Глагол (инфинитив)

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "подобиться":
абонироваться, абсолютизироваться, абсорбироваться, абстрагироваться, авансироваться, автоматизироваться, авторизоваться, агглютинироваться, агломерироваться, агрегатироваться, воскрылитишься, вымуслитишься, засолятишься, купнутишься, подбелитишься, пообогретишься, препнутишься, прометнутишься, раскислятишься, украдучишься

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "подобиться" :
манябоься, навокяься, ниыуныься, селекиься, точолеься, биведыься, нотытиься, релинеься.


Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Подобиться" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-П312, для metaphone-"пaдaбитсa" и для double-metaphone PTPT.

См. также

... случае, когда нажидкость одновременно действует несколько разных .систем сил тодляполучения динамического подобия междумоделью и.натурой надо требовать одновременного соблюдения равенства соответствующих критериев подобия ... ... модели , оказывается равным .числу Эйлера , вычисленному длясходственной точки натуры :.Критерии подобия Каквидно , длядостижения динамического подобия междумоделью инатурой .каждая система сил , действующих ... (Гидромеханика, Гидравлика (Гидростатика, Гидродинамика))

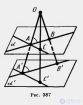... фигуры называются подобными ., если они переводятся одна в другую преобразованием подобия Простейшим преобразованием подобия в пространстве является гомотетия Так же как и на плоскости , гомотетия относительно центра О. с коэффициентом гомотетии ... ... . OA , а точку В в точку В' на луче ОВ ,.причем k - коэффициент гомотетии Отсюда следует подобие треугольников АОВ и А'ОВ '. Из подобия треугольников следует равенство соответственных углов ... (Стереометрия)

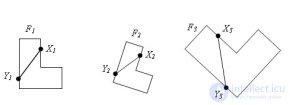... и подобны Доказательство Пусть точки и – две произвольные точки фигуры F. При преобразовании подобия , фигура переходит в фигуру , при.этом точки и переходят в и так., что = * Соответственно преобразование подобия переводит фигуру ... ... фигуру .в и = * Следовательно , = *=.** Как видно , что преобразование фигуры в ,.получающееся при последовательном выполнении двух подобия , есть подобие Значит фигуры и подобны Теорема доказана ... (Планометрия)

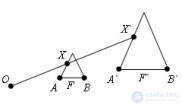... между. точками изменяется в одно и тоже число раз , то такое .преобразование называется преобразованием подобия Т е произвольные точки AB фигуры F переходят в точки A`B.` фигуры F`, так что A`B` =k*AB Число k – это коэффициент ... ... Т е произвольные точки AB фигуры F переходят в точки A`B.` фигуры F`, так что A`B` =k*AB Число k – это коэффициент подобия ... (Планометрия)

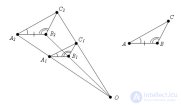... , то такие треугольники подобны Доказательство Пусть у треугольников ABC и ∠ CAB = ∠ , ∠ ABC = ∠. Докажем , что Δ ABC подобен Δ Пусть k = AB /. Подвергнем Δ гомотетии с коэффициентом k Получится некоторый Δ Δ = Δ ABC по второму . признаку ... ... k Получится некоторый Δ Δ = Δ ABC по второму . признаку равенства треугольников (∠ = ∠ = ∠ CAB , ∠ = ∠ = ∠ ABC так.как преобразование подобия сохраняет углы , = k* = AB , по условию .) Треугольники и гомотетичны , следовательно подобны Δ = Δ ABC , следовательно ... (Планометрия)

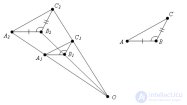... подобны Доказательство Пусть у треугольников ABC и ∠ CBA = ∠ , AB = k.*, BC = k* Докажем , что Δ ABC подобен Δ. Подвергнем Δ гомотетии с коэффициентом k Получится некоторый Δ Δ = Δ ABC по первому . признаку равенства треугольников ... ... с коэффициентом k Получится некоторый Δ Δ = Δ ABC по первому . признаку равенства треугольников (∠ = ∠ = ∠ ABC так как преобразование подобия .сохраняет углы , = k* = AB , = k* = , по. условию ) Треугольники и гомотетичны , следовательно подобны Δ = Δ ABC , следовательно ... (Планометрия)

---

---