8 Моделирование гидравлических процессов. Элементы теории размерностей

Привет, Вы узнаете о том , что такое 8 Моделирование гидравлических процессов. Элементы теории размерностей, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 8 Моделирование гидравлических процессов. Элементы теории размерностей , настоятельно рекомендую прочитать все из категории Гидромеханика, Гидравлика (Гидростатика, Гидродинамика).

При составлении проекта сложных сооружений и объектов часто обращаются к так называемому лабораторному проектированию. При этом в лаборатории создают модель рассматриваемого сооружения (объекта), через которую пропускают воду (или другую жидкость) и измеряют различные величины (давления, скорости и т. п.). Полученные таким образом для модели величины затем переносят на действительное сооружение.

При выполнении такого рода работ возникает целый ряд вопросов: как следует в лаборатории строить модель (какие размеры ей надо придавать, ка-

кую шероховатость стенок должна иметь модель и т. п.); какие величины V и Q надо задавать на модели, если она в определенное число раз меньше действительного сооружения; каким образом данные, полученные в лаборатории для модели, следует переносить на действительное сооружение.

Перечисленными вопросами и занимается теория физического моделирования гидравлических явлений.

Основой указанного моделирования (относящегося к механике жидкости) является так называемая теория подобия, которая опирается на учение о размерности физических величин.

2.3.1. Основные понятия о подобии гидравлических явлений

При физическом моделировании гидравлических явлений различают геометрическое, кинематическое и динамическое подобия.

1. Геометрическое подобие. Две гидравлические системы (два гидравлических явления) будут геометрически подобными в том случае, если между сходственными размерами этих систем всюду существует постоянное соотношение:

(2.41)

где lн — некоторый размер действительного сооружения (натуры); lн — сходственный размер модели; аl, — масштаб длины.

Для геометрически подобных систем

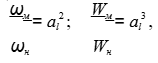(2.42)​

где ωн , Wн — некоторая площадь и некоторый объем, относящиеся к действительному сооружению; ωн , Wн — сходственные площадь и объем модели.

2. Кинематическое подобие. Две гидравлические системы будут кинематически подобными, если:

а) траектории, описываемые сходственными частицами жидкости обеих систем, геометрически подобны и одинаково ориентированы по отношению к границам этих систем;

б) скорости U и ускорения w в сходственных точках в соответственные моменты времени всюду связаны постоянными соотношениями:

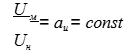(по всему объему); (2.43)

Подчеркнем, что кинематически подобные системы всегда будут геометрически подобными системами.

В связи с кинематическим подобием возникает понятие масштаба времени

(2.45)

где и tн и tм — промежутки времени, в течение которых протекают соответственные явления в натуре и на модели.

Для кинематически подобных систем

at=const (по всему объему).(2.46)

3. Динамическое подобие. Две гидравлические системы будут динамически подобными, если:

а) в любой паре сходственных точек действуют одноименные силы; б) соотношение величин соответствующих сил для любой пары сходст-

венных точек одинаково по всему объему обоих рассматриваемых гидравлических систем, т. е. масштаб сил:

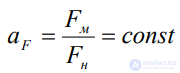(по всему объему), (2.47)

где через F обозначена любая сила, действующая на жидкость;

в) силы, действующие на первую гидравлическую систему, ориентированы относительно друг друга и относительно границ системы так, как и силы, действующие на вторую гидравлическую систему.

Можно сказать, что динамически подобными системами будут такие, для которых векторные поля сил, действующих на жидкость, образованы одноименными силами, причем эти поля являются геометрически подобными и одинаково ориентированными относительно границ систем.

Динамическое подобие может иметь место только при наличии кинематического, а, следовательно, и геометрического подобия. Как видно, динамическое подобие предопределяет существование кинематического подобия. Поэтому динамически подобные системы являются механически подобными системами.

В связи с вопросом о динамическом подобии возникает понятие масштаба плотности жидкости:

(2.48)

Судить о динамическом подобии двух систем (см. выше п. «в») путем измерения и сравнения между собой сил, действующих на эти системы, практически неудобно и даже невозможно. Вместе с тем легко видеть, что соотношение сил, действующих в натуре и на модели, может быть установлено косвенно: по имеющимся масштабам длины, скорости и плотности жидкости, т. е. по соотношению величин, легко поддающихся измерению.

Принимая такой косвенный метод оценки динамического подобия, пользуемся так называемыми критериями динамического подобия.

2.3.2.Критерии динамического подобия

Вобщем случае на движущуюся несжимаемую вязкую жидкость действуют следующие силы:

1) объемная внешняя сила тяжести G;

2) поверхностные (внешние и внутренние) силы гидродинамического давления P;

3) поверхностные (внешние и внутренние) силы трения (вязкости) Т. Геометрическая сумма указанных сил, согласно началу Даламбера, может быть представлена в виде

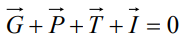(2.49)

где I — сила инерции,

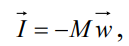(2.50)

причем здесь М — масса выделенного объема жидкости, w — ускорение. При заданных граничных условиях можно считать, что в данной точке

жидкости сила давления Р целиком определяется силами G, Т и I:

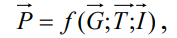(2.51)

поэтому (2.49) можно переписать в виде:

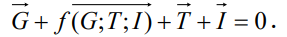(2.52)

Для различных частных случаев уравнение движения (2.52) может упроститься в связи с тем, что некоторые силы, входящие в него, оказываются или равными нулю, или получают пренебрежимо малую величину сравнительно с другими силами. Об этом говорит сайт https://intellect.icu . Например, в случае параллельноструйного установившегося движения сила инерции I = 0. В случае напорного движения в трубопроводе эффект действия собственного веса G рассматриваемого объема жидкости по сравнению с эффектом действия сил давления Р оказывается ничтожным, и потому сила G из уравнения (2.52) может быть исключена. В случае ламинарного движения силы I часто могут оказаться пренебрежимо малыми сравнительно с силами Т, и т.д.

Рассмотрим в начале простейшие случаи, когда на исследуемую жидкость действует только одна система определяющих сил (не считая сил инерции); при этом ограничимся рассмотрением только таких условий движения, при которых силы инерции соизмеримы с силами тяжести или силами внутреннего трения.

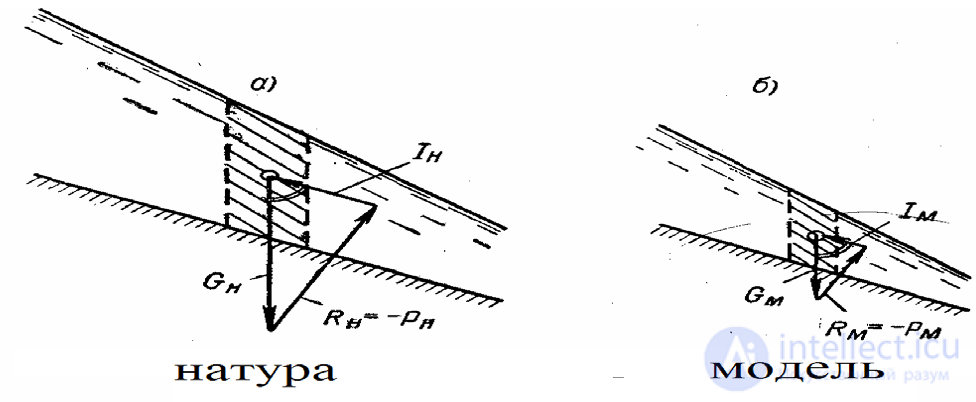
1. Случай, когда на жидкость действуют только силы тяжести. В этом случае в уравнение (2.52) будут входить только сила G и сила инерции I.

Для достижения динамического подобия двух систем (натуры и модели),

изображенных на рис.надо требовать, чтобы треугольники сил, показанных на схемах а и б, были геометрически подобными.

Чтобы обеспечить подобие указанных треугольников сил, необходимо: а) кинематическое подобие двух рассматриваемых систем, так как именно

это условие обеспечит равенство углов, образованных силами G и I на рис. а и б; напомним, что, требуя кинематического подобия, мы тем самым требуем и геометрического подобия;

б) соблюдение равенства

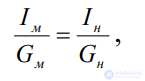(2.53)

или, что то же,

(2.54)

Как видно, масштаб сил в данном случае равен отношению сил инерции,вычисленных для модели и для натуры.

Согласно (2.50),

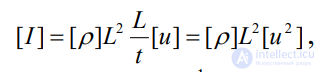(2.55)

где Lи t — символы длины и времени.1

Поэтому масштаб сил аF, обеспечивающий динамическое подобие, в данном случае будет2

(2.56)

Размерность силы тяжести можно представить в виде

(2.57)

следовательно

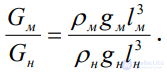(2.58)

Учитывая соотношения (2.56) и (2.58), можем написать, согласно (2.54),

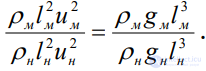(2.59)

Как видно, для достижения динамического подобия, когда на жидкость действует только сила G (а также сила инерции I), необходимо требовать, помимо соблюдения кинематического подобия, еще и соблюдения равенства (2.59), которое можно переписать в виде

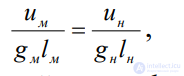(2.60)

где и — скорость в данной точке; l — какой-либо линейный размер; g — ускорение силы тяжести.

1Квадратные скобки в соотношении (2.55) и других указывают, что нас интересует здесь не численное значение, а размерность соответствующих величин.

2Для двух динамически подобных систем справедливость перехода от соотношения (2.55) к соотношению (2.56), где вместо символов, выражающих размерность отдельных величин, проставлены сами величины, может быть строго обоснована (этого обоснования здесь не приводим).

Введем обозначение

(2.61)

Следует подчеркнуть, что величина Fr является безразмерной и представляет собой меру отношения сил инерции к силам тяжести. Эту величину принято называть числом Фруда.

Таким образом, когда на жидкость действуют только силы тяжести, динамическое подобие будет иметь место, если существуют геометрическое и кинематическое подобия и если число Фруда, вычисленное для любой точки модели, оказывается равным числу Фруда, вычисленному для сходственной точки натуры,

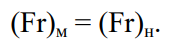(2.62)

2. Случай, когда на жидкость действуют только силы трения (вязкости). Здесь для соблюдения динамического подобия выражение, определяющее масштаб сил, должно остаться прежним [см. равенство (2.56)].

Считая, что силы трения подчиняются зависимости Ньютона (1.6), можем написать

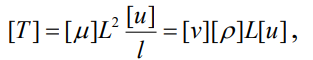(2.63)

откуда получаем

(2.64)

Приравнивая (2.64) соотношению (2.56), получаем

(2.65)

Как видно, для достижения динамического подобия в случае, когда на жидкость действуют сила Т и сила инерции I, необходимо требовать, помимо кинематического подобия, соблюдения равенства (2.65). Это последнее равенство можно переписать в виде

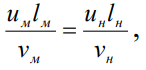(2.66)

где и — скорость в данной точке; l — какой-либо линейный размер, например диаметр трубы D или гидравлический радиус R и т. п.; v— кинематический коэффициент вязкости жидкости.

Следует подчеркнуть, что величина

(обозначение) (2.67)

является безразмерной и представляет собой меру отношения сил инерции к силам трения. С этой величиной мы сталкивались ранее и называли ее числом Рейнольдса.

Таким образом, когда на жидкость действуют только силы трения, динамическое подобие будет иметь место, если существует геометрическое и кинематическое подобие и если число Рейнольдса, вычисленное для любой точки модели, оказывается равным числу Рейнольдса, вычисленному для сходственной точки натуры:

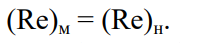(2.68)

3. Случай, когда на жидкость действуют только силы давления. Рассуждая и делая преобразования аналогично п. 1 и п. 2, можно получить величину называемую числом Эйлера.

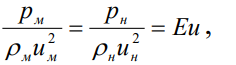(2.69)

Таким образом, когда на жидкость действуют только силы трения, динамическое подобие будет иметь место, если существует геометрическое и кинематическое подобие и если число Эйлера, вычисленное для любой точки модели, оказывается равным числу Эйлера, вычисленному для сходственной точки натуры:

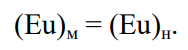(2.70)

Критерии подобия. Как видно, для достижения динамического подобия между моделью и натурой каждая система сил, действующих на жидкость, требует равенства в сходственных точках модели и натуры некоторого своего числа (числу Фруда, числа Рейнольдса и т. д.).

Эти безразмерные числа (Фруда, Рейнольдса, Эйлера, Вебера, Коши и т. д.), равенство которых в сходственных точках модели и натуры указывает на наличие подобая между моделью и натурой, называются критериями подобия.

В общем случае, когда на жидкость одновременно действует несколько разных систем сил то для получения динамического подобия между моделью и натурой надо требовать одновременного соблюдения равенства соответствующих критериев подобия в сходственных живых сечениях.

Если, например, при постановке гидравлических опытов необходимо учитывать как силы тяжести, так и силы трения, то для достижения динамического подобия между моделью и натурой следует, помимо кинематического и геометрического подобий, одновременно выдержать еще два условия:

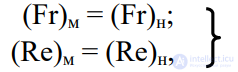
причем эти условия должны относиться ко всем сходственным живым сечениям модели и натуры.

2.3.3.Пи – теорема

Вразличных областях физики имеются величины, являющиеся независимыми. Величины относят к зависимым, если размерность одной из них может быть представлена как комбинация остальных. Примером зависимых величин

являются, например, скорость, длина и ускорение, так как размерность ускорения может быть выражена с помощью скорости и длины (V2/L).

Вмеханике имеются три независимые величины. Так, для СИ независимыми являются длина L (метр), время Т (секунда) и масса М (килограмм).

Остальные величины являются производными, выражающимися через независимые в виде степенного одночлена 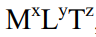, где х, у, z — алгебраические числа.

Пусть из каких-либо соображений или опытных исследований получена физическая зависимость в виде

а = f(а1,а2,…,аk,…, an)

где а1,а2,…,аk,…, an — численные, зависящие от единиц измерения значения некоторых функций, первые k из которых независимы. Примем их за характерные размеры. Если структура функции f выражает собой закон, не зависящий от выбора системы единиц измерения, то ее можно привести к виду

π = f(1,1,1,…,π1, π2, …, πn-k) (2.71)

Этот результат, именуемый π-теоремой, утверждает (доказательство опускаем), что функциональная связь между n + 1 размерными величинами а1,а2,…,аk,…, an, независимая от выбора системы единиц измерения, имеет вид соотношения между n + 1 - k безразмерными комбинациями из n + 1 безразмерной величины. Число единиц (1,1, ...) в (2.71) равно k.

В качестве второго примера применения π-теоремы приведем формулу Дарси (9.1) потерь напора в трубах, приняв сопротивления, приходящиеся на единицу длины трубы, в виде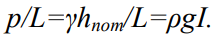

Теоретические и опытные данные подсказывают для этой формулы следующий вид:

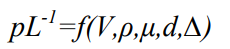(2.72)

где V - средняя скорость жидкости в сечении трубы; L — длина трубы; ∆ — шероховатость стенок; ρ — плотность; μ — вязкость жидкости; I гидравлический уклон.

Здесь n = 5, k = 3; значит, безразмерных комплексов будет 5 + 1 — 3 = 3.

Примем из этих величин за независимые V,ρ,d. Тогда π = f(1, 1, 1, π1,π2), где

или

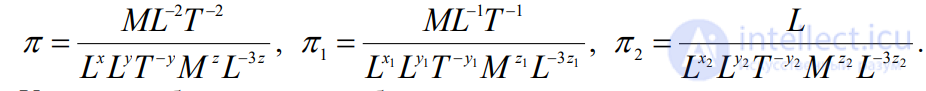
Условиями безразмерности будут:

для π

x + y −3z = −2, y = 2, z =1;

для π1

x1 + y1 −3z1 = −1, y1 =1, z1 =1;

для π2

x2 + y2 −3z2 =1, y2 = 0, z2 = 0;

Решая совместно эти три системы уравнений, находим:

x =1, y = 2, x1 = x2 = y1 = z = z1 =1, y2 = z2 = 0

Отсюда получаем

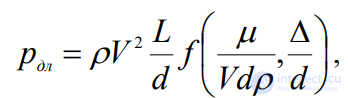
или формулу Дарси

Функция f (Re,∆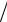d) = λ называется коэффициентом Дарси, см. формулу (3. ).

Исследование, описанное в статье про 8 Моделирование гидравлических процессов. Элементы теории размерностей, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 8 Моделирование гидравлических процессов. Элементы теории размерностей и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Гидромеханика, Гидравлика (Гидростатика, Гидродинамика)