ЛЕКЦИЯ 3 ОСНОВЫ ГИДРОДИНАМИКИ

Привет, Вы узнаете о том , что такое ЛЕКЦИЯ 3 ОСНОВЫ ГИДРОДИНАМИКИ, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое ЛЕКЦИЯ 3 ОСНОВЫ ГИДРОДИНАМИКИ , настоятельно рекомендую прочитать все из категории Гидродинамика.

Гидродинамика – раздел гидравлики, в котором изучаются законы
движения жидкости и ее взаимодействие с неподвижными и подвижными
поверхностями.
Если отдельные частицы абсолютно твердого тела жестко связаны
между собой, то в движущейся жидкой среде такие связи отсутствуют.
Движение жидкости состоит из чрезвычайно сложного перемещения
отдельных молекул.

3.1. Основные понятия о движении жидкости

Живым сечением  (м2
) называют площадь поперечного сечения
потока, перпендикулярную к направлению течения. Например, живое
сечение трубы – круг (рис.3.1, б); живое сечение клапана – кольцо с
изменяющимся внутренним диаметром (рис.3.1, б).


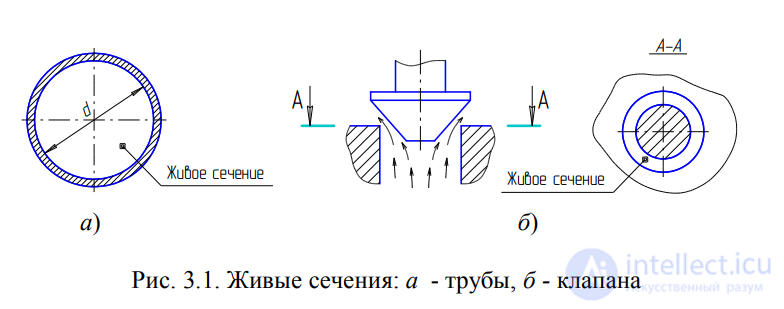
Рис. 3.1. Живые сечения: а - трубы, б - клапана

Смоченный периметр  («хи») - часть периметра живого сечения,
ограниченное твердыми стенками (рис.3.2, выделен утолщенной линией).

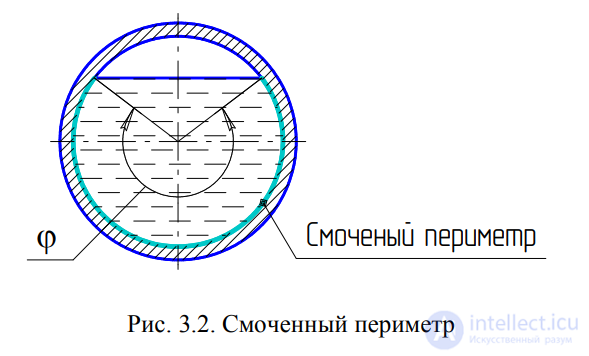
Рис. 3.2. Смоченный периметр

Для круглой трубы
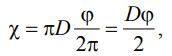если угол  в радианах,
или
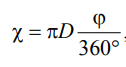, если угол  в градусах.
Расход потока Q – объем жидкости V, протекающей за единицу
времени t через живое сечение .
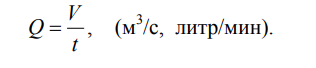. (3.1)
Средняя скорость потока  - скорость движения жидкости,
определяющаяся отношением расхода жидкости Q к площади живого
сечения 
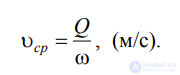. (3.2)
Поскольку скорость движения различных частиц жидкости
отличается друг от друга, поэтому скорость движения и усредняется. В
круглой трубе, например, скорость на оси трубы максимальна, тогда как у
стенок трубы она равна нулю.
Гидравлический радиус потока R – отношение живого сечения к
смоченному периметру
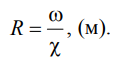, (м). (3.3)
Течение жидкости может быть установившимся и
неустановившимся. Установившимся движением называется такое
движение жидкости, при котором в данной точке русла давление и
скорость не изменяются во времени

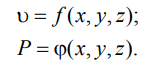
Движение, при котором скорость и давление изменяются не только
от координат пространства, но и от времени, называется
неустановившимся или нестационарным


Линия тока (применяется при неустановившемся движении) это
кривая, в каждой точке которой вектор скорости в данный момент времени
направлены по касательной.
Трубка тока – трубчатая поверхность, образуемая линиями тока с
бесконечно малым поперечным сечением. Часть потока, заключенная
внутри трубки тока называется элементарной струйкой.

Рис. 3.3. Линия тока

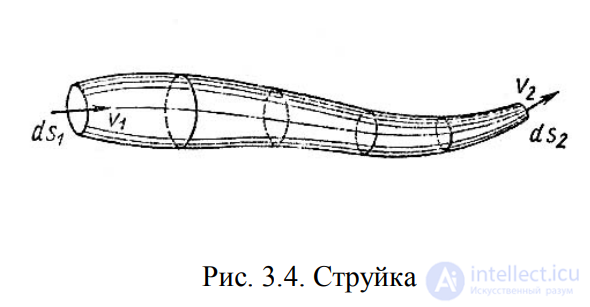
Рис. 3.4. Струйка

Течение жидкости может быть напорным и безнапорным. Напорное
течение наблюдается в закрытых руслах без свободной поверхности.
Напорное течение наблюдается в трубопроводах с повышенным
(пониженным давлением). Безнапорное - течение со свободной
поверхностью, которое наблюдается в открытых руслах (реки, открытые
каналы, лотки и т.п.). В данном курсе будет рассматриваться только
напорное течение.
Из закона сохранения вещества и постоянства расхода выводится
уравнение неразрывности течений. Об этом говорит сайт https://intellect.icu . Представим трубу с переменным
живым сечением (рис.3.5). Расход жидкости через трубу в любом ее
сечении постоянен, т.е. Q1  Q2 = const, откуда

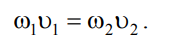
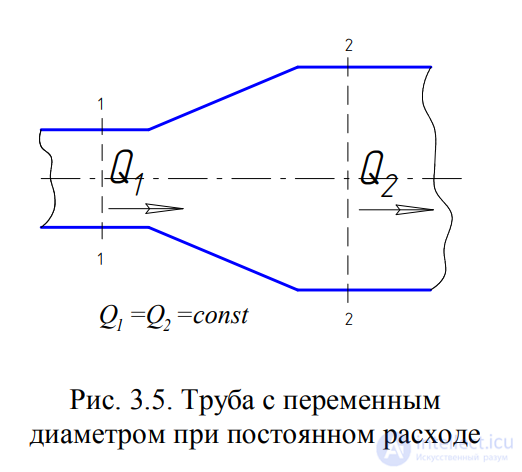
Рис. 3.5. Труба с переменным диаметром при постоянном расходе

.
Таким образом, если течение в
трубе является сплошным и
неразрывным, то уравнение
неразрывности примет вид:
(3.4)

3.2. Уравнение Бернулли для идеальной жидкости

Уравнение Даниила Бернулли, полученное в 1738 г., является
фундаментальным уравнением гидродинамики. Оно дает связь между
давлением P, средней скоростью  и пьезометрической высотой z в
различных сечениях потока и выражает закон сохранения энергии
движущейся жидкости. С помощью этого уравнения решается большой
круг задач.
Рассмотрим трубопровод переменного диаметра, расположенный в
пространстве под углом  (рис.3.6).

Рис.3.6. Схема к выводу уравнения Бернулли для идеальной жидкости

Выберем произвольно на рассматриваемом участке трубопровода два
сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого
сечения ко второму движется жидкость, расход которой равен Q.
Для измерения давления жидкости применяют пьезометры –
тонкостенные стеклянные трубки, в которых жидкость поднимается на
высоту

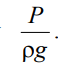
. В каждом сечении установлены пьезометры, в которых
уровень жидкости поднимается на разные высоты.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка,
загнутый конец которой направлен навстречу потоку жидкости, которая
называется трубка Питó. Жидкость в трубках Пито также поднимается на
разные уровни, если отсчитывать их от пьезометрической линии.
Пьезометрическую линию можно построить следующим образом.
Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров
и через показания уровней жидкости в них провести кривую, то мы
получим ломаную линию (рис.3.6).
Однако высота уровней в трубках Пито относительно произвольной
горизонтальной прямой 0-0, называемой плоскостью сравнения, будет
одинакова.
Если через показания уровней жидкости в трубках Пито провести
линию, то она будет горизонтальна, и будет отражать уровень полной
энергии трубопровода.
Для двух произвольных сечений 1-1 и 2-2 потока идеальной
жидкости уравнение Бернулли имеет следующий вид:
(3.5)
Так как сечения 1-1 и 2-2 взяты произвольно, то полученное
уравнение (3.5) можно переписать иначе:
(3.6)
и прочитать так: сумма трех членов уравнения Бернулли для любого
сечения потока идеальной жидкости есть величина постоянная.
С энергетической точки зрения каждый член уравнения представляет
собой определенные виды энергии:
z1 и z2 – удельные энергии положения, характеризующие
потенциальную энергию в сечениях 1-1 и 2-2;
- удельные энергии давления, характеризующие
потенциальную энергию давления в тех же сечениях;

- удельные кинетические энергии в тех же сечениях.

Следовательно, согласно уравнению Бернулли, полная удельная
энергия идеальной жидкости в любом сечении постоянна.
Уравнение Бернулли можно истолковать и чисто геометрически.
Дело в том, что каждый член уравнения имеет линейную размерность.
Глядя на рис.3.6, можно заметить, что z1 и z2 – геометрические высоты

сечений 1-1 и 2-2 над плоскостью сравнения;

- пьезометрические
высоты;

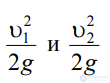
- скоростные высоты в указанных сечениях.

В этом случае уравнение Бернулли можно прочитать так: сумма
геометрической, пьезометрической и скоростной высоты для идеальной
жидкости есть величина постоянная.

3.3. Уравнение Бернулли для реальной жидкости

Уравнение Бернулли для потока реальной жидкости несколько
отличается от уравнения (3.5).
Дело в том, что при движении реальной вязкой жидкости возникают
силы трения, на преодоление которых жидкость затрачивает энергию. В
результате полная удельная энергия жидкости в сечении 1-1 будет больше
полной удельной энергии в сечении 2-2 на величину потерянной энергии
(рис.3.7).


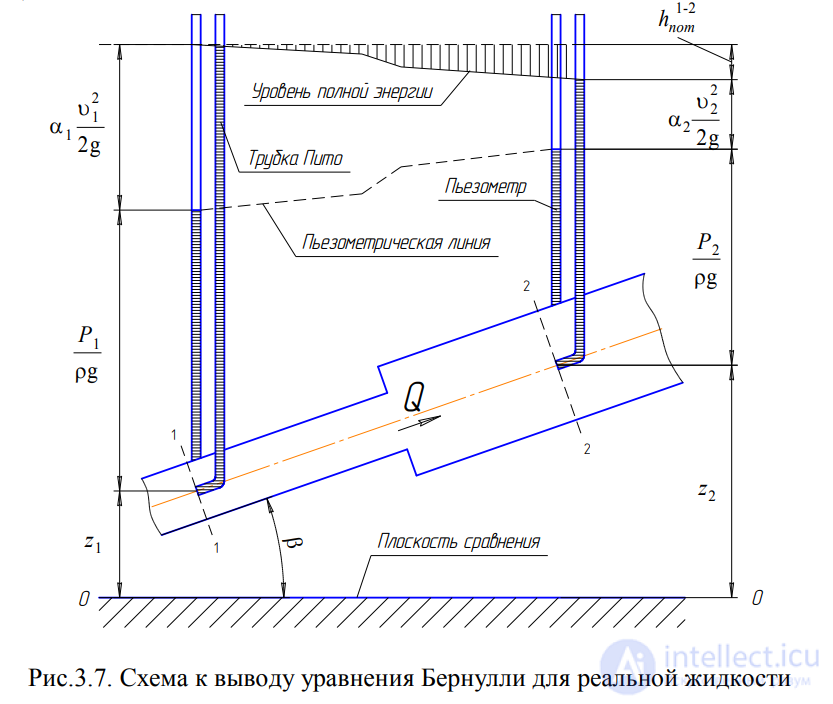
Рис.3.7. Схема к выводу уравнения Бернулли для реальной жидкости

Потерянная энергия или потерянный напор обозначаются 12 hпот и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:
(3.7)
Из рис.3.7 видно, что по мере движения жидкости от сечения 1-1 до
сечения 2-2 потерянный напор все время увеличивается (потерянный
напор выделен вертикальной штриховкой). Таким образом, уровень
первоначальной энергии, которой обладает жидкость в первом сечении,
для второго сечения будет складываться из четырех составляющих:
геометрической высоты, пьезометрической высоты, скоростной высоты и
потерянного напора между сечениями 1-1 и 2-2.
Кроме этого в уравнении появились еще два коэффициента 1 и 2,
которые называются коэффициентами Кориолиса и зависят от режима
течения жидкости ( = 2 для ламинарного режима,  = 1 – для
турбулентного режима1
).
Потерянная высота 12
hпот складывается из линейных потерь,
вызванных силой трения между слоями жидкости, и потерь, вызванных
местными сопротивлениями2
(изменениями конфигурации потока)
пот лин мест

.
С помощью уравнения Бернулли решается большинство задач
практической гидравлики. Для этого выбирают два сечения по длине
потока, таким образом, чтобы для одного из них были известны величины
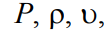а для другого сечения одна или величины подлежали определению.
При двух неизвестных для второго сечения используют уравнение
постоянства расхода жидкости

3.4. Измерение скорости потока и расхода жидкости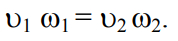

Для измерения скорости в точках потока широко используется
работающая на принципе уравнения Бернулли трубка Пито (рис.3.8),
загнутый конец которой направлен навстречу потоку. Пусть требуется
измерить скорость жидкости в какой-то точке потока. Поместив конец
трубки в указанную точку и составив уравнение Бернулли для сечения I-I и
сечения, проходящего на уровне жидкости в трубке Пито получим

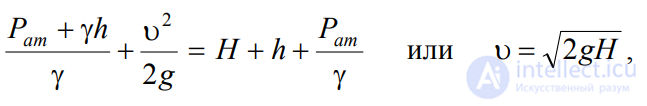
1 Режимы движения жидкости рассмотрены в лекции №4
2 Местные сопротивления трубопроводов рассмотрены в лекции №4

где Н – столб жидкости в трубке Пито.

Рис. 3.8. Трубка Пито Рис. 3.9. Расходомер Вентури
Для измерения расхода жидкости в трубопроводах часто используют
расходомер Вентури, действие которого основано так же на принципе
уравнения Бернулли. Расходомер Вентури состоит из двух конических
насадков с цилиндрической вставкой между ними (рис.3.9). Если в
сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет
зависеть от расхода жидкости, протекающей по трубе.
Пренебрегая потерями напора и считая z1 = z2 , напишем уравнение
Бернулли для сечений I-I и II-II:

или

Используя уравнение неразрывности

,
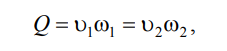
сделаем замену в полученном выражении:

Решая относительно Q, получим


.
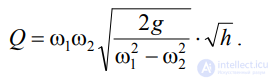
Выражение, стоящее перед h , является постоянной величиной,
носящей название постоянной водомера Вентури.
Из полученного уравнения видно, что h зависит от расхода Q. Часто
эту зависимость строят в виде тарировочной кривой h от Q, которая имеет
параболический характер

Исследование, описанное в статье про ЛЕКЦИЯ 3 ОСНОВЫ ГИДРОДИНАМИКИ, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое ЛЕКЦИЯ 3 ОСНОВЫ ГИДРОДИНАМИКИ и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Гидродинамика