ЛЕКЦИЯ 2 ОСНОВЫ ГИДРОСТАТИКИ

Привет, Вы узнаете о том , что такое ЛЕКЦИЯ 2 ОСНОВЫ ГИДРОСТАТИКИ, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое ЛЕКЦИЯ 2 ОСНОВЫ ГИДРОСТАТИКИ , настоятельно рекомендую прочитать все из категории Гидромеханика, Гидростатика, Гидродинамика.

Гидравлика делится на два раздела: гидростатика и гидродинамика.

Гидростатика — раздел физики сплошных сред, изучающий равновесие жидкостей (в частности, в поле тяжести).

Гидростатика — это теория поведения неподвижных жидкостей.

При изучении гидростатики возможно провести некоторые аналогии с теорией упругости, изучающей равновесие твердых тел; при этом, в отличие от твердого тела, жидкость не оказывает сопротивления сдвиговым напряжениям. Именно поэтому в жидкости не может существовать анизотропии напряжений. Следовательно, вместо многокомпонентного тензора (для твердого тела), напряжения в жидкости описываются единственной величиной — давлением. Отсюда вытекает закон Паскаля: давление, оказываемое на жидкость, передается жидкостью одинаково во всех направлениях.

Гидродинамика является более обширным разделом и будет рассмотрена в
последующих лекциях. В этой лекции будет рассмотрена гидростатика.
Гидростатикой называется раздел гидравлики, в котором
рассматриваются законы равновесия жидкости и их практическое
применение.

Основные положения:

• Закон Паскаля: давление в жидкости передается во все стороны одинаково.

• Закон Архимеда: на всякое тело, погруженное в жидкость, действует выталкивающая сила.

• Давление увеличивается с глубиной: p=ρgh

Некоторые принципы гидростатики были известны в эмпирическом и интуитивном смысле еще со времен античности, строителям лодок, цистерн , акведуков и фонтанов . Архимеду приписывают открытие принципа Архимеда , который связывает выталкивающую силу, действующую на объект, погруженный в жидкость, с весом жидкости, вытесненной объектом. Римский инженер Витрувий предупреждал читателей о том, что свинцовые трубы могут лопнуть под действием гидростатического давления.

Понятие давления и способ его передачи жидкостями были сформулированы французским математиком и философом Блезом Паскалем в 1647 году .

Таблица гидравлики и гидростатики из «Энциклопедии» 1728 года

«Честная чаша» или пифагорейская чаша , которая датируется примерно 6 веком до нашей эры, является гидравлической технологией, изобретение которой приписывают греческому математику и геометру Пифагору. Она использовалась в качестве учебного пособия.

Чашка состоит из линии, вырезанной внутри чашки, и небольшой вертикальной трубы в центре чашки, которая ведет к дну. Высота этой трубы такая же, как и линия, вырезанная внутри чашки. Чашка может быть заполнена до линии без попадания жидкости в трубу в центре чашки. Однако, когда количество жидкости превышает эту линию заполнения, жидкость перельется в трубу в центре чашки. Из-за сопротивления, которое молекулы оказывают друг на друга, чашка опустеет.

Фонтан Герона — это устройство, изобретенное Героном Александрийским , которое представляет собой струю жидкости, питаемую резервуаром с жидкостью. Фонтан сконструирован таким образом, что высота струи превышает высоту жидкости в резервуаре, по-видимому, в нарушение принципов гидростатического давления. Устройство состояло из отверстия и двух контейнеров, расположенных один над другим. Промежуточный горшок, который был запечатан, был заполнен жидкостью, и нескольких канюль (небольшая трубка для передачи жидкости между сосудами), соединяющих различные сосуды. Захваченный внутри сосудов воздух вызывает струю воды из сопла, опорожняя всю воду из промежуточного резервуара.

Паскаль внес вклад в развитие как гидростатики, так и гидродинамики. Закон Паскаля является фундаментальным принципом механики жидкости, который гласит, что любое давление, приложенное к поверхности жидкости, передается равномерно по всей жидкости во всех направлениях таким образом, что начальные изменения давления не изменяются.

2.1. Гидростатическое давление

В покоящейся жидкости всегда присутствует сила давления, которая
называется гидростатическим давлением. Жидкость оказывает силовое
воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в
верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы
жидкости, находящиеся у дна.
Рассмотрим резервуар с плоскими вертикальными стенками,
наполненный жидкостью (рис.2.1, а). На дно резервуара действует сила P
равная весу налитой жидкости G =  V, т.е. P = G.
Если эту силу P разделить на площадь дна Sabcd, то мы получим
среднее гидростатическое давление, действующее на дно резервуара
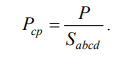(2.1)
Гидростатическое давление обладает свойствами.
Свойство 1. В любой точке жидкости гидростатическое давление
перпендикулярно площадке касательной к выделенному объему и
действует внутрь рассматриваемого объема жидкости.
Для доказательства этого утверждения вернемся к рис.2.1, а.
Выделим на боковой стенке резервуара площадку Sбок (заштриховано).
Гидростатическое давление действует на эту площадку в виде
распределенной силы, которую можно заменить одной равнодействующей,
которую обозначим P. Предположим, что равнодействующая
гидростатического давления P, действующая на эту площадку, приложена
в точке А и направлена к ней под углом  (на рис. 2.1 обозначена
штриховым отрезком со стрелкой). Тогда сила реакции стенки R на
жидкость будет иметь ту же самую величину, но противоположное
направление (сплошной отрезок со стрелкой). Указанный вектор R можно

разложить на два составляющих вектора: нормальный Rn
(перпендикулярный к заштрихованной площадке) и касательный R к
стенке.

Рис. 2.1. Схема, иллюстрирующая свойства гидростатического давления
а – первое свойство; б – второе свойство
Сила нормального давления Rn вызывает в жидкости напряжения
сжатия. Этим напряжениям жидкость легко противостоит. Сила R ,
действующая на жидкость вдоль стенки, должна была бы вызвать в
жидкости касательные напряжения вдоль стенки и частицы должны были
бы перемещаться вниз. Об этом говорит сайт https://intellect.icu . Но так как жидкость в резервуаре находится в
состоянии покоя, то составляющая R отсутствует. Отсюда можно сделать
вывод первого свойства гидростатического давления.
Свойство 2. Гидростатическое давление неизменно во всех
направлениях.
В жидкости, заполняющей какой-то резервуар, выделим
элементарный1
кубик с очень малыми сторонами x, y, z (рис.2.1, б). На
каждую из боковых поверхностей будет давить сила гидростатического
давления, равная произведению соответствующего давления Px, Py, Pz на
элементарные площади. Обозначим вектора давлений, действующие в
положительном направлении (согласно указанным координатам) как Px ,Py , Pz, а вектора давлений, действующие в обратном направлении1
Термин «элементарный» означает очень маленькое значение, которое стремится приблизиться к нулю.
В данном случае это линейный размер сторон кубика.

соответственно Поскольку кубик находится в равновесии, то
можно записать равенства

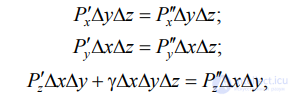
где γ - удельный вес жидкости;
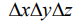– объем кубика.
Сократив полученные равенства, найдем, что

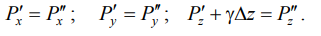
Членом третьего уравнения z, как бесконечно малым по сравнению с
Pz
 и Pz
 , можно пренебречь и тогда окончательно

Вследствие того, что кубик не деформируется (не вытягивается
вдоль одной из осей), надо полагать, что давления по различным осям
одинаковы, т.е.
. (2.2)
Это доказывает второй свойство гидростатического давления.

Свойство 3. Гидростатическое давление в точке зависит от ее
координат в пространстве.
Это положение не требует специального доказательства, так как
ясно, что по мере увеличения погружения точки давление в ней будет
возрастать, а по мере уменьшения погружения уменьшаться. Третье
свойство гидростатического давления может быть записано в виде

2.2. Основное уравнение гидростатики

Рассмотрим распространенный случай равновесия жидкости, когда
на нее действует только одна массовая сила – сила тяжести, и получим
уравнение, позволяющее находить гидростатическое давление в любой
точке рассматриваемого объема жидкости. Это уравнение называется
основным уравнением гидростатики.
Пусть жидкость содержится в сосуде (рис.2.2) и на ее свободную
поверхность действует давление P0. Найдем гидростатическое давление P
в произвольно взятой точке М, расположенной на глубине h. Выделим
около точки М элементарную горизонтальную площадку dS и построим на
ней вертикальный цилиндрический объем жидкости высотой h.
Рассмотрим условие равновесия указанного объема жидкости,
выделенного из общей массы жидкости. Давление жидкости на нижнее
основание цилиндра теперь будет внешним и направлено по нормали
внутрь объема, т.е. вверх.

Рис. 2.2. Схема для вывода основного уравнения гидростатики
Запишем сумму сил,
действующих на рассматриваемый
объем в проекции на
вертикальную ось:

Последний член уравнения
представляет собой вес жидкости,
заключенный в рассматриваемом
вертикальном цилиндре объемом
h dS. Силы давления по боковой
поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к
этой поверхности и их проекции на вертикальную ось равны нулю.
Сократив выражение на dS и перегруппировав члены, найдем
. (2.3)
Полученное уравнение называют основным уравнением
гидростатики. По нему можно посчитать давление в любой точке
покоящейся жидкости. Это давление, как видно из уравнения,
складывается из двух величин: давления P0 на внешней поверхности
жидкости и давления, обусловленного весом вышележащих слоев
жидкости.
Из основного уравнения гидростатики видно, что какую бы точку в
объеме всего сосуда мы не взяли, на нее всегда будет действовать
давление, приложенное к внешней поверхности P0. Другими словами
давление, приложенное к внешней поверхности жидкости, передается всем
точкам этой жидкости по всем направлениям одинаково. Это положение
известно под названием закона Паскаля.
Поверхность, во всех точках которой давление одинаково,
называется поверхностью уровня (подробно рассмотрим в п.2.6). В
обычных условиях поверхности уровня представляют собой
горизонтальные плоскости.

2.3. Давление жидкости на плоскую наклонную стенку

Пусть мы имеем резервуар с наклонной правой стенкой,
заполненный жидкостью с удельным весом . Ширина стенки в
направлении, перпендикулярном плоскости чертежа (от читателя), равна b
(рис.2.3). Стенка условно показана развернутой относительно оси АВ и
заштрихована на рисунке. Построим график изменения избыточного
гидростатического давления на стенку АВ.
Так как избыточное гидростатическое давление изменяется по
линейному закон P=gh, то для построения графика, называемого эпюрой
давления, достаточно найти давление в двух точках, например А и B.

Рис. 2.3. Схема к определению равнодействующей гидростатического
давления на плоскую поверхность
Избыточное гидростатическое давление в точке А будет равно

.
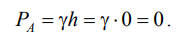
Соответственно давление в точке В:

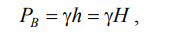
где H – глубина жидкости в резервуаре.
Согласно первому свойству гидростатического давления, оно всегда
направлено по нормали к ограждающей поверхности. Следовательно,

гидростатическое давление в точке В, величина которого равна H, надо
направлять перпендикулярно к стенке АВ. Соединив точку А с концом
отрезка H, получим треугольную эпюру распределения давления АВС с
прямым углом в точке В. Среднее значение давления будет равно
. (2.4)
Если площадь наклонной стенки S=bL, то равнодействующая
гидростатического давления равна
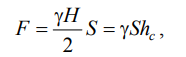, (2.5)
где hc = Н/2 – глубина погружения центра тяжести плоской поверхности
под уровень жидкости.
Однако точка приложения равнодействующей гидростатического
давления ц.д. не всегда будет совпадать с центром тяжести плоской
поверхности. Эта точка находится на расстоянии  от центра тяжести и
равна отношению момента инерции площадки относительно центральной
оси к статическому моменту этой же площадки.
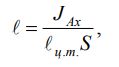, (2.6)
где J Аx – момент инерции площади S относительно центральной оси,
параллельной Аx.
В частном случае, когда стенка имеет форму прямоугольника
размерами bL и одна из его сторон лежит на свободной поверхности с
атмосферным давлением, центр давления ц.д. находится на расстоянии b/3
от нижней стороны.

2.4. Давление жидкости на цилиндрическую поверхность

Пусть жидкость заполняет резервуар, правая стенка которого
представляет собой цилиндрическую криволинейную поверхность АВС
(рис.2.4), простирающуюся в направлении читателя на ширину b.
Восстановим из точки А перпендикуляр АО к свободной поверхности
жидкости. Объем жидкости в отсеке АОСВ находится в равновесии. Это
значит, что силы, действующие на поверхности выделенного объема V, и
силы веса взаимно уравновешиваются.

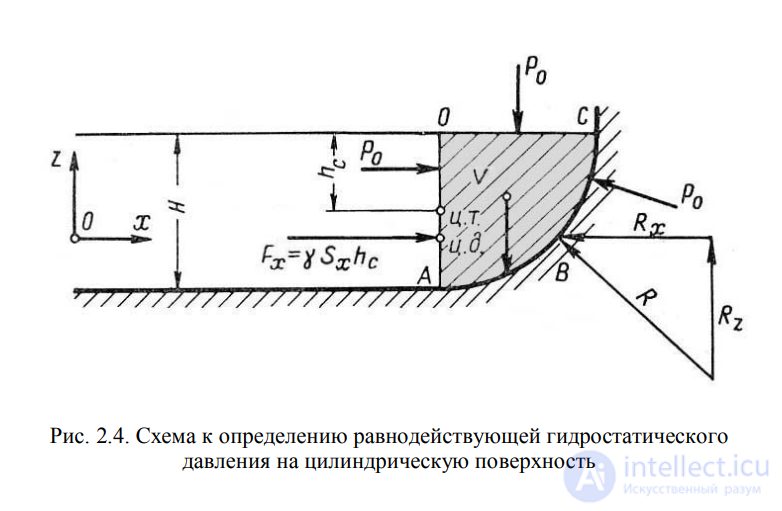
Рис. 2.4. Схема к определению равнодействующей гидростатического
давления на цилиндрическую поверхность
Представим, что выделенный объем V представляет собой твердое
тело того же удельного веса, что и жидкость (этот объем на рис.2.4
заштрихован). Левая поверхность этого объема (на чертеже вертикальная
стенка АО) имеет площадь Sx = bH, являющуюся проекцией
криволинейной поверхности АВС на плоскость yOz.
Из уравнения (2.5) сила гидростатического давления на площадь Sx
равна x x c F  S h .
С правой стороны на отсек будет действовать реакция R
цилиндрической поверхности. Пусть точка приложения и направление
этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим
на две составляющие Rx и Rz
.
Из действующих поверхностных сил осталось учесть только
давление на свободной поверхности Р0. Если резервуар открыт, то
естественно, что давление Р0 одинаково со всех сторон и поэтому взаимно
уравновешивается.
На отсек АВСО будет действовать сила собственного веса G = V,
направленная вниз.
Спроецируем все силы на ось Ох:
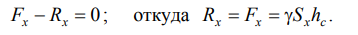. (2.7)
Теперь спроецируем все силы на ось Оz:
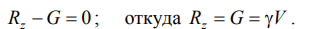. (2.8)
Составляющая силы гидростатического давления по оси Oy
обращается в нуль, значит Ry = Fy = 0.

Таким образом, реакция цилиндрической поверхности в общем
случае равна

,
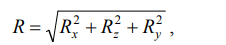
а поскольку реакция цилиндрической поверхности равна
равнодействующей гидростатического давления R=F, то делаем вывод, что
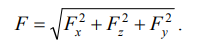. (2.9)

2.5. Закон Архимеда и его приложение

Тело, погруженное (полностью или частично) в жидкость,
испытывает со стороны жидкости суммарное давление, направленное
снизу вверх и равное весу жидкости в объеме погруженной части тела.
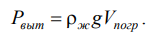. (2.10)
Для однородного тела плавающего на поверхности справедливо
соотношение

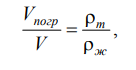
где: V – объем плавающего тела;
т – плотность тела.
Существующая теория плавающего тела довольно обширна, поэтому
мы ограничимся рассмотрением лишь гидравлической сущности этой
теории.
Способность плавающего тела, выведенного из состояния
равновесия, вновь возвращаться в это состояние называется
остойчивостью. Вес жидкости, взятой в объеме погруженной части судна
называют водоизмещением, а точку приложения равнодействующей
давления (т.е. центр давления) – центром водоизмещения. При
нормальном положении судна центр тяжести С и центр водоизмещения d
лежат на одной вертикальной прямой O  O , представляющей ось
симметрии судна и называемой осью плавания (рис.2.5).
Пусть под влиянием внешних сил судно наклонилось на некоторый
угол , часть судна KLM вышла из жидкости, а часть KLM , наоборот,
погрузилось в нее. При этом получили новое положении центра
водоизмещения d. Приложим к точке d подъемную силу R и линию ее
действия продолжим до пересечения с осью симметрии O  O .
Полученная точка m называется метацентром, а отрезок mC = h

называется метацентрической высотой. Будем считать h положительным,
если точка m лежит выше точки C, и отрицательным – в противном случае.

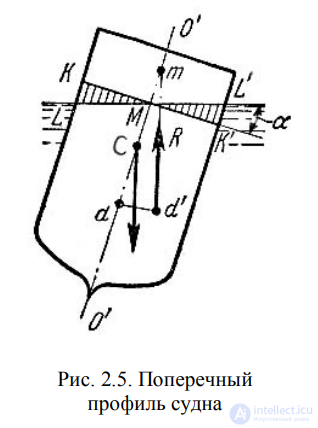
Рис. 2.5. Поперечный профиль судна

Теперь рассмотрим условия
равновесия судна:
1) если h > 0, то судно
возвращается в первоначальное
положение;
2) если h = 0, то это случай
безразличного равновесия;
3) если h < 0, то это случай
неостойчивого равновесия, при
котором продолжается дальнейшее
опрокидывание судна.
Следовательно, чем ниже
расположен центр тяжести и, чем
больше метацентрическая высота,
тем больше будет остойчивость
судна.

2.6. Поверхности равного давления

Как уже отмечалось выше, поверхность, во всех точках которой
давление одинаково, называется поверхностью уровня или поверхностью
равного давления. При неравномерном или непрямолинейном движении на
частицы жидкости кроме силы тяжести действуют еще и силы инерции,
причем если они постоянны по времени, то жидкость принимает новое
положение равновесия. Такое равновесие жидкости называется
относительным покоем.
Рассмотрим два примера такого относительного покоя.
В первом примере определим поверхности уровня в жидкости,
находящейся в цистерне, в то время как цистерна движется по
горизонтальному пути с постоянным ускорением a (рис.2.6).

Рис. 2.6. Движение цистерны с ускорением
К каждой частице жидкости
массы m должны быть в этом случае
приложены ее вес G = mg и сила
инерции Pи, равная по величине ma.
Равнодействующая этих сил

направлена к вертикали под углом ,
тангенс которого равен

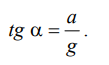
Так как свободная поверхность, как поверхность равного давления,
должна быть нормальна к указанной равнодействующей, то она в данном
случае представит собой уже не горизонтальную плоскость, а наклонную,
составляющую угол  с горизонтом. Учитывая, что величина этого угла
зависит только от ускорений, приходим к выводу, что положение
свободной поверхности не будет зависеть от рода находящейся в цистерне
жидкости. Любая другая поверхность уровня в жидкости также будет
плоскостью, наклоненной к горизонту под углом . Если бы движение
цистерны было не равноускоренным, а равнозамедленным, направление
ускорения изменилось бы на обратное, и наклон свободной поверхности
обратился бы в другую сторону (см. рис.2.6, пунктир).
В качестве второго примера рассмотрим часто встречающийся в
практике случай относительного покоя жидкости во вращающихся сосудах
(например, в сепараторах и центрифугах, применяемых для разделения
жидкостей). В этом случае (рис.2.7) на любую частицу жидкости при ее
относительном равновесии действуют массовые силы: сила тяжести
G = mg и центробежная сила Pи = m2r, г

де r – расстояние частицы от оси
вращения, а  - угловая скорость вращения сосуда. Поверхность жидкости

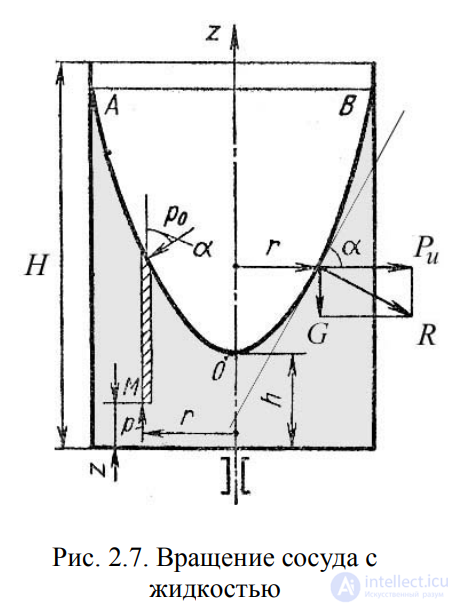
Рис. 2.7. Вращение сосуда с жидкостью
также должна быть нормальна в
каждой точке к равнодействующей
этих сил R и представит собой
параболоид вращения.
Из чертежа находим

С другой стороны:

где z – координата рассматриваемой
точки. Таким образом, получаем:

,
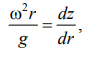
откуда


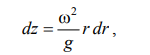
или после интегрирования

.
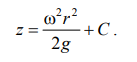
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C,
поэтому окончательно будем иметь
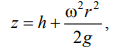, (2.11)
т.е. кривая АОВ является параболой, а свободная поверхность жидкости
параболоидом. Такую же форму имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся
жидкости в функции радиуса и высоты выделим вертикальный
цилиндрический объем жидкости с основанием в виде элементарной
горизонтальной площадки dS (точка М) на произвольном радиусе r и
высоте z и запишем условие его равновесия в вертикальном направлении.
С учетом уравнения (2.11) будем иметь

.
После сокращений получим

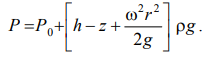. (2.12)
Это значит, что давление возрастает пропорционально радиусу r и
уменьшается пропорционально высоте z

Применение гидростатики:

• Проектирование водохранилищ, плотин.

• Гидравлические подъемники.

• Расчет давления на подводные конструкции.

• Навигация (плавание судов, подводных лодок).

• Сообщающиеся сосуды – набор сообщающихся внутри емкостей, содержащих однородную жидкость.
• Гидростатическое испытание – Неразрушающий контроль сосудов высокого давления
• D-DIA – Аппарат, используемый для экспериментов по деформации при высоком давлении и высокой температуре.

Исследование, описанное в статье про ЛЕКЦИЯ 2 ОСНОВЫ ГИДРОСТАТИКИ, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое ЛЕКЦИЯ 2 ОСНОВЫ ГИДРОСТАТИКИ и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Гидромеханика, Гидростатика, Гидродинамика