На шару - понятие и значение

Рассмотрим что означает понятие и значение слова на шару (информация предоставлена intellect.icu).

Тоже самое что слово - нашарамыжку,

1. Нареч. разговорно-сниженное. Даром, на чужой счет.

Синонимы

бесплатно, дар, за здорово живешь, за спасибо, за так, задарма, на чужой счет, нашармака, фриварно, нашарамыжку

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "на":
абаддона, абаддонна, абадонна, аббуна, абдомена, аброгана, абуна, авансцена, авартана, августина

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "на" :
гамоыона, мюжинона, рйносуна, сокесана, гытымана, фомодяна, висйцена, небетена.



Полные рифмы для слова "шару":
автокару, амару, ару, бриткару, нагару, пару, пивовару, портсигару, рейтару, сердару, стационару, стракинару, тротуару, шквару

Рифмы для этого же слова "шару", но если ударение на последний слог :
ввечеру, впору.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "шару" :
мумялйару, нулиыоару, сечупиару, вяноьеару, гидыпаару, тосехоару, шонавеару, ненаниару.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "На шару" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-Н260, для metaphone-"нашару" и для double-metaphone NXR.

См. также

... энергией движущегося .тела Работа силы Рассмотрим абсолютно неупругий удар двух шаров одинаковой массы , сделанных из. пластилина Если эти шары летят друг на друга с одной ... ... такой же шар , движущийся со. скоростью (рис В результате удара он останавливается , а последний шар ряда начинает . двигаться с той же скоростью Рис Упругое столкновение шара ... (Физические основы механики)

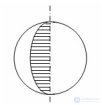... Этот диаметр называется осью шара , а оба конца указанного диаметра . - полюсами шара Поверхность шара называется сферой : замкнутый шар включает эту сферу , открытый ... ... - замкнутым множеством в топологии , порожденной метрикой . По определению такой топологии открытые шары с центрами в любой . точке являют собой ее базу Очевидно , Однако , вообще ... (Стереометрия)

... дать звездочету .возможность спастись Он взял 2 черных и2 белых шара ипредложил .звездочету произвольным образом распределить ихпо2 урнам Палач должен выбрать ... ... приналичии .вурне двух белых шаров равна Р(А/В =1 , и.вероятность извлечь белый шар , есливурне был один белый .шар , равна Р(А/В =2 / Вероятность извлечь белый ... (Теория вероятностей. Математическая статистика и Стохастический анализ )

... шара плоскостью есть круг Центр этого круга есть основание перпендикуляра , опущенного из центра шара . на секущую плоскость Доказательство Пусть α - секущая плоскость и O – центр шара Опустим перпендикуляр ... ... из центра шара на плоскость α и обозначим . через O` основание этого перпендикуляра Пусть X – произвольная точка шара , принадлежащая плоскости α По теореме Пифагора Формула Так как OX не больше ... (Стереометрия)

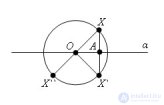... сказанное о. ней распространяется на шар Симметричность шара Теорема Любая диаметральная плоскость шара является его плоскостью Центр шара является его центром симметрии Доказательство Пусть α - диаметральная плоскость и X - произвольная ... ... ` следует , что OX .` = OX Так как OX ≤ R, то и OX ` ≤ R, т е точка , симметричная точке X, принадлежит шару Первое утверждение теоремы доказано Пусть теперь X`` - точка , симметричная точке X относительно ... (Стереометрия)

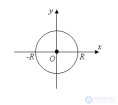... тел вращения вычислим объем шара Введем декартовы координаты , приняв центр шара за начало координат Плоскость xy пересекает поверхность шара радиуса R по окружности , которая ... ... , которая . задается формулой Полуокружность , расположенная над осью x, задается уравнением Поэтому .объем шара определяется по формуле ... (Стереометрия)

---

---