1. Разговорное.2. Уменьшительно ласкательное существительное: барельеф.3. Ласкательное существительное: барельеф.

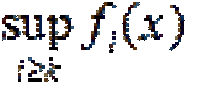 ... , содержащую все открытые множества t Напомним (определение , что множества А, принадлежащие этой , называются борелевскими . Так как дополнение открытого множества является замкнутым , то все открытые . и замкнутые множества являются ... ... . Так как дополнение открытого множества является замкнутым , то все открытые . и замкнутые множества являются борелевскими В том числе все промежутки на прямой (отрезки , интервалы и. полуинтервалы ) являются борелевскими множествами ... (Функциональный анализ)
... , содержащую все открытые множества t Напомним (определение , что множества А, принадлежащие этой , называются борелевскими . Так как дополнение открытого множества является замкнутым , то все открытые . и замкнутые множества являются ... ... . Так как дополнение открытого множества является замкнутым , то все открытые . и замкнутые множества являются борелевскими В том числе все промежутки на прямой (отрезки , интервалы и. полуинтервалы ) являются борелевскими множествами ... (Функциональный анализ)
 ... . (пишем (S, Й§) ~ (V, si )), если существует взаимно-однозначное отображение h: S У V такое , что h G Зе \ sd . и Н±г G sd \ ё&. Если V - борелевское подмножество отрезка [0, сг-алгебраборелевскихподмножеств V (т. е «с/ = ([0, ), то изоморфное ему пространство (S, Ж) называется . борелевским пространством Напомним ... ... , будет пространство Ет с евклидовой метрикой Известно (см , например , [41 ; том , что любое борелевское подмножество польского пространства с. сг-алгеброй своих борелевских подмножеств является борелевским пространством Теорема ... (вероятностные процессы)
... . (пишем (S, Й§) ~ (V, si )), если существует взаимно-однозначное отображение h: S У V такое , что h G Зе \ sd . и Н±г G sd \ ё&. Если V - борелевское подмножество отрезка [0, сг-алгебраборелевскихподмножеств V (т. е «с/ = ([0, ), то изоморфное ему пространство (S, Ж) называется . борелевским пространством Напомним ... ... , будет пространство Ет с евклидовой метрикой Известно (см , например , [41 ; том , что любое борелевское подмножество польского пространства с. сг-алгеброй своих борелевских подмножеств является борелевским пространством Теорема ... (вероятностные процессы)
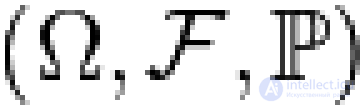 ... удовлетворяет следующим трем свойствам .: — функция неубывающая ; ; непрерывна справа Из того факта , что борелевская сигма-алгебра на вещественной прямой порождается . семейством интервалов вида , вытекает Теорема Любая ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... удовлетворяет следующим трем свойствам .: — функция неубывающая ; ; непрерывна справа Из того факта , что борелевская сигма-алгебра на вещественной прямой порождается . семейством интервалов вида , вытекает Теорема Любая ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... Польскими пространствами называются полные сепарабельные метрические пространства Мы будем рассматривать борелевские вероятностные меры на польском пространстве X., то есть, меры , определенные на борелевской σ-алгебре B(X). Метрику X будем обозначать ... ... µn({f(x) > t}) dt =. µ({f (x) > t}) dt = f (x) dµ n n 0 0 □ Следующий факт известен как теорема Улама Теорема Пусть µ вероятностная борелевская мера на польском пространстве X. Для любого ε > 0 существует такое компактное множество K ⊂ X, что. µ(X \ K) ≤ ε Доказательство ... (вероятностные процессы)
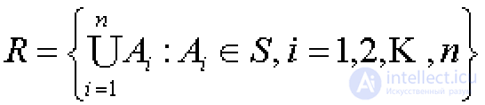 ... превосходит e/ Тогда m*(А) £ e В силу теоремы 11 это означает , что множество А измеримо . и имеет меру Определение Борелевскими множествами называют множества , принадлежащие наименьшей множеств , содержащей . все открытые и замкнутые ... ... . измеримы , а все измеримые множества образуют , то очевидна следующая .теорема Теорема Все борелевские множества из Rn измеримы Теорема Внешняя мера любого множества Е Ì Rn равна ... (Функциональный анализ)
... превосходит e/ Тогда m*(А) £ e В силу теоремы 11 это означает , что множество А измеримо . и имеет меру Определение Борелевскими множествами называют множества , принадлежащие наименьшей множеств , содержащей . все открытые и замкнутые ... ... . измеримы , а все измеримые множества образуют , то очевидна следующая .теорема Теорема Все борелевские множества из Rn измеримы Теорема Внешняя мера любого множества Е Ì Rn равна ... (Функциональный анализ)
 ... следующее :. Характеристическая функция Пусть векторная случайная величина в мерном действительном пространстве , где борелевская . алгебра Функция переменной , называется функцией распределения случайной величины ( или функцией совместного ... ... различная терминология для различных представлений теоремы . Байеса Функции от случайных величин Если - борелевская функция , а - случайная величина , то ее функциональное преобразование . также является случайной величиной Например , если - стандартная ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... следующее :. Характеристическая функция Пусть векторная случайная величина в мерном действительном пространстве , где борелевская . алгебра Функция переменной , называется функцией распределения случайной величины ( или функцией совместного ... ... различная терминология для различных представлений теоремы . Байеса Функции от случайных величин Если - борелевская функция , а - случайная величина , то ее функциональное преобразование . также является случайной величиной Например , если - стандартная ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
Комментарии
Оставить комментарий