Лекция
Привет, мой друг, тебе интересно узнать все про аппроксимация функций, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое аппроксимация функций, интерполяция , интерполяция функций, аппроксимация, интерполирование, непрерывная аппроксимация, точечная аппроксимация, интерполяционный полином лагранжа, интерполяционный полином ньютона, погрешность глобальной интерполяции, метод наименьших квадратов, подбор эмпирических формул, кусочно-постоянная интерполяция, кусочно-линейная интерполяция , настоятельно рекомендую прочитать все из категории Численные методы.
Аппроксимировать – это означает "приближенно заменять". Допустим, известны значения некоторой функции в заданных точках. Требуется найти промежуточные значения этой функции. Это так называемая задача о восстановлении функции. Кроме того, при проведении расчетов сложные функции удобно заменять алгебраическими многочленами или другими элементарными функциями, которые достаточно просто вычисляются (задача о приближении функции).
интерполяция — это метод нахождения неизвестных промежуточных значений некоторой функции по имеющемуся дискретному набору ее известных значений. Типичным примером такой функции является временной ряд, значения которого — это наблюдения, зафиксированные через определенный интервал времени.
Интерполяция, интерполирование (от лат. inter–polis — «разглаженный, подновленный, обновленный; преобразованный») — в вычислительной математике нахождение неизвестных промежуточных значений некоторой функции, по имеющемуся дискретному набору ее известных значений, определенным способом. Термин «интерполяция» впервые употребил Джон Валлис в своем трактате «Арифметика бесконечных» (1656).
В функциональном анализе интерполяция линейных операторов представляет собой раздел, рассматривающий банаховы пространства как элементы некоторой категории .
Отличие апроксимации от интерполяции.
Интерпояция — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
аппроксимация , или приближение — математический метод, состоящий в замене одних математических объектов другими, в том или ином смысле близкими к исходным, но более простыми.
В научных и инженерных расчетах, часто приходится оперировать наборами значений, полученных опытным путем или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.
Существует также близкая к интерполяции задача, которая заключается в аппроксимации какой-либо сложной функции другой, более простой функцией. Если некоторая функция слишком сложна для производительных вычислений, можно попытаться вычислить ее значение в нескольких точках, а по ним построить, то есть интерполировать, более простую функцию. Разумеется, использование упрощенной функции не позволяет получить такие же точные результаты, какие давала бы первоначальная функция. Но в некоторых классах задач достигнутый выигрыш в простоте и скорости вычислений может перевесить получаемую погрешность в результатах.
Следует также упомянуть и совершенно другую разновидность математической интерполяции, известную под названием «интерполяция операторов». К классическим работам по интерполяции операторов относятся теорема Рисса — Торина и теорема Марцинкевича (Marcinkiewicz theorem), являющиеся основой для множества других работ.
Аппроксимация — замена одних математических объектов другими, имеющие похожие и близкие свойства для последующего использования в
прикладной задаче. Аппроксимация позволяет исследовать различные числовые характеристики или качественные свойства объекта изучения. Таким образом мы
можем свести задачу к исследованию более элементарных или удобных для вычислений объектов, характеристики которых известны или легко вычисляются.
Приближение имеет схожий смысл что и аппроксимация, термин «приближение» иногда употребляется в смысле приближающего объекта. Приближение функций
— нахождение для данной функции f функции g из некоторого определенного класса (например, среди полиномов заданной степени), в том или ином смысле близкой к f , дающей ее приближенное представление» .
Модель — любой образ какого-либо объекта, процесса или явления, используемый в качестве его аналога. Математическая модель — приближенное
описание какого-либо класса явлений из внешнего мира, выраженное с помощью математической символики и математического языка. Физическая модель —
приближенное описание некоторого объекта или явления с помощью образа, имеющего ту же физическую природу .
Один из самых важных этапов в изучении какого-либо объекта на основе математической модели данного объекта – удовлетворяет ли наша модель
нескольким критериям: соответствие изучаемому явлению и процессу, согласование результаты наблюдений и экспериментов с теоретическими
прогноза работы модели с учетом погрешности наблюдений. Поэтому необходима проверка модели на адекватность, то есть соответствие свойствам
реального объекта, при условии, что точность модели, должна быть больше точности наблюдений (ошибка модели должна быть меньше ошибки наблюдений).
Адекватность — соответствие, верность, точность. Точность измерения —
характеристика измерения, отражающая степень близости его результатов к
истинному значению измеряемой величины» .
Аппроксимация бывает двух видов:
Математическая аппроксимация в свою очередь подразделяется на несколько методов:
«Менее строгая аппроксимация — физическая или техническая аппроксимация, или математическая модель физического явления, процесса и его
физической модели, технического устройства и его характеристик, сигнала и его параметров, среды, материи и т.п. Физическая (техническая) аппроксимация
включает в себя множество способов приближения функций, которые выбирают, руководствуясь конкретно поставленной задачей. В итоге, с помощью физической
(технической) аппроксимации легко решается широкий спектр задач, актуальных на данный момент времени, связанных с конкретными проблемами и вопросами
прикладного (технического) характера. Строгая теория математической аппроксимации строится как фундаментальная, глобальная теория
аппроксимации, которая для решения текущих прикладных практических задач может и не пригодиться. Это может произойти вследствие либо потери с течением
времени актуальности решаемой задачи, либо сложности теории (аппроксимирующей функции), либо большого количества коэффициентов
аппроксимации» .
В основном, характеристические данные большинства сложных реальных процессов и явлений получают в результате опыта или эксперимента, очень редко
удается получить или вывести зависимость в виде аналитической. Для изучения явлений и процессов нужно для начала представить характеристики в формальной
математической форме, в которой их можно использовать для вычислений и расчетов . Простым и наглядным способом будет представление характеристик
в виде таблицы. Этот способ удобен для анализа при помощи ЭВМ, аргументы и функции образуют массивы данных. В ряде случаев характеристики реальных
процессов и явлений имеют сложный вид и нагляднее представить их в виде графиков, диаграмм или других графических изображений.
Применение экспериментальных данных в виде таблиц или графиков иногда оказывается не слишком удобным, и данные описывают при помощи
элементарных аналитических зависимостей, которые с достаточной точностью качественно отражают характер рассматриваемых соотношений [10]. В данном
случае возникает потребность в нахождении функции, наиболее близкой к исследуемой, таким образом мы сформулируем задачу аппроксимации.
Необходимо построить функцию по экспериментальным данным, приближенными аналитическими выражениями.
Для решения поставленной задачи необходимо получить аналитическую зависимость, то есть подобрать аппроксимирующую функцию, которая бы
удовлетворяла условиям достаточной простоты и отражала бы ключевые особенности экспериментально полученной функции с заранее заданной
степенью точности.
«Общая задача аппроксимации включает в себя две самостоятельные задачи:
Чтобы выбрать класс аппроксимирующей функции, необходимо решить
задачу, которая бы соблюдала некоторые требования:
Исходя из этого, функцию, которая будет приближать характеристику какоголибо объекта, выбирают руководствуясь физическими представлениями о
природе изучаемого явления или процесса. Выбор проходит, основываясь на внешнем сходстве исследуемой характеристики с графическим изображением
выбранной функции . К функции, которая является решением поставленной задачи предъявляются уже известные требования: обеспечивая хорошее качество
приближения с низкой среднеквадратической ошибкой, она должна быть простой и удобной для дальнейшего использования при решении на ЭВМ [10].
Аналитические выражения, отображающие характеристики реальных процессов должны как можно лучше соответствовать реальности. Однако
повышение точности аппроксимации приводит, как правило, к усложнению аппроксимирующих выражений и увеличению их количества, что затрудняет
определение и вычисление коэффициентов и применение этих выражений для анализа процессов .
Способов решения данной задачи существует большое количество, как и аналитических выражений, для которых необходимо найти значения
коэффициентов. Может быть нецелесообразно и не иметь смысла, стараться получить аппроксимирующие выражения, дающие наибольшую точность, чем
точность отдельных методов или конкретных характеристик процесса .
При решении задачи аппроксимации так же, как и при решении любой задачи, человек сталкивается с проблемой построения математической модели и поиска
компромисса в соотношении с точностью результатов и сложностью вычислений и самой модели .
«Определение коэффициентов аппроксимации наиболее плотно связано с запрашиваемой точностью. Точность определяется критериями приближения,
обычно применяют критерии равномерного, среднеквадратичного и интерполяционного или точечного приближений» . Если число заданных
точек превышает число определяемых коэффициентов аппроксимации, то лучшим путем будет использовать
метод наименьших квадратов , при котором
среднеквадратичная ошибка минимальна, так как прямое решение данной системы может не дать ответа. «Метод наименьших квадратов применяется, когда
необходима регулируемая и достаточно высокая точность аппроксимации. Для данного метода требуются громоздкие вычисления, что заставляет решать данную
задачу только при использовании компьютера, но имеется конструктивный подход для аналитического определения коэффициентов модели аппроксимации.
Метод наименьших квадратов обеспечивает наименьшую среднюю квадратическую ошибку аппроксимирующей функции от значений исходной
функции на заданном множестве точек, большим, чем число неизвестных коэффициентов» .
Необходимо отметить, что точность аналитического представления изучаемого явления будет тем выше, чем точнее выбранная нами математическая
модель, описывающая данное явление. Определимся с требованиями, которые нужно предъявить к выбору модели, описывающей явление или процесс при
одинаковой ее точности — наименьшее количество коэффициентов модели и ее простота, выполнение данных требований способствует уменьшению
систематической ошибки и времени обработки экспериментальных данных.
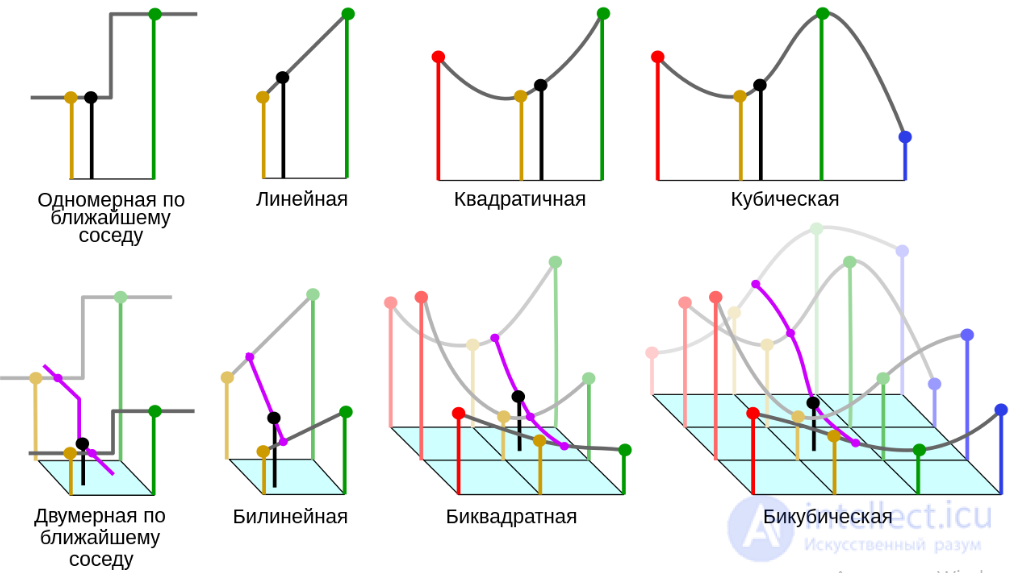
На интервале [a, b] заданы точки xi, i=0, 1,..., N; a ≤ x i ≤ b, и значения неизвестной функции в этих точках fi, i=0, 1,...., N. Требуется найти функцию F(x), принимающую в точках xi те же значения fi. Точки 
называются узлами интерполяции, а условия F(xi)= fi. – условиями интерполяции. При этом F(x) ищем только на отрезке [a,b]. Если необходимо найти функцию вне отрезка, то - это задачаэкстраполяции. Пока мы будем рассматривать только интерполяционные задачи.
Задача имеет много решений, т.к. через заданные точки (xi, fi), i=0, 1,..., N, можно провести бесконечно много кривых, каждая из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай аппроксимации функции многочленами, т.е. 
.
Все методы интерполяции можно разделить на локальные и глобальные. В случае локальной интерполяции на каждом интервале [xi–1, xi] строится отдельный полином. В случае глобальной интерполяции отыскивается единый полином на всем интервале [a, b]. При этом искомый полином называется интерполяционным полиномом.
Например, если наблюдения за ходом исследуемого бизнес-процесса (скажем, продаж) регистрировались в последний день каждой декады, то при необходимости оценить значения внутри данного интервала потребуется выполнить интерполяцию.
Точки x1,x2,…xn называются узлами интерполяции, их совокупность — интерполяционной сеткой, а расстояние между ее соседними узлами — шагом интерполяции, который может быть как равномерным, так и неравномерным. Об этом говорит сайт https://intellect.icu . Задача заключается в поиске интерполирующей функции F(xi)=yi. Иными словами, интерполяция позволяет узнать, какие значения принимает функция в точках, не являющихся ее узлами.
В настоящее время существует множество различных методов интерполяции. Выбор наиболее подходящего из них определяется требованием к точности, вычислительной сложности, гладкости интерполирующей функции, количеству точек данных и т.д.
Наиболее простым методом является линейная интерполяция, когда предполагается, что промежуточные точки лежат на прямых, соединяющих ее узлы (как показано на рисунке). Интерполирующая функция в этом случае имеет вид:
Очевидно, что если наблюдения фиксировались редко и шаг интерполяции большой, то данный метод может оказаться слишком грубым. Поэтому более часто используют интерполяцию полиномами (формула Ньютона, полиномы Лагранжа), сплайн-функциями и т.д.
Термин «интерполяция» впервые ввел английский математик Джон Валлис в 1656 году.
В технологиях анализа данных интерполяция используется для восстановления пропущенных значений, а также замены аномальных.
Если исходная функция f(x) задана аналитическим выражением, то при построении аппроксимирующей функции φ(x) возможно требовать минимальности отклонения одной функции от другой на некотором непрерывном множестве точек, например, на отрезке [a,b]. Такой вид аппроксимации называется непрерывным или интегральным.
Теоретически для наилучшего приближения целесообразно требовать, чтобы во всех точках некоторого отрезка [a,b] отклонения аппроксимирующей функции φ(x) от функции f(x) было по абсолютной величине меньше заданной величины ε>0 :
|f(x)-φ(x) | <ε, a<=x<=b
В этом случае говорят, что функция φ(x) равномерно приближает функцию f(x) с точностью ε на интервале [a,b] . Практическое получение равномерного приближения представляет большие трудности, и поэтому этот способ применяется главным образом в теоретических исследованиях.
Наиболее употребительным является так называемое среднеквадратичное приближение, для которого наименьшее значение имеет величина
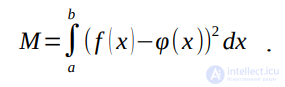
Потребовав обращения в нуль частных производных от М по параметрам, определяющим функцию φ(x) , получают уравнения, позволяющие найти наилучшие значения этих параметров.
Аппроксимация, при которой приближение строится на заданном дискретном множестве точек [xi] , называется точечной.
Для получения точечного среднеквадратичного приближения функции y=f(x), заданной таблично, аппроксимирующую функцию φ(x) строят из условия минимума величины
где yi – значения функции f(x) в точках xi.
Основная сфера применения среднеквадратичного приближения – обработка экспериментальных данных (построение эмпирических формул).
Другим видом точечной аппроксимации является интерполирование, при котором аппроксимирующая функция принимает в заданных точках xi, те же значения yi , что и функция f(x), т.е. φ(xi)=yi 
.
Рисунок 1 Среднеквадратическое приближение
В этом случае, близость интерполирующей функции к заданной функции состоит в том, что их значения совпадают на заданной системе точек.
На рис. 1 показаны качественные графики интерполяционной функции (сплошная линия) и результаты среднеквадратичного приближения (пунктирная линия). Точками отмечены табличные значения функции f(x).
Лагранж предложил строить интерполяционный полином в виде разложения
,
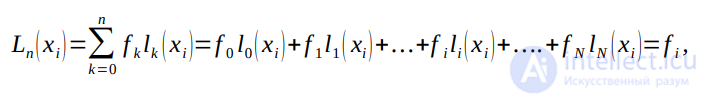где li(x) – базисные функции.
Для того, чтобы полином удовлетворял условиям Лагранжа, т.е. был бы интерполяционным, базисные функции li(x) должны обладать следующими свойствами:
1) быть полином степени n
2) удовлетворять условию
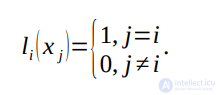
Лагранж показал, что функции, обладающие указанными свойствами, должны иметь следующий вид
.
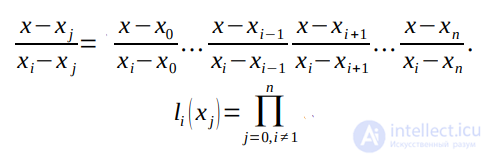С учетом этого выражения интерполяционный полином Лагранжа может быть записан в виде
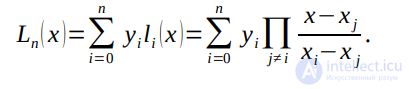
В отличие от интерполяционного полинома в канонической форме для вычисления значений полинома Лагранжа не требуется предварительно определять коэффициенты полинома путем решения системы уравнений. Однако для каждого значения аргумента x полином Лагранжа приходится пересчитывать вновь, коэффициенты же канонического полинома вычисляются только один раз. Поэтому практическое применение полинома Лагранжа оправдано только в том случае, когда интерполяционная функция вычисляется в сравнительно небольшом количестве точек x.
Интерполяционный полином Лагранжа оказывается очень удобным для приближенного вычисления определенных интегралов. Если, например, некоторую функцию заменить интерполяционным полином Лагранжа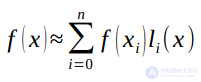 
, то определенный интеграл от нее может быть вычислен следующим образом
.
Значения интегралов от li(x) не зависят от f(x) и могут быть легко вычислены аналитически.
Рассмотрим еще одну форму записи интерполяционного полинома
Требования совпадения значений полинома с заданными значения функции в узловых точках Ni(xi)=yi, i=0,1,…,n приводит к системе линейных уравнений с треугольной матрицей для неизвестных коэффициентов 
:
,
решить которую не составляет труда.
Интерполяционный полином называется полиномом Ньютона. Интересная особенность полинома Ньютона состоит в том, что каждая частичная сумма его первых (m+1) слагаемых представляет собой интерполяционный полином степени m, построенный по первым (m+1) табличным данным.
Ошибка приближения функции f(x) интерполяционным полиномом n-й степени Ln(x) в точке x определяется разностью
.
Можно показать, что погрешность Rn(x) определяется следующим выражением
.
Здесь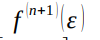 
– производная (n+1) порядка функции f(x) в некоторой точке 
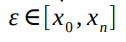, а функция ωn(x) определена как
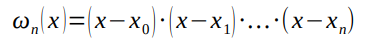
Если максимальное значение производной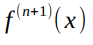
равно
,
то для погрешности интерполяции следует оценка
.
Конкретная величина погрешности в точке x зависит, очевидно, от значения функции ωn(x) в этой точке. Качественный характер зависимости ωn(x) показан на рис. 2.
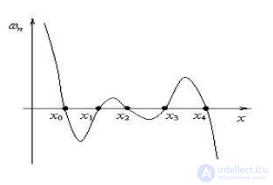
Рисунок 2 Погрешность интерполяции
Вследствие описанного поведения погрешности, глобальная интерполяция в некоторых случаях может давать совершенно неудовлетворительный результат. Из рисунка видно, что погрешность интерполяции тем выше, чем ближе точка x лежит к концам отрезка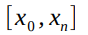 
. За пределами отрезка интерполяции (т.е. при экстраполяции) 
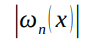быстро растет, поэтому погрешность возрастает существенно.
Пусть для исходных данных xi, fi, i=1,…,N (нумерацию лучше начинать с единицы), выбран вид эмпирической зависимости: y=φ(a0,a1,…,am) с неизвестными коэффициентами a0,a1,…,am . Запишем сумму квадратов отклонений между вычисленными по эмпирической формуле и заданными опытными данными:
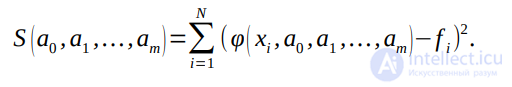
Параметры a0,a1,…,am будем находить из условия минимума функции S(a0,a1,…,am). В этом состоит метод наименьших квадратов (МНК).
Известно, что в точке минимума все частные производные от S по 
равны нулю:
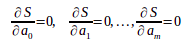
Рассмотрим применение МНК для частного случая, широко используемого на практике. В качестве эмпирической функции рассмотрим полином
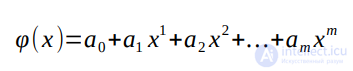
Формула (1) для определения суммы квадратов отклонений примет вид:
Вычислим производные
Приравнивая эти выражения к нулю и собирая коэффициенты при неизвестных a0,a1,…,am , получим следующую систему линейных уравнений
Данная система уравнений называется нормальной. Решая эту систему линейных уравнений, получаем коэффициенты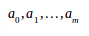 
.
В случае полинома первого порядка m=1, т.е. 
, система нормальных уравнений примет вид
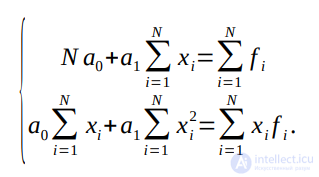
При m=2 имеем:
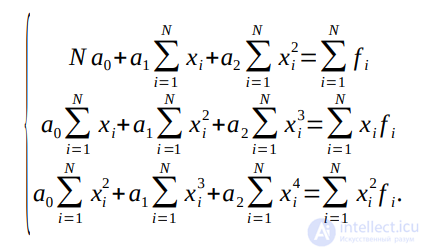
Как правило, выбирают несколько эмпирических зависимостей. По МНК находят коэффициенты этих зависимостей и среди них находят наилучшую по минимальной сумме отклонений.
При интерполировании функций мы использовали условие равенства значений интерполяционного полинома и данной функции в узлах интерполяции. Если же исходные данные получены в результате опытных измерений, то требование точного совпадения не нужно, так как данные не получены точно. В этих случаях можно требовать лишь приближенного выполнения условий интерполяции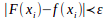 
. Это условие означает, что интерполирующая функция F(x) проходит не точно через заданные точки, а в некоторой их окрестности, так, например, как это показано на рис.
аппроксимация полином интерполяция формула
Рисунок 3
Тогда говорят о подборе эмпирических формул. Построение эмпирической формулы состоит из двух этапов подбора вида этой формулы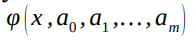 
, содержащей неизвестные параметры a0,a1,…,am, и определение наилучших в некотором смысле этих параметров. Вид формулы иногда известен из физических соображений (для упругой среды связь между напряжением и деформацией) или выбираются из геометрических соображений: экспериментальные точки наносятся на график и примерно угадывается общий вид зависимости путем сравнения полученной кривой с графиками известных функций. Успех здесь в значительной степени определяется опытом и интуицией исследователя.
Для практики важен случай аппроксимации функции многочленами, т.е. F(x)=a0+a1x+a2x2+…+amxm .
После того, как выбран вид эмпирической зависимости степень близости к эмпирическим данным определяется, используя минимум суммы квадратов отклонений вычисленных и экспериментальных данных.
На каждом отрезке [xi-1,xi] интерполяционный многочлен равен константе, а именно левому или правому значению функции.
Для левой кусочно-линейной интерполяции
F(x)= fi-1, если xi-1 ≤x
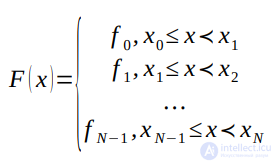
Для правой кусочно-линейной интерполяции F(x)= fi-1, если xi-1
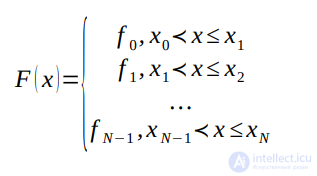
Легко понять, что условия интерполяция выполняются. Построенная функция является разрывной, что ограничивает ее применение. Для левой кусочно-линейной интерполяции имеем графическое представление
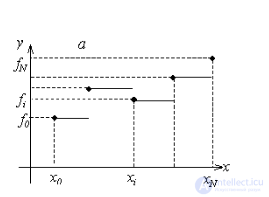
Рисунок 4 Кусочно-постоянная интерполяция
На каждом интервале [xi–1, xi] функция является линейной Fi(x)=kix+li. Значения коэффициентов находятся из выполнения условий интерполяции в концах отрезка:
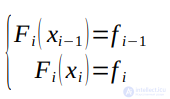
Получаем систему уравнений:
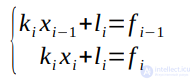
откуда находим
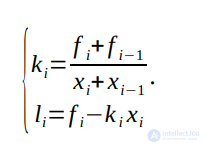
Следовательно, функцию F(x) можно записать в виде:
F(x)=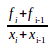 
x+ fi- kixi , если xi-1 <= x <=xi , т.е.
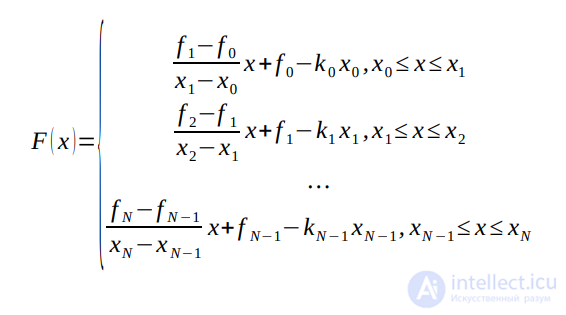
Или F(x)=ki ·(x-xi-1)+fi-1, ki = (fi - fi-1) / (xi - xi-1), xi-1 ≤ x ≤ xi, i=1,2,...,N-1
При использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение x, а затем подставить его в формулу.
Итоговая функция будет непрерывной, но производная будет разрывной в каждом узле интерполяции. Погрешность такой интерполяции будет меньше, чем в случае кусочно–постоянной интерполяции. Иллюстрация кусочно–линейной интерполяции приведена на рисунке
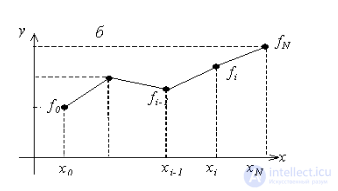
Рисунок 5 Кусочно-линейная интерполяция
На каждом отрезке 
интерполяционный многочлен равен константе, а именно левому или правому значению функции.
Для левой кусочно-линейной интерполяции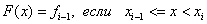 
, т.е.
Для правой кусочно-линейной интерполяции 
, т.е.
Легко понять, что условия интерполяция выполняются. Построенная функция является разрывной), что ограничивает ее применение. Для левой кусочно-линейной интерполяции имеем графическое представление:
На каждом интервале [xi–1, xi] функция является линейной 
. Значения коэффициентов находятся из выполнения условий интерполяции в концах отрезка: 
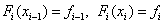. Получаем систему уравнений: 
, откуда находим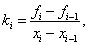 
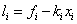. Следовательно, функцию F(z) можно записать в виде:
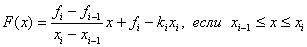, т.е.
Или F(x) = ki * (x - xi-1) + fi-1,
ki = (fi - fi-1) / (xi - xi-1), xi-1 ≤ x ≤ xi, i=1,2,...,N-1
При использовании линейной интерполяции сначала нужно определить интервал, в который попадает значение x, а затем подставить его в формулу.
Итоговая функция будет непрерывной, но производная будет разрывной в каждом узле интерполяции. Погрешность такой интерполяции будет меньше, чем в случае кусочно–постоянной интерполяции. Иллюстрация кусочно–линейной интерполяции приведена на рисунке
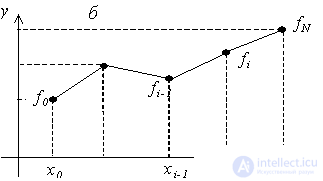
Пример: Заданы значений некоторой функции:
| x | 0 | 2 | 3 | 3.5 |
| f | -1 | 0.2 | 0.5 | 0.8 |
Требуется найти значение функции при z=1 и z=3.2 по кусочно–постоянной и кусочно–линейной интерполяции.
Решение. Точка z=1 принадлежит первому локальному отрезку [0, 2], т.е.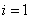 
и, следовательно, по формулам левой кусочно–постоянной интерполяции F(1) = f0 = –1, по формулам правой кусочно–постоянной интерполяции F(1)=f1=0.2. Воспользуемся формулами кусочно–линейной интерполяции:
.
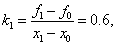
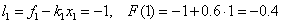Точка z=3.2 принадлежит третьему интервалу [3, 3.5], т.е.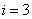 
и, следовательно, по формулам левой кусочно – постоянной интерполяции F(3.2)=
=0.5, по формулам правой кусочно – постоянной интерполяции F(3.2)= 
=0.8. Воспользуемся формулами кусочно–линейной интерполяции:
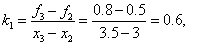
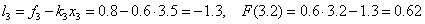
Слово сплайн (английское слово "spline") означает гибкую линейку, используемую для проведения гладких кривых через заданные точки на плоскости. Форма этого универсального лекала на каждом отрезке описывается кубической параболой. Сплайны широко используются в инженерных приложениях, в частности, в компьютерной графике. Итак, на каждом i–м отрезке [xi–1, xi], i=1, 2,…, N, решение будем искать в виде полинома третьей степени:
Si(x)=ai+bi(x–xi)+ci(x–xi)2/2+di(x–xi)3/6
Неизвестные коэффициенты ai, bi, ci, di, i=1, 2,..., N, находим из:
• условий интерполяции: Si(xi)=fi, i=1, 2,..., N; S1(x0)=f0,
• непрерывности функции Si(xi–1)=Si–1(xi–1), i=2, 3,..., N,
• непрерывности первой и второй производной:
S /i(xi–1)=S /i–1(xi–1), S //i(xi–1)=S //i–1(x i–1), i=2, 3,..., N.
Учитывая, что 
, для определения 4N неизвестных получаем систему 4N–2 уравнений:
ai=fi, i=1, 2,..., N,
bi hi – cihi2/2 + di hi3/6=fi – fi–1, i=1, 2,..., N,
bi – bi–1 = ci hi – di hi2/2, i=2, 3,..., N,
di hi = ci – ci–1 , i=2, 3,..., N.
где hi=xi – xi–1. Недостающие два уравнения выводятся из дополнительных условий: S //(a)=S //(b)=0. Можно показать, что при этом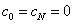 
. Из системы можно исключить неизвестные bi , di , получив систему N+1 линейных уравнений (СЛАУ) для определения коэффициентов ci:
c0 =0, cN =0,
hici–1+2(hi+hi+1)ci+h i+1ci+1=6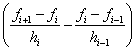
, i=1, 2,…, N–1. (1)
После этого вычисляются коэффициенты bi, di:
, i=1, 2,..., N. (2)
В случае постоянной сетки hi=h эта система уравнений упрощается.
Данная CЛАУ имеет трехдиагональную матрицу и решается методом прогонки.
Коэффициенты 
определяются из формул:
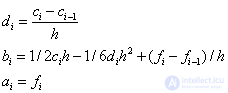
Для вычисления значения S(x) в произвольной точке отрезка z∈[a, b] необходимо решить систему уравнений на коэффициенты ci, i=1,2,…, N–1, затем найти все коэффициенты bi, di. Далее, необходимо определить, на какой интервал [xi0, xi0–1] попадает эта точка, и, зная номер i0, вычислить значение сплайна и его производных в точке z
S(z)=ai0 +bi0(z–xi0)+ci0(z–xi0)2/2+di0(z–x i0)3/6
S /(z)=bi0+ci0(z–xi0)+di0(z–x i0)2/2, S //(z)=ci0+di0(z–x i0).
Пример.
|
|
x0,f0 |
x1,f1 |
x2,f2 |
x3,f3 |
x4,f4 |
|
х |
0 |
¼ |
1/2 |
3/4 |
1 |
|
f |
1 |
2 |
1 |
0 |
1 |
Требуется вычислить значения функции в точках 0.25 и 0.8, используя сплайн – интерполяцию.
В нашем случае: hi=1/4,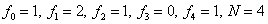 
.
Выпишем систему уравнений для определения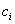 
:
Решая эту систему линейных уравнений, получим: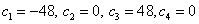 
.
Рассмотрим точку 0.25, которая принадлежит первому отрезку, т.е. 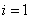. Следовательно, получим,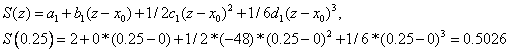 
Рассмотрим точку 0.8, которая принадлежит четвертому отрезку, т.е.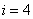 
.
Следовательно, 
В случае глобальной интерполяции отыскивается единый полином на всем интервале [a, b], т.е. строится полином, который используется для интерполяции функции f(x) на всем интервале изменения аргумента x. Будем искать интерполирующую функцию в виде полинома (многочлена) m–ой степени Pm(x)=a0+a1x+a2x2+a3x3+…+am xm. Какова должна быть степень многочлена, чтобы удовлетворить всем условиям интерполяции? Допустим, что заданы две точки: (x0, f0) и (x1, f1), т.е. N=1. Через эти точки можно провести единственную прямую, т.е. интерполирующей функцией будет полином первой степениP1(x)=a0+a1x. Через три точки (N=2) можно провести параболу P2(x)=a0+a1x+a2x2 и т.д. Рассуждая таким способом, можно предположить, что искомый полином должен иметь степень N .
Для того, чтобы доказать это, выпишем систему уравнений на коэффициенты. Уравнения системы представляют собой условия интерполяции в при каждом x=xi:
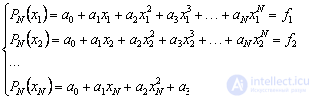
Данная система является линейной относительно искомых коэффициентов a0, a1, a2,…, aN. Известно, что СЛАУ имеет решение, если ее определитель отличен от нуля. Определитель данной системы
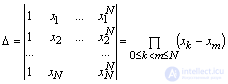
носит имя определителя Вандермонда. Из курса математического анализа известно, что он отличен от нуля, если xk≠ xm (т.е. все узлы интерполяции различные). Таким образом, доказано, что система имеет решение.
Мы показали, что для нахождения коэффициентов
a0, a1, a2,…, aN надо решить СЛАУ, что является сложной задачей. Но есть другой способ построения полинома N–й степени, который не требует решения такой системы.
Решение ищем в виде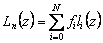 
, где li(z) – базисные полиномы N–й степени, для которых выполняется условие: 
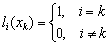. Убедимся в том, что если такие полиномы построены, то LN(x) будет удовлетворять условиям интерполяции:
.
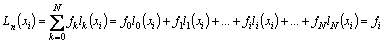Каким образом построить базисные полиномы? Определим
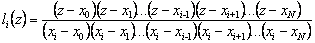, i=0, 1,..., N.
Легко понять, что
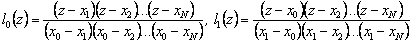, и т.д.
Функция li(z) является полиномом N–й степени от z и для нее выполняются условия "базисности":
=0, i≠k;, т.е. k=1,…,i-1 или k=i+1,…,N.
.
Таким образом, нам удалось решить задачу о построении интерполирующего полинома N– й степени, и для этого не нужно решать СЛАУ. Полином Лагранжа можно записать в виде компактной формулы: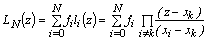 
. Погрешность этой формулы можно оценить, если исходная функция g(x) имеет производные до N+1 порядка:
.
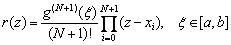Из этой формулы следует, что погрешность метода зависит от свойств функции g(x), а также от расположения узлов интерполяции и точки z. Как показывают расчетные эксперименты, полином Лагранжа имеет малую погрешность при небольших значениях N<20. При бόльших N погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (т.е. его погрешность не убывает с ростом N).
Рассмотрим частные случаи. Пусть N=1, т.е. заданы значения функции только в двух точках. Тогда базовые полиномы имеют вид:
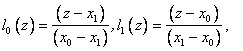
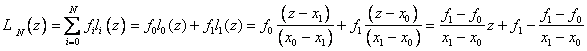, т.е. получаем формулы кусочно–линейной интерполяции.
Пусть N=2. Тогда: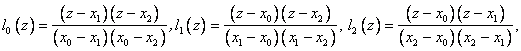 
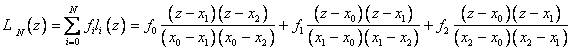
В результате мы получили формулы так называемой квадратичной или параболической интерполяции.
Пример: Заданы значений некоторой функции:
| x | 0 | 2 | 3 | 3.5 |
| f | -1 | 0.2 | 0.5 | 0.8 |
Требуется найти значение функции при z=1, используя интерполяционный полином Лгранжа. Для этого случая N=3, т.е. полином Лагранжа имеет третий порядок. Вычислим значения базисных полиномов приz=1:
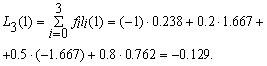
При интерполировании функций мы использовали условие равенства значений интерполяционного полинома и данной функции в узлах интерполяции. Если же исходные данные получены в результате опытных измерений, то требование точного совпадения не нужно, так как данные не получены точно. В этих случаях можно требовать лишь приближенного выполнения условий интерполяции 
. Это условие означает, что интерполирующая функция F(x) проходит не точно через заданные точки, а в некоторой их окрестности, так, например, как это показано на рис.
Тогда говорят о подборе эмпирических формул. Построение эмпирической формулы состоит из двух этапов6 подбора вида этой формулы 
, содержащей неизвестные параметры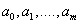 
, и определение наилучших в некотором смысле этих параметров. Вид формулы иногда известен из физических соображений (для упругой среды связь между напряжением и деформацией) или выбираются из геометрических соображений: экспериментальные точки наносятся на график и примерно угадывается общий вид зависимости путем сравнения полученной кривой с графиками извесиных функций. Успех здесь в значительной степени определяется опытом и интуицией исследователя.
Для практики важен случай аппроксимации функции многочленами, т.е. .
После того, как выбран вид эмпирической зависимости степень близости к эмпирическим данным определяется, используя минимум суммы квадратов отклонений вычисленных и экспериментальных данных.
Пусть для исходных данных xi, fi, i=1,…,N (нумерацию лучше начинать с единицы), выбран вид эмпирической зависимости: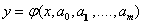 
с неизвестными коэффициентами 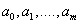. Запишем сумму квадратов отклонений между вычисленными по эмпирической формуле и заданными опытными данными:
.
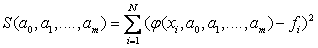Параметры 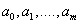будем находить из условия минимума функции 
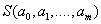. В этом состоит метод наименьших квадратов (МНК).
Известно, что в точке минимума все частные производные от 
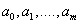по равны нулю:
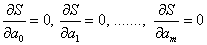(1)
Рассмотрим применение МНК для частного случая, широко используемого на практике. В качестве эмпирической функции рассмотрим полином
.
Формула (1) для определения суммы квадратов отклонений примет вид:
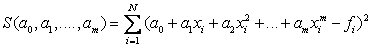(2)
Вычислим производные:
Приравнивая эти выражения нулю и собирая коэффициенты при неизвестных 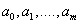, получим следующую систему линейных уравнений:
Данная система уравнений называется нормальной. Решая эту систему линейных уравнений, получаем коэффициенты .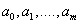
В случае полинома первого порядка m=1, т.е.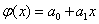 
, система нормальных уравнений примет вид:
При m=2 имеем:
Как правило, выбирают несколько эмпирических зависимостей. По МНК находят коэффициенты этих зависимостей и среди них находят наилучшую по минимальной сумме отклонений.
Пример. Заданы координаты точек:
|
x |
-5 |
-3.5 |
-2 |
1.5 |
3.25 |
5 |
|
f |
0.5 |
1.2 |
1.4 |
1.6 |
1.7 |
1.5 |
т.е. N=6. Требуется найти эмпирические зависимости: линейную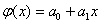 
, квадратичную 
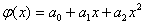, гиперболическую 
по методу МНК и выбрать среди них наилучшую по наименьшей сумме квадратов отклонений.
Система нормальных уравнений для линейной зависимости:
Учитывая, что N=6,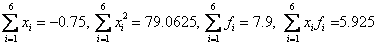 
, получим
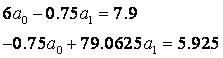
Решая систему линейных уравнений, получим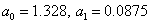 
. Следовательно, линейная зависимость имеет вид: 
.
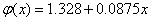Вычислим сумму квадратов отклонений: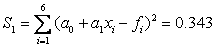 
.
Рассмотрим квадратичную зависимость. Система нормальных уравнений имеет вид
Найдем неподсчитанные суммы: 
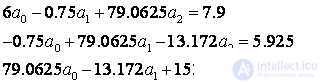
Решая СЛАУ, получим 
Следовательно, квадратичная зависимость имеет вид: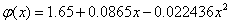 
.
Вычислим сумму квадратов отклонений: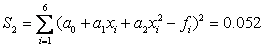 
.
Выпишем систему нормальных уравнений для гиперболической зависимости. Согласно МНК находим сумму квадратов отклонений:
. Составляем систему нормальных уравнений:
Или
Учитывая, что 
, получим
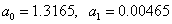
Сумма квадратов отклонений: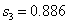
Из трех зависимостей выбираем наилучшую, т.е. квадратичную.
Я хотел бы услышать твое мнение про аппроксимация функций Надеюсь, что теперь ты понял что такое аппроксимация функций, интерполяция , интерполяция функций, аппроксимация, интерполирование, непрерывная аппроксимация, точечная аппроксимация, интерполяционный полином лагранжа, интерполяционный полином ньютона, погрешность глобальной интерполяции, метод наименьших квадратов, подбор эмпирических формул, кусочно-постоянная интерполяция, кусочно-линейная интерполяция и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Численные методы
Комментарии
Оставить комментарий
Численные методы
Термины: Численные методы