1.1.Основные понятия теории идентификации

теория идентификации — это раздел прикладной математики и системного анализа, который занимается вопросами построения математических моделей динамических систем на основе данных о поведении этих систем. Основная цель идентификации — создание моделей, которые могут точно описывать поведение системы, даже если ее внутренняя структура частично или полностью неизвестна.

Ключевые аспекты теории идентификации включают:

1. Моделирование системы: Создание математической модели, которая описывает динамику системы. Модели могут быть линейными или нелинейными, детерминированными или стохастическими.

2. Сбор данных: Для идентификации системы необходимы данные о входных и выходных сигналах системы (напр., данные о реакции системы на внешние воздействия).

3. Оценка параметров: Основная задача — найти параметры модели, такие как коэффициенты, которые лучше всего описывают систему. Методы оптимизации используются для минимизации разницы между наблюдаемыми данными и результатами модели.

4. Методы идентификации:

   • Методы на основе наблюдений (например, метод наименьших квадратов, метод максимального правдоподобия).
   • Методы адаптивного управления для систем, параметры которых меняются со временем.
   • Нейросетевые методы и машинное обучение, которые помогают в случаях, когда структура системы сложна и данные включают сильный шум.

5. Идентифицируемость: Это свойство системы, которое говорит о том, возможно ли однозначно определить параметры модели на основе имеющихся данных.

6. Валидация моделей: После идентификации проводится проверка на то, насколько хорошо модель соответствует реальному поведению системы, используя тестовые данные или другие подходы, такие как кросс-валидация.

Примеры применения теории идентификации включают автоматическое управление, диагностику и прогнозирование технических систем, биологические системы, финансовые модели и другие сложные динамические процессы.

Внастоящее время проблемы, связанные с созданием математических моделей объектов технологических процессов, экономики и живой природы, формируют одно из основных направлений науки и техники – моделирование. Это объясняется тем, что математические модели объектов широко применяются как при создании систем управления этими объектами, так и при их эксплуатации.

В данном учебном пособии рассматриваются только модели технических объектов и систем. Объекты и системы представляют собой совокупность материальных тел, находящихся в непрерывном взаимодействии друг c другом и с окружающей средой. Построение математической модели объекта может производиться несколькими методами: аналитическим, экспериментальным и экспериментально-аналитическим [1–3].

Аналитический метод предусматривает получение математического описания объекта на основе законов физики, механики, химии и т.д. Такой подход дает положительный результат, если рассматриваемый объект достаточно прост по структуре и хорошо изучен. Если же объект изучен недостаточно или же настолько сложен, что аналитическое описание его математической моделью практически невозможно, прибегают к экспериментальным методам, суть которых сводится к статистической обработке технологических данных. При экс- периментально-аналитическом методе априорная модель, полученная аналитическим путем, уточняется в соответствующих экспериментах.

Взаимодействие объекта с окружающей средой можно представить в виде рисунка (рис. 1.1).

Совокупность таких воздействий окружающего мира на объект можно разделить на две группы в соответствии с характером влияния среды на переменные состояния объекта. В первую группу входят те воздействия, которые в точке приложения изменяют переменные состояния аддитивно. Это означает, что сигналы, пропорциональные этим воздействиям, суммируются с сигналами, пропорциональными соответствующим переменным состояния.

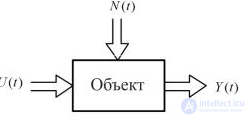
Рис. 1.1. Структурная схема объекта управления

Эти воздействия называют внешними. Среди внешних воздействий выделяют: U (t) – входные воздействия, N(t) – возмущающие воздействия.

Вторая группа воздействий внешней среды изменяет переменные состояния объекта косвенно, обычно неаддитивно. Эти воздействия приводят к изменению оператора объекта (системы) А, под которым понимают закон преобразования входных воздействий в выходные переменные объекта. Такие воздействия называются операторными.

Поведение объекта описывается вектором Y (t).

Схему взаимовоздействия с окружающей средой можно представить более подробно (рис. 1.2).

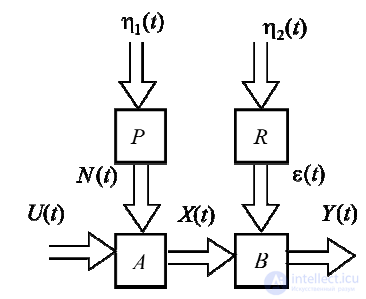
Рис. 1.2. Структурная схема модели объекта управления

На схеме приняты следующие обозначения:

• U (t), Y (t) – наблюдаемые входные и выходные сигналы. Они

могут быть детерминированными или случайными, могут быть смесью (обычно аддитивной) детерминированной и случайной составляющих. Входные сигналы могут специально подаваться в систему для идентификации (активный эксперимент), а могут существовать в системе как управляющие или возмущающие воздействия (пассивный эксперимент);

•X (t) – ненаблюдаемые сигналы, которые оцениваются косвенно по сигналу Y (t) , полученному в результате преобразования в объекте оператором B ;

•η1(t), η2 (t) – ненаблюдаемые помехи, являющиеся, как правило,

случайными процессами типа белого шума, в некоторых случаях содержащие детерминированные совпадающие;

• N(t), ε(t) – чаще ненаблюдаемые, обычно коррелированные во

времени случайные сигналы, в некоторых случаях содержащие детерминированные составляющие;

• A, B, P, R – операторы, в некоторых случаях их вид не известен, в других известен, но не известны параметры.

Согласно приведенной структурной схеме модели объекта (см. рис. 1.1) основными задачами идентификации являются следующие:

1. Задача нахождения характеристик (параметров) объекта.

По известным наблюдаемым переменным U (t), Y (t) требуется определить операторы (или параметры операторов) A, B. Часто одновременно с определением параметров A, B требуется установить параметры операторов P, R, преобразующих ненаблюдаемые белые шумы η1(t), η2 (t) в ненаблюдаемые сигналы N(t), ε(t).

2. Задача оценивания переменных состояния.

Состояние объекта характеризуется вектором переменных состояния X (t) , вектором, однозначно определяющим все его характеристики. По известным наблюдаемым сигналам U (t), Y (t) при известных операторах A, B, P, R с известными параметрами требуется определить (оценить) ненаблюдаемый сигнал X (t) . Иногда возникает задача совместного оценивания параметров и состояния.

3. Задача генерации случайных сигналов с заданными характеристиками или определения характеристик случайных сигналов.

По наблюдаемым переменным N(t), ε(t) требуется определить оператор (или параметры оператора) P, R.

Задача идентификации включает в себя следующие этапы :

•сформулировать требования к данным наблюдений: как выполнить сбор экспериментальных данных, как использовать эти данные, собранные в реальных условиях проведения эксперимента ;

•определить класс объектов – совокупность моделей-кандидатов, из которой впоследствии будет отобрана наилучшая модель;

•сформировать так называемую функцию потерь или риска (критерий оптимальности), характеризующую адекватность объекта и настраиваемой модели, и на ее основе сформулировать критерий качества идентификации;

•выбрать способ оценки степени соответствия исследуемой модели экспериментальным данным;

•определить процедуру верификации модели: провести проверку

иподтверждение адекватности модели, т.е. выяснить, в какой степени модель действительно «объясняет» поведение изучаемой системы.

При построении математических моделей существенную роль играют следующие факторы .

1. До начала эксперимента необходимо определить условия, в которых будет проводиться сбор данных, решить вопросы дальнейшего конкретного их использования. Эти задачи решаются на этапе планирования эксперимента путем выбора числа опытов эксперимента и условий его проведения, необходимых и достаточных для решения поставленной задачи с требуемой точностью. Этот этап непосредственно не относится

кидентификации, а предваряетее.

2. В конструктивном смысле идентификация – это определение по входным и выходным воздействиям такой модели из определенного класса моделей, которой реальная исследуемая система эквивалентна.

В соответствии с этим нужно определить класс моделей, среди которых будет выбрана наиболее подходящая. На этом этапе необходимо выбрать общую структуру модели и класс уравнений, которыми предполагается описывать наблюдаемый процесс. Этот этап иногда называется идентификацией в широком смысле (или структурной идентификацией) и зачастую оказывается решающим фактором. Для успешного решения задачи структурной идентификации требуется использовать априорные сведения о физических, химических или иных явлениях, происходящих в процессе, знание формальных аналитических свойств моделей, инженерные навыки и интуицию. До настоящего времени общих формальных подходов к решению задачи структурной идентификации не существует, и этап структурной идентификации часто сводится к эвристическому заданию структуры модели на основе априорных сведений об объекте.

3.Близость полученной модели реальной исследуемой системе достаточно относительна, так как операторы объекта и модели могут быть описаны на разных языках, иметь разную структуру или количество входов, и потому понятие адекватности может быть сформулировано разными способами. Поскольку непосредственно оценить близость операторов объекта и модели сложно или зачастую невозможно, наиболее часто оценивается близость выходных величин объекта и модели или математического ожидания ошибок оценок параметров. Для этого вводится понятие функции потерь или риска, в дальнейшем подлежащей минимизации. Далее для выбора «наилучшей» модели из определенного класса на основании этой функции потерь формируется некоторый критерий, и в дальнейшем задача идентификации становится задачей оптимизации выбранного критерия.

4.После определения структуры модели и класса уравнений необходимо установить численные значения параметров – коэффициенты дифференциальных, разностных, интегральных уравнений или других математических конструкций линейной или нелинейной модели объекта и (или) состояний, вошедших в уравнения математической модели. Таким образом, решению подлежит задача оценивания параметров и (или) состояний по имеющимся экспериментальным данным, т.е. по значениям измеряемых переменных. Данная задача называется задачей параметрической идентификации (или идентификацией в узком смысле). При оценивании параметров приходится решать задачу минимизации некоторых функциональных зависимостей от измеряемых величин (обычно от разности выходных сигналов модели и объекта) и от неизмеряемых величин – параметров и состояний. Для решения этой задачи необходимо разработать алгоритм идентификации, который на основе доступных для наблюдения входных и выходных величин определял бы параметры настраиваемой модели, минимизирующий погрешность модельного описания в соответствии с выбранным функционалом качества.

5.Переход от этапа построения модели к последующему ее использованию требует оценки качества полученной модели, т.е. проверки адекватности модели объекту. Вследствие того что абсолютная эквивалентность модели объекту принципиально недостижима, основным условием подтверждения адекватности полученной модели является возможность ее использования для решения той задачи, ради которой эта модель строилась. Поэтому адекватность предполагает воспроизведение моделью с необходимой полнотой всех свойств объекта, существенных для целей данного исследования. Степень адекватности модели и объекта обычно оценивают путем сравнения их выходных сигналов при подаче одинаковых входных воздействий на объект и его модель. Это сравнение предпочтительно производить на основе новой информации, отличной от данных, которые использовались в процессе идентификации объекта.

В большинстве реальных ситуаций взаимодействие объекта с окружающей средой соответствует следующей стандартной схеме (рис. 1.3):

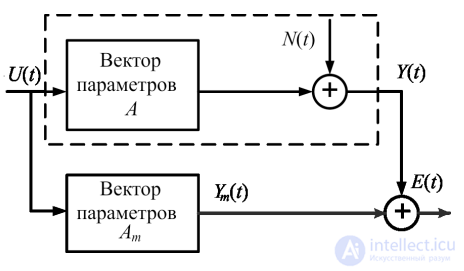
Рис. 1.3. Типовая схема наблюдений при идентификации объекта

На схеме приняты следующие обозначения: U (t) – вектор входных воздействий;

Y (t) – вектор выходных воздействий объекта; Ym (t) – вектор выходных воздействий модели;

N(t) – вектор неконтролируемых случайных воздействий;

E(t) – вектор разности (невязки) между выходами объекта и модели;

A – вектор параметров объекта; Am – вектор параметров модели.

Идентификационный эксперимент в соответствии со структурной схемой наблюдения состоит в следующем.

На входы объекта и модели подается внешнее воздействие. В реальных условиях взаимодействия объекта со средой сигналы наблюдения за объектом искажены случайными возмущениями, определяющимися спецификой функционирования самого объекта, погрешностями методов и средств измерений и неконтролируемыми воздействиями внешней среды. При использовании такой схемы наблюдений считается, что обобщенный вектор помех N(t) включает в себя все внешние возмущения, отклонения измеренных значений от истинных воздействий и другие факторы. Обычно в результате эксперимента получают наблюдения входа и выхода, т.е. реализации случайных функций U (t) и Y (t) .

Закон функционирования объекта может быть представлен в следующем виде:

Y (t) = F0 (U (t), N(t), A). (1.1)

В соответствии с зависимостью (1.1) выходная величина объекта зависит от внешнего воздействия U (t) u(t), помехи N(t) и от неизвестного вектора параметров A , значения которых непосредственному наблюдению недоступны.

На основании сведений об объекте формируется модель, под которой понимается некоторый оператор F , преобразующий наблюдаемое входное воздействие U (t) в ее реакцию Y (t) у, (t):

Ym (t) = F(U (t), Am ). (1.2)

Модель (1.2) описывается уравнениями, подобными уравнениям объекта (1.1) и содержащими информацию об измеряемых входных и выходных величинах, причем полагается, что помехи не меняют вида модели. Коэффициенты этих уравнений являются параметрами модели. Выходная величина модели зависит от параметров Am , которые

рассчитываются на основе алгоритма, обрабатывающего вектор всех наблюдений. Для нахождения вектора параметров Am необходимо определить оптимальный, в смысле подобия объекту, способ корректировки модели. При таком подходе задача идентификации заключается в построении модельного оператора F из некоторого класса операторов (задача структурной идентификации) и определении по наблюдениям U (t) и Y (t) вектора параметров Am (параметрическая идентификация), такого, чтобы выходной сигнал модели был бы наиболее близок к выходному сигналу объекта.

На основе сравнения искаженного помехой N(t) выходного сигнала объекта Y (t) = F0 (U (t), N(t), A) с выходным сигналом модели Ym (t) = F(U (t), Am ) рассчитывается невязка – разность выходных величин объекта и модели:

E(t) =Y (t) −Ym (t). (1.3)

Для оценки соответствия модели объекту вводится функция потерь (функция невязки) F(Y (t), Ym (t), A), зависящая от выходов объекта и модели, параметров модели.

На основе функции невязки формулируется критерий идентификации:

J (Y, Ym , A) = J{F(Y, Ym , A)}. (1.4)

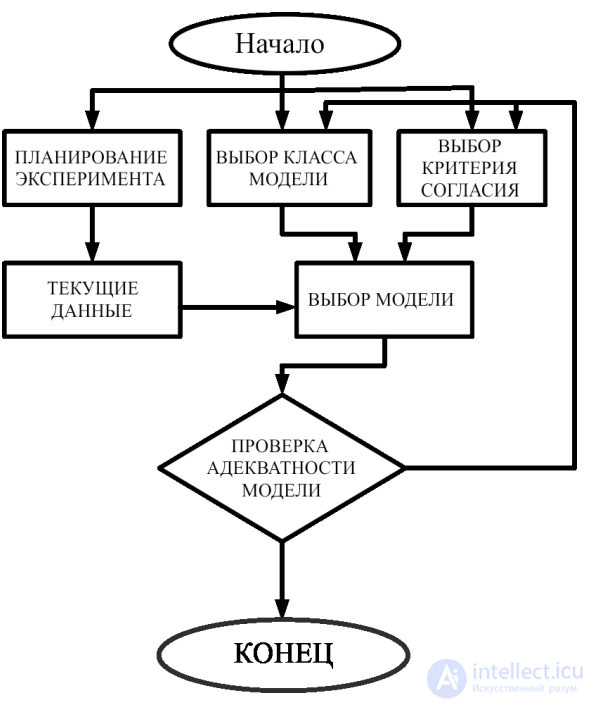
Рис. 1.4. Общая схема идентификации модели

Критерий качества идентификации, характеризующий адекватность модели реальному объекту, представляет собой средние потери. Чем меньше средние потери, тем выше качество идентификации.

Минимизация функционала идентификации, соответствующая улучшению качества идентификации, осуществляется путем надлежащего выбора структуры модели и изменением значений ее параметров. Процедура изменения реализуется алгоритмом идентификации.

Существуют разные способы оценивания параметров, различающиеся между собой по используемому критерию оптимальности и имеющейся априорной информации. В определенной степени выбор критерия оптимальности субъективен, а процедура оценивания существенно зависит от принятого критерия.

Общая схема идентификации представлена на рис. 1.4.

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.