Лекция
Сразу хочу сказать, что здесь никакой воды про теория приемных антенн, и только нужная информация. Для того чтобы лучше понимать что такое теория приемных антенн, Приемная антенна , настоятельно рекомендую прочитать все из категории Устройства СВЧ и антенны.
Приемная антенна преобразует энергию радиоволн в энергии токов высокой частоты.
Она является, таким образом, маломощным генератором переменного тока,
нагрузкой которогослужит входное сопротивление приемника.
При рассмотрении приемной антеннынас будут интересовать следующие вопросы:
Исследование приемной антенны можно производить двумя различными методами. Первый из них состоит в
непосредственном анализе воздействия приходящей волны на приемнуюантенну (рис. П.1.1).
В частности, в случае проволочной антенны поступают следующим образом. Антенну мысленно разбивают
на элементарные вибраторы и находят ЭДС, наводимую вкаждом элементарном вибраторе. Суммируя эти
ЭДС по всем элементам антенны, определяют ЭДС на клеммах ее. Зная ЭДС, можно определить ток на входе приемникаи другие параметры приемной антенны.
_img_367.jpg)
_img_368.jpg)

Рис. П.1.1 — Симметричныйвибратор в поле действия плоскойволны
Поле, создающее ЭДС на элементарном излучателе d z определяется соотношение 
Элементарная ЭДС 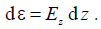 .
.
В общем случае для произвольной антенны этот метод оказывается весьма сложным. Поэтому, как правило, пользуются вторым методом, основанным на применении известного из теориипассивных линейных четырехполюсников принципа взаимности. Принцип взаимности позволяет определить свойства и параметры приемной антенны, если известны свойства и параметры этойже антенны при работе ее в качестве передающей. Справедливость принципа взаимности для антенн была доказана в 1927 г. М. П. Свешниковой. На основе этого принципа М. С. Нейманом в1935 г. была разработана теория приемных антенн .
Теорема взаимности. Рассмотрим две произвольные и произвольно ориентированные в пространстве антенны А1 и А2 (рис. П.1.2). Промежуточная среда считается линейной(характеристики ее не зависят от величины напряженности поля) и изотропной.

Рис. П.1.2 — Взаимное расположение передающейи приемной антенн Как было доказано М. П. Свешниковой,
систему из двух антенн можно рассматривать каклинейный пассивный четырехполюсник с зажимами 1—1 и 2—12.
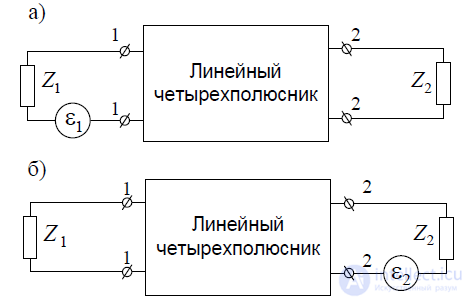
Рис. П.1.3 — Модели линейных четырехполюсников
Рассмотрим токи на входе и выходе такого четырехполюсника для двух случаев. Первый случай, когда А1 — передающая антенна; А2 — приемная (рис. П.1.3, а). На входе и выходевключены дополнительные сопротивления Z1 и Z2, которые можно рассматривать как внутреннее сопротивление источника ЭДС и сопротивление нагрузки (входное сопротивление приемника)соответственно. Пусть в этом случае при ЭДС 1 ток на выходе четырехполюсника (ток в нагрузке) будет I21. Второй случай, когда А2 — передающая антенна; А1 — приемная (рис. П.1.3, б).Величину ЭДС в этом случае положим равной 2 и ток на входныхзажимах приемнойантенныбудет составлять I112.

Это соотношение и будет использовано далее для нахождения амплитуд тока и ЭДС в приемной антенне.
Дальнейшее рассмотрение проводится для антенн с линейной поляризацией поля. Считаем известными параметры обеих антенн в режиме передачи 
Так как мы хотим найти ток в приемной антенне в зависимости от величины поля, падающего на антенну, то необходимо выразить ЭДС 1 и 2 через параметры антенны при работе их напередачу и поля, создаваемые этими антеннами. Полагаем, что антенны находятсявдальней зоне друготносительно друга. Расстояние между ними — r .
Амплитуда поля, возбуждаемого антенной А1 возле антенны А2


_img_377.jpg)
Соберем все, что относится к антенне А1, влево, а к антенне А2 — вправо, тогда получим
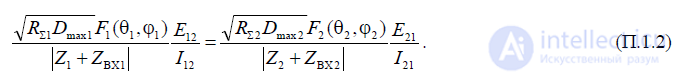
Левая часть выражения (П.1.2) зависит лишь от параметров первой антенны. Величина
E12 зависит, конечно, от параметров второй антенны, но отношение E12 к вызванному ею же току в первой антенне I12
зависит лишь от параметров первой антенны.
Таким образом, в (П.1.2)слева и справа стоят две независимые величины. Левая часть зависит от параметров первой антенны,
правая — от параметров второй антенны. Это дает основание заключить,
что каждая из этихвеличин порознь равна одной и той же постоянной, которую мы обозначимбуквой N.
Таким образом, для произвольной антенны

Полученное соотношение (П.1.3), по существу, и содержит в себе искомые связи между параметрами антенны в двух режимах.
Для амплитуды тока приемной антеннывобщем случае получим
 — угол между плоскостями поляризации приемной антенны и приходящей волны. Заметим, что плоскостью поляризацииприемной антенны называется плоскость поляризации поля, излучаемого этой антенной в режимепередачи. Соотношение (П.1.3) показывает, что приемную антенну можнорассматривать как генераторс ЭДС
— угол между плоскостями поляризации приемной антенны и приходящей волны. Заметим, что плоскостью поляризацииприемной антенны называется плоскость поляризации поля, излучаемого этой антенной в режимепередачи. Соотношение (П.1.3) показывает, что приемную антенну можнорассматривать как генераторс ЭДС

и внутренним сопротивлением, равным входному сопротивлению этой антенны в режиме передачи.
Если внутреннее сопротивление этого генератора назвать входным сопротивлением антенны в режиме приема, то ZBX в режиме приема и передачи совпадают.
Диаграмма направленности приемной антенны — зависимость амплитуды ЭДС (или тока) в приемной антенне от углов и , характеризующих направление прихода плоскойэлектромагнитной волны, при постоянной величине напряженности поля в месте приема. Об этом говорит сайт https://intellect.icu . Нормированные ДН антенн в режиме приема и передачи совпадают. Фазовые ДН антенны в обоихрежимах также совпадают. Заметим, что совпадение параметров антенны в
_img_383.jpg)
_img_384.jpg)
Можно показать, что мощность отдаваемая приемной антенной в нагрузку будет составлять

 — коэффициент усиления приемной антенны.
— коэффициент усиления приемной антенны.
Как видно из (П.1.6), чембольше направленность антенны,
тем большую мощность она извлекает из поля. В выражении (П.1.6) первый множитель представляет собой плотность потока
2
мощности 5 в точке приема. Второй множитель 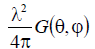 имеет размерность площади и
имеет размерность площади и
4 называется эффективной или действующей площадью антенны SФ . Тогда значение коэффициента усиления приемной антенны можноопределить по формуле

где  — геометрическая площадь антенны; — коэффициент использования поверхности.
— геометрическая площадь антенны; — коэффициент использования поверхности.
Эффективная площадь представляет собою такую площадку, которая, будучи умноженной на плотность потока мощности приходящей волны, дает мощность, отдаваемую антеннойсогласованной нагрузке при условии, что поляризации антенны и падающей волны совпадают
Соотношение (П.1.7) является одним из важнейших в теории антенн. Оно связывает эффективную площадь — параметр, удобный в режиме приема, с коэффициентом усиления
— параметром, использование которого естественно в режиме передачи. Соотношение (П.1.7) пригодно для антеннылюбой конструкции безвсяких ограничений.
Обычно наряду с (П.1.7) используют и другоесоотношение 4SФ

Для большинства антенн УКВ-диапазона потери малы, т. е.  . При этом значения SФ , определенные согласно(П.1.7) и (П.1.8), практически совпадают. Совпадают и соответствующиезначения КИП.
. При этом значения SФ , определенные согласно(П.1.7) и (П.1.8), практически совпадают. Совпадают и соответствующиезначения КИП.
Определения.
Коэффициент направленного действия приемной антенны в направлении , называется отношение мощности, поступающей на вход приемника при приеме с направления, к среднему, при приеме по всем направлениям, значению мощности, поступающей на вход приемника.
Коэффициентом усиления приемной антенны называется отношение мощности, поступающей на вход приемника при приеме на данной антенне, к мощности, поступающей на входприемника при приеме на ненаправленной антенне. При этом предполагается, что данная антенна и ненаправленная антенна согласованы с приемником и что ненаправленная антенна имеетКПД, равный единице.
Метод наведенных ЭДС был предложен Бриллуеном и Д. А. Рожанским разработан И. Г. Кляцкиным, А. А. Пистолькорсом, В. В. Татариновым и др. Этот метод может быть развит иприменительно к щелевым вибраторам (метод, наведенных МДС).
Метод наведенных ЭДС и вытекающие из него соотношения широко известны и изложены во многих монографиях. Сущность метода наведенных ЭДС заключается в следующем. Пустьимеем электрический вибратор, к которому приложена некоторая ЭДС. Под влиянием этой ЭДС в вибраторе возникает ток. Ток распределяется таким образом, что на поверхности вибраторавыполняются граничные условия, а именно условия равенства нулю тангенциальной составляющей вектора Е. Мощность излучения симметричного вибратора определяется выражением

Рассмотрим систему излучателей (рис. П.2.1).

Рис. П.2.1 — Модельвзаимного размещенияизлучателей
Граничное условие для первого излучателя
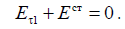
При наличии N излучающих элементов касательная составляющая для i-го элемента определяется по формуле
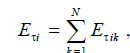
где Eik — тангенциальная составляющая вблизи i-го элемента, обусловленная полем k-го
элемента. После преобразований получим для мощности излучения следующее выражение

Тогда сопротивление излучения i-го элемента будет определятьсяпо формуле

Интеграл можно определить как некоторое вносимое сопротивление, тогда результирующая формуладля сопротивления излучения i-го элемента имеетвид

Сопротивление излучения i-го элемента определяется, как сумма произведений
отношения токов k-го элемента к рассматриваемому i-му элементу на вносимое
сопротивление 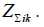
Полное сопротивление излучения для системы излучателей имеет вид

Рассмотрим пример двухэлементной антенной решетки (рис. П.2.2).

\
_img_386.jpg)
Рис. П.2.2 — Система двухактивных излучателей: а) модельвзаимного размещения излучателей; б) эквивалентная схема
Для эквивалентной схемы, приведенной на рис. П.2.2, б, тока на первом и втором излучателях будут определятьсяв ыражениями:

Рассмотрим систему двух излучателей, один из которых активный, а другой — пассивный инагруженна некоторое сопротивление (рис. П.2.3)
_img_387.jpg)

а) б) Рис. П.2.3 — Система двух излучателей: а) модельвзаимного размещенияизлучателей; б) эквивалентная схема Определить амплитуды ифазы токов в вибраторах системы излучателей, представленных на рис. П.2.3, а можно на основании эквивалентной схемы, изображенной на рисунке П.2.3,б, где введеныследующие обозначения: — возбуждающая ЭДС; Z ,
a 11
Z , Z , Z — собственные и взаимные сопротивления излучения активного и
22 12 21
пассивного вибраторов; Zí — сопротивление нагрузки. В общем случае  , а для
, а для
исследуемой антенны также 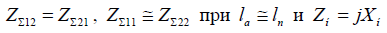 . Тогда отношение
. Тогда отношение
амплитуд и разность фаз токов в пассивном и активном вибраторах можно вычислить по следующим формулам:
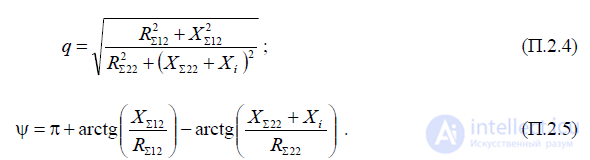
Амплитуда и фаза тока в пассивном вибраторе определяются его расстоянием до активного вибратора и настройкой, которая осуществляется изменением длины плеча вибратора.
Результирующие значения для активной и реактивной составляющей сопротивления излучения активного и пассивного излучателей определяются формулами:

Коэффициента направленного действия D можно вычислить по следующему выражению

Для определения R12 и Х12 можно использовать графики, приведенные на рис. П.2.4,
П.2.10.
_img_389.jpg)

а)
_img_390.jpg)
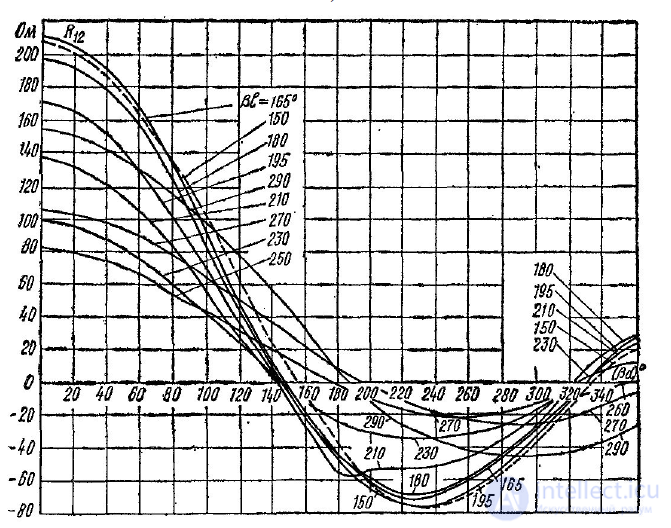
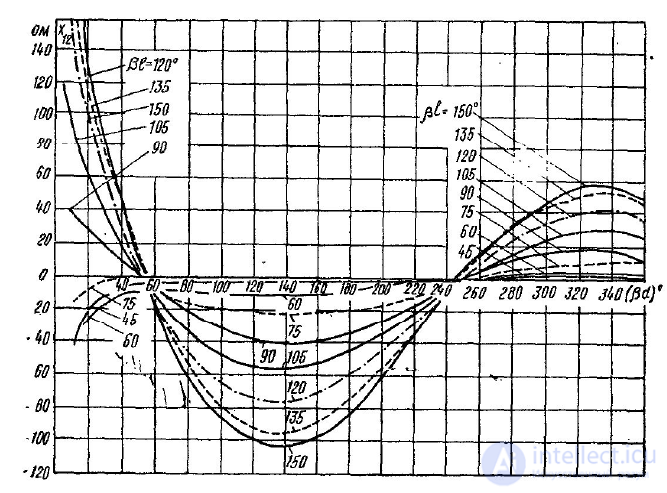
б) Рис. П.2.4 — Зависимость 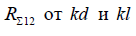
_img_391.jpg)
а)
_img_392.jpg)
б)

Рис. П.2.5 — Зависимость 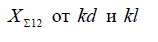
Рассмотрим двухэлементную решетку симметричных вибраторов, расположенных на оси ОY, как показано на рис. П.3.1. Пусть 1-йи 2-й излучатели расположены вдоль оси ОY. Системаотсчета угловтакже указана на рис. П.3.1.
_img_393.jpg)

Рис. П.3.1 — Схема размещенияизлучателей в решетке
Рассмотрим двухэлементную решетку излучателей, расположенных параллельно вдоль оси ОY, тогда согласно теореме умножения результирующая диаграмма направленности будет определяться выражениями:
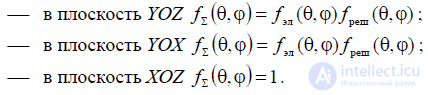
В случае размещения излучателей параллельно оси OZ (рис. П.3.1), результирующая диаграмма направленности двухэлементной решетки будет определяться выражениями:

В случае размещения излучателей параллельно оси OХ (рис. П.3.1), результирующая диаграмма направленности двухэлементной решетки будет определяться выражениями:

В качестве примера рассмотрим случай размещения излучателей параллельно оси OZ. В проекции на плоскость YOZ схемаразмещения будет выглядеть, как показано на рис. П.3.2.

Рис. П.3.2 — Проекция решетки излучателей на плоскость YOZ
На входы соответствующих симметричных вибраторов подводятся токи  и
и
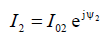 .
.
Поле излучения каждого из симметричных вибраторов, представленных на рис. П.3.2, характеризуется диаграммой направленности, которая
рассчитывается по формуле
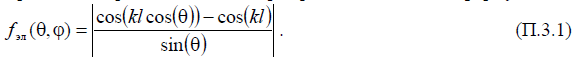
Надо отметить, что при размещении излучателей в плоскости YOХ диаграмма направленности в указанной на рис. П.3.2 системе отсчета углов определяется поформуле


Рассмотрим несколько примеров для двух излучателей, размещенных, как показано на рис. П.3.2, когда на их входыподаютсяразличные по фазетоки.
Пусть  тогда множитель решетки, диаграмма
тогда множитель решетки, диаграмма
направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть, как показано на рис. П.3.3, а.
Пусть 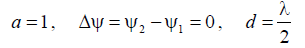 тогда множитель решетки, диаграмма
тогда множитель решетки, диаграмма
направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть, как показано на рис. П.3.3, б.
Пусть  тогда множитель решетки, диаграмма направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть,какпоказанона рис. П.3.3, в.
тогда множитель решетки, диаграмма направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть,какпоказанона рис. П.3.3, в.
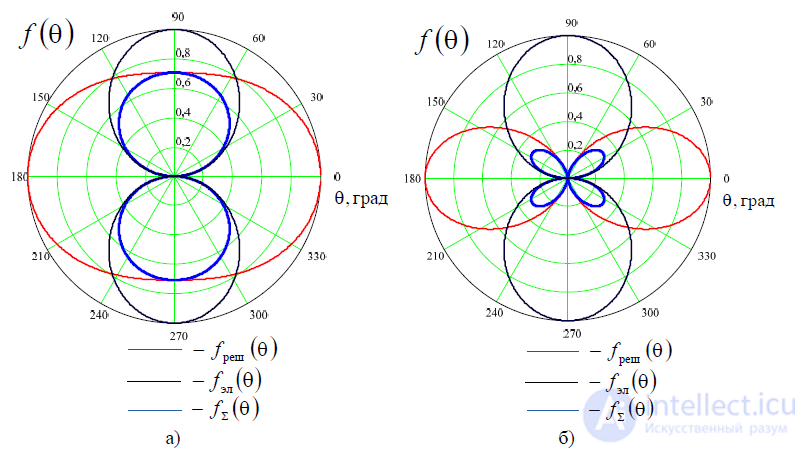

в) Рис. П.3.3 — Диаграмма направленности двухэлементной решетки симметричных вибраторов
Пусть 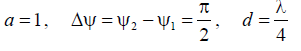 тогда множитель решетки, диаграмма
тогда множитель решетки, диаграмма
направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть, какпоказанона рис. П.3.4, а.
Пусть a 1, 2 1 , d тогда множитель решетки, диаграмма
22 направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будетвыглядеть, как показано на рис. П.3.4, б.
Пусть a 1, 2 1 , d тогда множитель решетки, диаграмма
2 направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будетвыглядеть, как показано на рис. П.3.4, в.
_img_402.jpg)

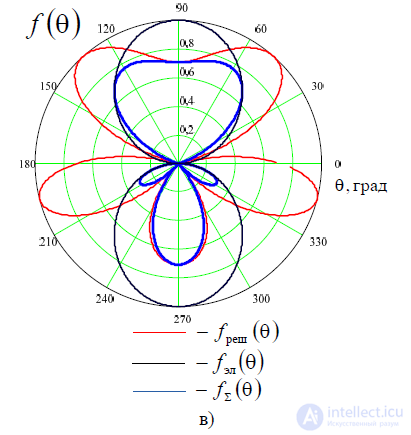
в) Рис. П.3.4 — Диаграмма направленности двухэлементной решеткисимметричных вибраторов
_img_403.jpg)
Пусть a 1, 2 1 , d тогда множитель решетки, диаграмма
4 направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть, какпоказанона рис. П.3.5, а.
Пусть a 1, , d тогда множитель решетки, диаграмма
21 2
направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будет выглядеть, какпоказанона рис. П.3.5, б.
Пусть a 1, 2 1 , d тогда множитель решетки, диаграмма направленности одного элемента и результирующая диаграмма направленности в плоскости YOZ будетвыглядеть, какпоказанона рис. П.3.5, в.

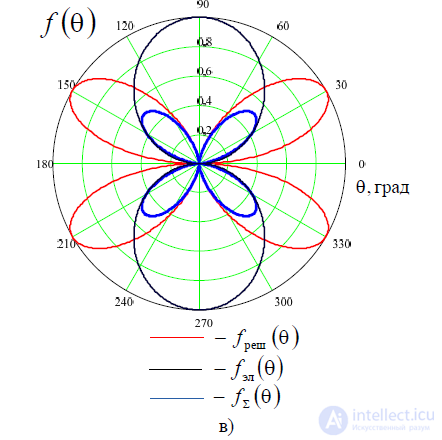
_img_406.jpg)
Таким образом, видно, что при 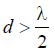 диаграмма направленности антенной решетки
диаграмма направленности антенной решетки
характеризуется наличием дифракционных максимумов. При  антенная решетка характеризуется ненаправленным излучением.
антенная решетка характеризуется ненаправленным излучением.
Наибольшая направленность
излучения обеспечивается для случая  , когда диаграмма направленности двухэлементной решетки имеет форму кардиоиды.
, когда диаграмма направленности двухэлементной решетки имеет форму кардиоиды.
Статью про теория приемных антенн я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое теория приемных антенн, Приемная антенна и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Устройства СВЧ и антенны
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Устройства СВЧ и антенны
Термины: Устройства СВЧ и антенны