Лекция
Сразу хочу сказать, что здесь никакой воды про антенны с круговой поляризацией, и только нужная информация. Для того чтобы лучше понимать что такое антенны с круговой поляризацией, поля излучения, цилиндрические антенны, конические антенны, плоские спиральные антенны, спиральная антенна, коническая спиральная антенна , настоятельно рекомендую прочитать все из категории Устройства СВЧ и антенны.
спиральная антенна — диапазонная антенна бегущей волны, основным элементом которой является проводник в форме винтовой линии или спирали. Характерной особенностью спиральных антенн является их высокое входное сопротивление. Его без использования дополнительных трансформаторов можно привести к 50 Ом для согласования с обычным коаксиальным кабелем. Применяется антенна, как правило, для приема и передачи на высоких частотах.
Спиральные антенны по особенностям конструктивного исполнения можно разделить на группы:
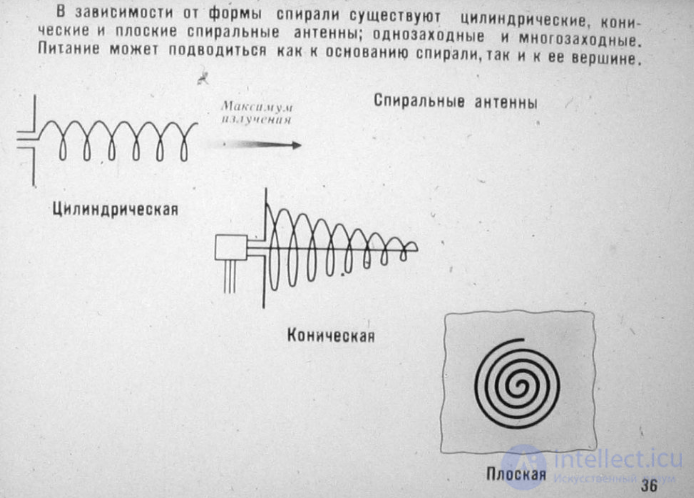

Рис. 1. Модель: а) четырехфилярная цилиндрическая винтовая антенна, б) спиральная антенна на сфере, в) плоская спиральная антенна, г) коническая спиральная антенна , д) цилиндрическая спиральная антенна.
3 дБ пропускная способность рассчитана на пять типов антенн представлены в табл.1.
|
Аntenna |
3-dB beamwidth |
|
спиральная антенна на сфере |
84 |
|
коническая спиральная антенна |
144 |
|
цилиндрическая спиральная антенна |
38 |
|
плоские спиральные антенны |
93 |
|
четырехфилярная цилиндрическая спиральная антенна. |
79 on average (unsymmetrical) |
На рис. 2 и рис. 3 показаны соответственно диаграммы направленности антенны плоской спирали и спиральной антенной на сфере.
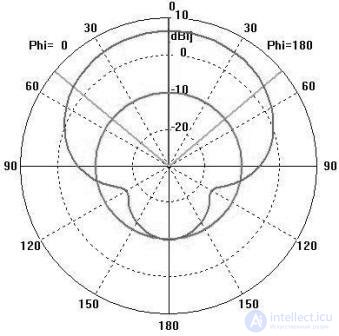
Рис. 2. Диаграмма направленности плоской спиральной антенны
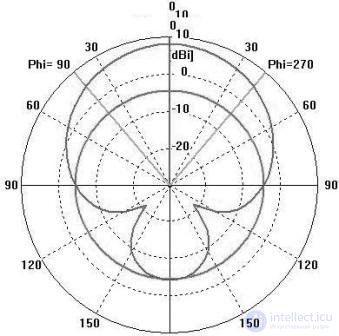
Рис. 3. Диаграмма направленности спиральной антенны на сфере
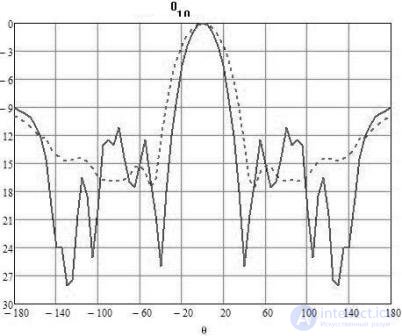
Рис. 4. Диаграмма направленности цилиндрической винтовой
антенны

Рис. 5. Осевой коэффициент для цилиндрической спиральной антенны
Теоретическая (штриховая линия) и экспериментальная (сплошная линия) диаграммы направленности конической спиральной антенны, показаны на рис. 6. Осевое соотношение по сравнению с углом показано на рис. 7.
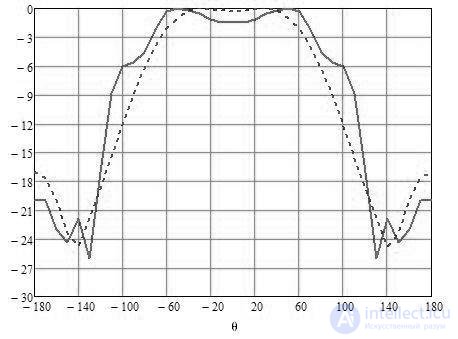
Рис. 6. Диаграмма направленности конической спиральной антенны
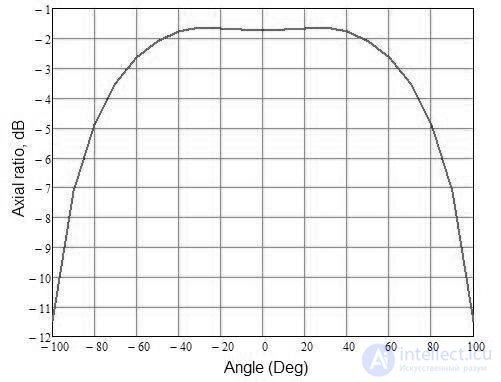
Рис. 7. Осевой коэффициент для конической винтовой антенны
Геометрия эллиптических спиральных антенн определяется габаритами образующего спираль цилиндра с поперечным сечением в виде эллипса, для которого отношение полуосей может задаваться в пределах (1…0). Если отношение полуосей эллипса равно единице, то спиральная антенна, образованная на основе цилиндра с круглым поперечным сечением называется цилиндрической спиральной антенной (ЦСА). Если отношение полуосей эллипса равно нулю, то такая плоская структура представляет собой Z-антенну. В остальных случаях структура, выполненная на цилиндре с эллиптическим поперечным сечением представляет собой эллиптическую спиральную антенну (ЭСА).
По количеству используемых излучателей спиральные антенны делятся на группы:
Главными достоинствами спиральных антенн являются:
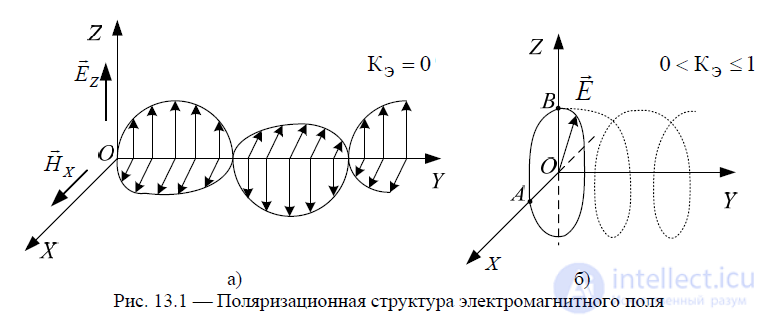
Спиральные антенны формируют поле излучения с эллиптической (или круговой) поляризацией. В отличие от поля линейно поляризованной волны (рис. 13.1, а), для которой вектор напряженности электрического поля располагается в некоторой плоскости  , в случае поля с вращающейся поляризацией при распространении электромагнитной волны вдоль оси OY вектор
, в случае поля с вращающейся поляризацией при распространении электромагнитной волны вдоль оси OY вектор 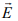 вращается вокруг этой оси с некоторой угловой частотой
вращается вокруг этой оси с некоторой угловой частотой
(рис. 13.1, б). Если при наблюдении от входных зажимов спиральной антенны вектор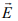 вращается по часовой стрелке, то поле считается с правосторонним вращением, иначе — с левосторонним.
вращается по часовой стрелке, то поле считается с правосторонним вращением, иначе — с левосторонним.
Одной из основных характеристик поля излучения, описывающей его поляризационную структуру является коэффициент эллиптичности, определяемый как отношение малой ОА и большой ОВ полуосей эллипса поляризации (см. рис. 13.1, б)  который может принимать значения от 0 до 1.
который может принимать значения от 0 до 1.
Наиболее общим является случай эллиптически поляризованной волны (рис. 13.2), которую можно рассматривать как результат суперпозиции двух ортогональных линейно поляризованных волн одинаковой частоты и сдвинутых по фазе на величину 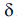 . Другой вариант представления волны с эллиптической поляризацией — это результат суперпозиции двух полей круговой поляризации одинаковой частоты, но противоположного направления вращения.
. Другой вариант представления волны с эллиптической поляризацией — это результат суперпозиции двух полей круговой поляризации одинаковой частоты, но противоположного направления вращения.
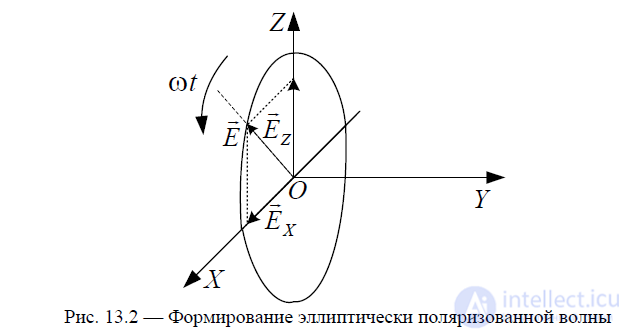
Таким образом, в соответствии с моделью электромагнитной волны, представленной на рис. 13.2, поляризационная структура поля зависит от соотношения между двумя линейными составляющими 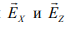 волны, распространяющейся вдоль оси OY.
волны, распространяющейся вдоль оси OY.
Линейно поляризованные составляющие поля 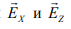 описываются выражениями:
описываются выражениями:
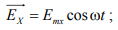
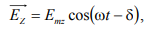
где 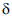 — сдвиг фаз между
— сдвиг фаз между 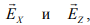
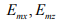 — амплитуды напряженности E поля линейно поляризованных волн, на которые раскладывается вектор (рис. Об этом говорит сайт https://intellect.icu . 13.2).
— амплитуды напряженности E поля линейно поляризованных волн, на которые раскладывается вектор (рис. Об этом говорит сайт https://intellect.icu . 13.2).
Согласно принятой модели поле эллиптической поляризации можно описать с помощью уравнения эллипса

В случае, когда 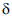 = 0, поле излучения антенны имеет чисто линейную поляризацию, которое согласно (13.1) определяется следующим соотношением
= 0, поле излучения антенны имеет чисто линейную поляризацию, которое согласно (13.1) определяется следующим соотношением
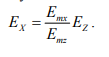
Если 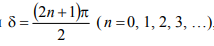 , то поле приобретает эллиптическую поляризацию
, то поле приобретает эллиптическую поляризацию
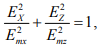
при этом полуоси эллипса ОА и ОВ совпадают с координатными осями OX и OZ, что соответствует рис. 13.1, б.
В том случае, когда амплитуды 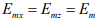 поле излучения антенны будет иметь круговую поляризацию.
поле излучения антенны будет иметь круговую поляризацию.
В случае, при котором сдвиг фаз 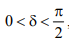 , оси эллипса ОА и ОВ, изображенного на 2 рис. 13.1, б, не будут совпадать с координатными осями.
, оси эллипса ОА и ОВ, изображенного на 2 рис. 13.1, б, не будут совпадать с координатными осями.
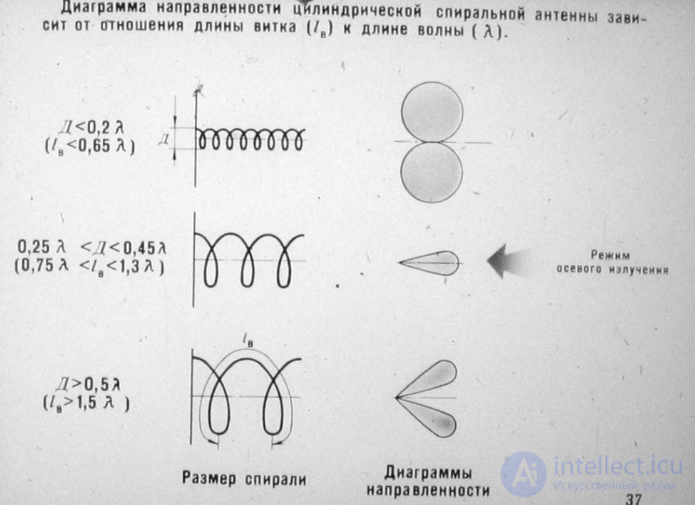
Диаграмма направленности цилиндрической антенны
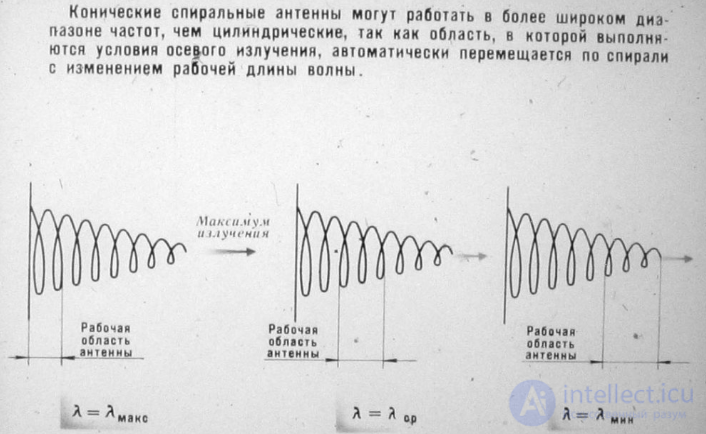


Цилиндрическая спиральная антенна (рис. 13.3) представляет собой выполненную из провода спираль 1, один конец которой свободен, а другой соединяется в точке 3 с внутреннимпроводником коаксиальной линии 4, внешний проводник которой присоединяется к металлическому экрану 2, предназначенному для ослабления обратного излученияантенны.

Рис. 13.3 — Цилиндрическая спиральная антенна:
Главными достоинствами спиральных антенн являются:
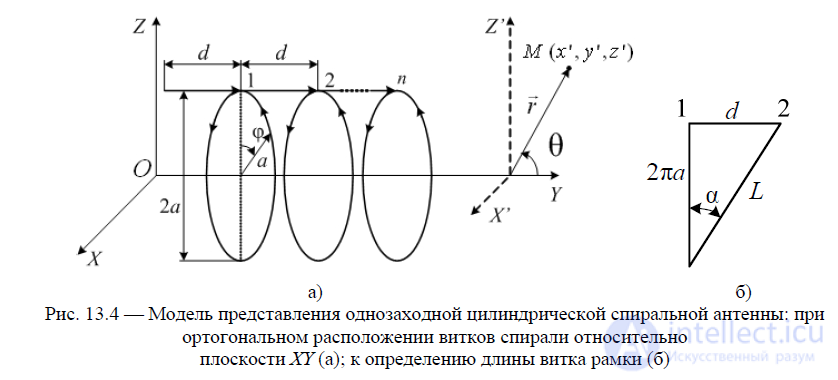
Рассмотрим характеристики поля излучения однозаходной цилиндрической спиральной антенны. Ее упрощенная модель представлена на рис. 13.4, а, б, где введены обозначения:
a — радиус спирали;
d — шаг намотки витков спирали (длина диполя);
n — число витков;
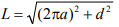 (рис. 13.4, б) — длина витка между точками «1» и «2» на рис. 13.4, а;
(рис. 13.4, б) — длина витка между точками «1» и «2» на рис. 13.4, а;
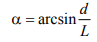 — угол наклона витков спирали относительно плоскости XОZ.
— угол наклона витков спирали относительно плоскости XОZ.
Поляризационная структура поля антенны и режим излучения зависят от соотношения геометрических параметров a , d и длины волны 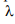 . На практике используются спиральные антенны для двух режимов работы:
. На практике используются спиральные антенны для двух режимов работы:
В случае режима ненаправленного излучения длина витка спирали меньше длины волны  . Антенну можно представить в виде системы из аксиальных кольцевых рамок и диполей с длиной, равной d <<
. Антенну можно представить в виде системы из аксиальных кольцевых рамок и диполей с длиной, равной d <<  . ЦСА работает в режиме малых рамок, поэтому суммарное поле, создаваемое антенной, имеет максимальное значение при
. ЦСА работает в режиме малых рамок, поэтому суммарное поле, создаваемое антенной, имеет максимальное значение при  (см. рис. 13.5, а). При малых по сравнению с
(см. рис. 13.5, а). При малых по сравнению с 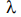 поперечных размерах антенны количество витков n не влияет на форму диаграммы направленности (ДН) и поляризационную структуру поля. Поэтому достаточно рассмотреть поле двух элементов: диполя и одного витка спирали. Так для диполя можем записать соотношение
поперечных размерах антенны количество витков n не влияет на форму диаграммы направленности (ДН) и поляризационную структуру поля. Поэтому достаточно рассмотреть поле двух элементов: диполя и одного витка спирали. Так для диполя можем записать соотношение
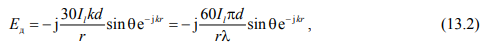
где 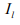 — амплитуда тока на входных зажимах диполя;
— амплитуда тока на входных зажимах диполя;
r — расстояние до точки наблюдения; 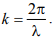
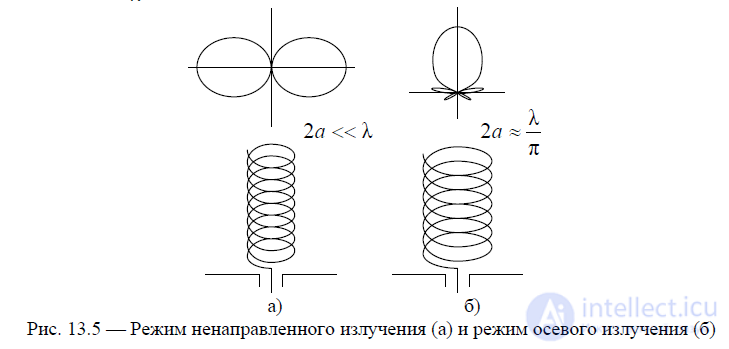
Рис. 13.5 — Режим ненаправленного излучения (а) и режим осевого излучения (б)
Для рамочного излучателя действующая длина рамки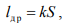 , где S — площадь рамки.
, где S — площадь рамки.
Следовательно, из (13.2) получим соотношение для поля рамки Eр в виде

где Iд — ток на действующей длине рамки.
Результирующее поле состоит из двух ортогональных компонент  (поле диполя длиной d ) и
(поле диполя длиной d ) и 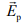 (поле рамки с периметром
(поле рамки с периметром  ).
).
В том случае, если компоненты поля будут сдвинуты по фазе на , а токи на рамке и диполе одинаковой амплитуды ( 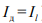 ), то
), то
коэффициент эллиптичности равен

Так из (13.4) следует, что если бы выполнялось условие 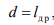 , то поле излучения в плоскости XOZ имело бы круговую поляризацию, однако на практике шаг спирали d оказывается намного меньше действующей длины рамки
, то поле излучения в плоскости XOZ имело бы круговую поляризацию, однако на практике шаг спирали d оказывается намного меньше действующей длины рамки 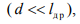 , поэтому поле характеризуется как линейно поляризованное.
, поэтому поле характеризуется как линейно поляризованное.
Рассмотрим режим осевого излучения (см. рис. 13.5, б), при котором длина витка спирали выбирается близкой к длине волны. При этом происходит синфазное или близкое к нему сложение полей витков в осевом направлении. ДН в этом случае приближается к ДН линейки излучателей, возбуждаемых в режиме бегущей волны при выполнении условия
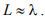 Таким образом, в режиме бегущей волны, который совпадает с режимом осевого излучения, создается поле круговой поляризации. В данном случае результирующая амплитудная ДН
Таким образом, в режиме бегущей волны, который совпадает с режимом осевого излучения, создается поле круговой поляризации. В данном случае результирующая амплитудная ДН 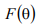 будет определяться как для решетки излучателей, возбужденных в режиме бегущей волны
будет определяться как для решетки излучателей, возбужденных в режиме бегущей волны

где 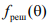 — множитель решетки, состоящей из n рамочных излучателей (рис. 13.4, а);
— множитель решетки, состоящей из n рамочных излучателей (рис. 13.4, а);
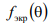 — множитель экрана;
— множитель экрана;
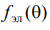 — ДН витка спирали, которую можно определять соотношением
— ДН витка спирали, которую можно определять соотношением 
Для определения 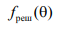 необходимо проанализировать разность фаз токов между витками «1» и «2»
необходимо проанализировать разность фаз токов между витками «1» и «2»  (см. рис. 13.4, а).
(см. рис. 13.4, а).
Для 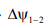 можем записать
можем записать 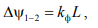
где 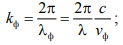
vф — фазовая скорость волны в витке;
c — скорость света в свободном пространстве.
С учетом этого

Для того чтобы излучение от всех n витков в осевом направлении складывалось, набег фазы на витке должен составлять 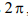 , поэтому должно выполняться условие
, поэтому должно выполняться условие
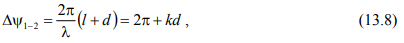
где l — периметр рамки, который должен быть близок к длине волны, kd — набег фазы на диполе (см. рис. 13.4, а).
Сравнивая (13.7) и (13.8) получим 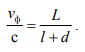
Зная, что 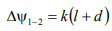 для
для 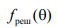 можем записать
можем записать
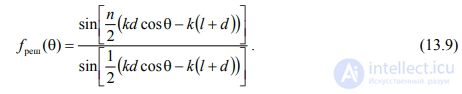
Исследуемая антенна располагается над экраном, поэтому можно воспользоваться методом зеркальных изображений.
В соответствии с этим методом при определении поля, создаваемого антенной, полагают, что она размещается над идеально проводящей поверхностью с размерами много больше длины волны.
Наводимые на поверхности плоского экрана вторичные токи исключаются из рассмотрения введением фиктивного излучателя, являющегося зеркальным изображением действительной антенны.
Зеркальный излучатель располагается на продолжении нормали, соединяющей ось симметрии реальной антенны с проводящим экраном.
В любой точке полупространства (где расположена исследуемая антенны) зеркальный излучатель создает точно такое же поле, как и реальная антенна.
С учетом сказанного при расчете ДН антенны необходимо учитывать влияние экрана, воспользовавшись множителем экрана

где — расстояние от экрана до центра решетки соосных рамочных излучателей (см. рис. 13.4, а).
Тогда результирующая амплитудная ДН антенны по полю с учетом (13.5), (13.6) и (13.9), (13.10) будет определяться выражением:

Для приближенного расчета характеристик спиральных антенн можно воспользоваться эмпирическими формулами:
— ширина ДН по уровню половинной мощности

— коэффициент направленного действия (КНД) в направлении оси спирали

— входное сопротивление

Конструкция однозаходной эллиптической спиральной антенны (рис. 13.6) должна содержать:
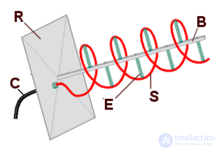

Первый телекоммуникационный спутник «Телстар» с винтообразной антенной.

Покрашенная спиральная антенна для работы с Wi-Fi шлюзом на частоте 2,5 ГГц
Несущий каркас должен быть выполнен из диэлектрического материала с малой диэлектрической проницаемостью и потерями, что снижает его влияние на характеристики излучения антенны. Внешний контур каркаса должен соответствовать внешнему контуру спиральной антенны. Структура каркаса выбирается из вариантов:
Экран выполняется круглой или квадратной формы и представляет собой сплошную металлическую поверхность. Экран должен обеспечивать уменьшение обратного излучения антенны. Габаритный размер экрана должен составлять не менее (1-3)λ. Экран располагался у основания каркаса перпендикулярно оси спирали. Центр каркаса совмещается с центром экрана.
На экране выполняется отверстие, в котором устанавливается СВЧ разъем, закрепляемый на экране с помощью винтовых соединений. К центральному проводнику разъема подключается основание спирального проводника.

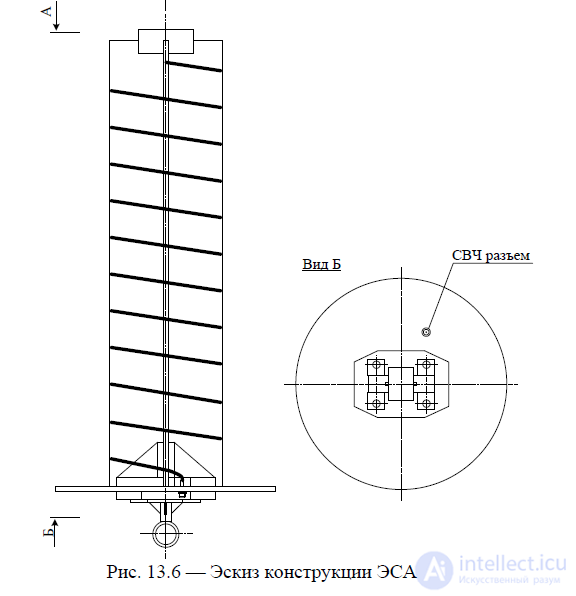
Рис. 13.6 — Эскиз конструкции ЭСА

Рисунок 2. Спиральные антенны: а) без штыря с равномерным шагом (Fixed antenna); б) с переменным шагом (более широкополосные)

Рисунок 4. Спиральная антенна в задвинутом состоянии и с выдвинутым штырем

Рисунок 9. Внутренняя часть корпуса сотового телефона с металлизированным покрытием для экранирования
Рисунок 10. Модель корпуса телефона с закрытой крышкой и вставленным штырем в поле программы IE3D
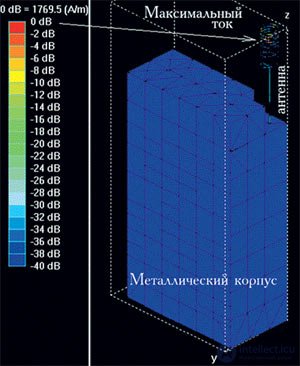
Рисунок 11. ДН в азимутальной плоскости
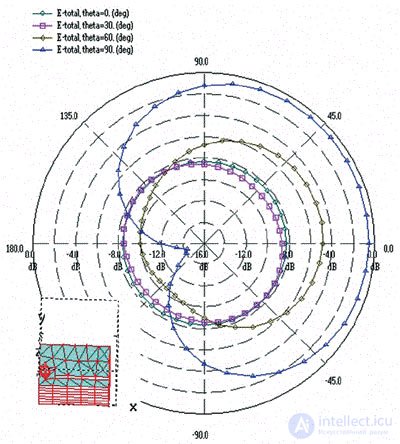
Рисунок 12. ДН в угломестной плоскости


Спиральные антенны СКАРД-Электроникс АС8.33.1-АС8.33.2 с поляризациями вида: круговая левого или правого вращения имеют широкую полосу рабочих частот 0,9 - 18 (26) ГГц и рекомендуются в качестве элемента многолучевых антенных решеток. Данные устройства поставляются в составе многолучевых антенных решеток.

рис спиральные антенны на аппарате Луноход-1
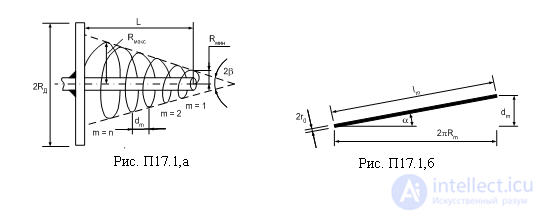
Коническая спиральная антенна (рис. П17.1,а) состоит из проволочной спирали и металлического диска. Внутренний проводник питающего коаксиального фидера присоединяется к спирали, наружная оболочка – к диску.
Конструктивные параметры спирали на рис. П17.1,а, б обозначены следующими буквами:
L – длина спирали;
Rm – радиус спирали в конце m-го витка (m = 1…n);
dm – расстояние между m и m - 1 витками спирали;
lm- длина m-го витка спирали (см. развертку m-го витка спирали на рис. П17.1,б);
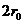 - диаметр провода спирали;
- диаметр провода спирали;
 ). Вместо ширины ДН может быть задан коэффициент направленного действия (D) антенны.
). Вместо ширины ДН может быть задан коэффициент направленного действия (D) антенны.
1. Определяются крайние длины волн рабочего диапазона
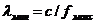 ;
;  , (П17.1)
, (П17.1)
где 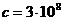 , м/с.
, м/с.
2. По заданной ширине ДН (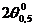 ) или КНД (D) для средней длины волны определяются: длина витка
) или КНД (D) для средней длины волны определяются: длина витка  эквивалентной цилиндрической спирали, ее осевая длина
эквивалентной цилиндрической спирали, ее осевая длина 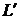 , шаг d и число витков
, шаг d и число витков 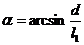 . (П17.2)
. (П17.2)
4. Угол при вершине конуса рассчитывается по формуле
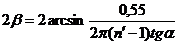 . (П17.3)
. (П17.3)
5. Число витков конической спирали определяется из выражения
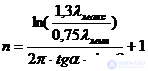 . (П17.4)
. (П17.4)
6. Осевая длина спирали рассчитывается по формуле
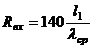 . (П17.7)
. (П17.7)
11. Производится расчет фидерной линии.
12. Общий КПД антенно-фидерной системы равен
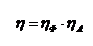 , (П17.8)
, (П17.8)
где 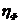 - КПД коаксиальной фидерной линии;
- КПД коаксиальной фидерной линии; 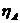 - КПД спиральной антенны, который можно принять равным 0,9…0,95.
- КПД спиральной антенны, который можно принять равным 0,9…0,95.
Статью про антенны с круговой поляризацией я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое антенны с круговой поляризацией, поля излучения, цилиндрические антенны, конические антенны, плоские спиральные антенны, спиральная антенна, коническая спиральная антенна и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Устройства СВЧ и антенны
Комментарии
Оставить комментарий
Устройства СВЧ и антенны
Термины: Устройства СВЧ и антенны