3.2. Методы восстановления счета при поражении теменных и теменно-затылочных отделов мозга

Привет, Вы узнаете о том , что такое 3.2. Методы восстановления счета при поражении теменных и теменно-затылочных отделов мозга, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 3.2. Методы восстановления счета при поражении теменных и теменно-затылочных отделов мозга , настоятельно рекомендую прочитать все из категории Нейропсихология.

Методы восстановления понимания состава числа

Краткий психологический анализ нарушения понятия числа и счета при поражении теменных отделов левого и правого полушарий мозга указывает на связь этого нарушения, с одной стороны, с дефектами пространственных представлений, а с другой — с дефектами системности восприятия и представлений. Последний дефект одинаково проявляется в интеллектуальных операциях (в счете), а при поражении левого полушария — и в речи.

В самом деле, при семантической афазии, в синдроме которой, как правило, и протекает первичная акалькулия, при поражении теменных отделов левого полушария центральным дефектом является нарушение понимания сложных логико-грамматических структур, т.е. нарушение понимания значения, которое несут не отдельные слова, а слова, вступившие в определенные связи, в систему, в то время как декодирование значения отдельных слов вне системы сложных отношений больным доступно. Принципиально тот же фактор — нарушение понимания из-за дефектов системных отношений элементов — обнаруживается и в функции счета у этой группы больных. Проявляется это прежде всего в нарушении осознания состава числа и его разрядного строения при возможности опознания отдельных цифр, а также понимания значения чисел несложного разрядного строения.

Восстанавливая понимание значения числа и умение оперировать с ним, мы тем самым способствуем восстановлению более сложных процессов — процессов системного восприятия числа. Обучение счету в этих случаях должно идти совместно с преодолением не сенсомоторных дефектов речи, а того ее уровня, который связан с кодированием и декодированием сложных системных вербальных связей, прежде всего синтагматики, а не парадигматики.

Важно отметить, что обучение счету и счетным операциям следует проводить со всеми больными с поражением теменных систем мозга, и даже с теми из них, которые не сразу обнаруживают дефекты в счетных операциях. При обследовании они нередко могут решить заданные им простые, а иногда и сложные (с переходом через десяток) примеры. Эти умения могут быть связаны с сохранностью многих упроченных и автоматизированных в прошлом опыте навыков. Однако детальное нейропсихологическое исследование состояния счета и счетных операций в процессе обучения показывает, что оставшиеся умения несистемны, отрывочны, а общая структура деятельности счета у больных оказывается пострадавшей. Эти нарушения проявляются в увеличении времени, которое требуется больным для решения примеров, в большом количестве ошибок и их специфичности, во включении речи (проговаривания) в процесс решения, в неустойчивости навыка решения арифметических примеров, в полной недоступности устного счета без опоры на зрение и т.д. Эти и другие симптомы уже указывают на необходимость восстановительного обучения больных счету.

Выше отмечалось, что на основе поражения теменных и теменно-затылочных отделов коры мозга возникает первичный распад понятия числа, нарушается осознание взаимодействия чисел внутри десятичной системы и понимание зависимости величины числа от его разрядного строения или от расположения числа в пространстве, и все это ведет к нарушению счетных операций.

Методы восстановления счета при теменно-затылочной акалькулии должны быть направлены прежде всего на восстановление понятия числа, т.е. таких его составляющих, как состав числа и его разрядное строение. С этой целью применяются следующие методы восстановительного обучения. В случаях грубейшей акалькулии иногда у больных встречается нарушение осознания связи между конкретным количеством и абстрактным числом, обозначающим количество. Тогда восстановительное обучение лучше всего начинать именно с отработки понимания количественного значения числа. Эти нарушения встречаются нередко и они характерны для больных, у которых наряду с локальными поражениями имеются и общемозговые нарушения. Этот дефект особенно часто встречается у детей младшего школьного возраста. Здесь полезны разнообразные методы, которые обеспечивают понимание соотношения чисел, написанных на карточках, с соответствующим количеством реальных предметов. Эффективными в этом случае являются метод предметности числа и метод действия с числом. Их применение способствует восстановлению осознания количественной характеристики и внутреннего состава числа. С этой целью с больным отрабатывается система десятка, понятие дополнительного числа.

Метод реализуется с помощью приема разбивки числа на части и приема именованных чисел.

Процедура. Больному дается задание разделить некое количество предметов, лежащих перед ним (например, 6), на 2 равные части (по 3). Рядом с заданным количеством предметов лежит карточка, на которой написано обозначающее его число 6, и стопка карточек, на которых написаны другие числа из первого десятка. Больной должен найти карточку с числом, соответствующим количеству каждой половины (3) и положить рядом с обозначаемым количеством. Затем больной записывает в тетрадь число 6 как 3 палочки + 3 палочки. Затем больному предлагается это же количество предметов разделить на 2 неравные группы — одна группа больше, а другая меньше. Опять повторяется та же серия операций, представляющая собой программу отрабатываемого действия: а) заданное количество разбивается на две группы; б) находятся соответствующие им числовые обозначения; в) два найденных числа сопоставляются и сравниваются с исходным числом 6; г) результат сопоставления записывается в тетрадь рядом с первой записью и т.д. Эти записи выглядят следующим образом: 6 п. = 3 п. и 3 п.; 6 п. = 4 п. и 2 п.; 6 п. = 1 п. и 5 п. (где «п.» обозначает «палочки»).

Эти действия по анализу состава числа на предметном уровне нужно проводить с числами не только первого, но и второго, а иногда и третьего десятка. Работа над осознанием состава числа с опорой на реальные предметы проводится лишь в пределах первого десятка. Анализ состава числа в пределах последующих десятков проводится уже только с абстрактным числом.

Прием: перед больным лежит карточка с заданным числом, он должен подобрать все возможные варианты чисел, составляющих заданное число, пользуясь соответствующими карточками. Серия подобных операций позволяет восстановить у больного осознание собственно числа, его состава и умение оперировать с числом без опоры на реальные предметы. Эту серию операций необходимо проводить со всеми больными, у которых имеется теменная и теменно-затылочная акалькулия, даже при отсутствии видимых грубых дефектов счета.

Для восстановления какого-либо действия, в частности умения оперировать с составом числа, важно и необходимо не только найти адекватные методы и приемы обучения, но и создать нужные условия для интериоризации заданного извне способа действия. Интериоризация — это не простое перемещение во внутренний план сознания той или другой ВПФ, а формирование этого внутреннего плана (А.Н. Леонтьев). Во внутреннем плане внешняя деятельность обнаруживает такие действия, которых нет во внешнем, т.е. во внутреннем плане происходит преобразование деятельности. Именно с этой целью мы и воссоздаем внутреннюю структуру действия, выносим ее вовне в виде серии последовательных операций. Затем постепенно переводим отрабатываемый способ выполнения действия с уровня материальной формы действия (действия с предметами) на уровень материализованный (сначала запись получаемых результатов, а позже работа с карточками, на которых написаны цифры), затем на уровень громкой речи (заданное число лишь в устной речи раскладывается на возможные комбинации чисел, составляющих его), затем это действие переводится в план шепотной речи, позже — речи «про себя». Лишь подобная форма и содержание работы может дать успех в восстановлении счета, в том числе и понимания состава числа.

Описанный дефект нередко сопровождается нарушением называния чисел, протекающим либо в синдроме амнестической афазии, и тогда больной забывает наименования чисел, либо в синдроме афферентной моторной афазии — и тогда больной не может найти соответствующего речевого (моторного) оформления числа и операций с ним. Поэтому параллельно с восстановлением понимания схемы десятка нужно вести работу над называнием числа. Изложенная выше работа уже в некоторой степени способствует восстановлению называния чисел, но поскольку этот дефект нередко бывает грубым и стойким, то необходимо обращать особое внимание на его преодоление и применять специальные методы.

Например, для этой цели может быть применен метод соотнесения слова-наименования с числом натурального ряда, где используется порядковый счет — с целью выделения отдельных слов-наименований чисел (в процессе просчитывания натурального ряда чисел) с одновременным соотнесением слова-наименования с обозначением числа, что позволяет создать нужные условия для закрепления связи число — слово (наименование). В некоторых случаях эффективным оказывается метод связи оптического изображения числа с первой буквой его наименования. Эти буквы в свою очередь вводятся в определенные слова, эмоционально близкие и знакомые больному. Например, название числа 7 нередко восстанавливается с помощью связи изображения числа 7 с буквой С (1 — С), а числа 8 с буквой В и т.д. (табл. 1). Одновременно выделенные звуко-буквы С, В желательно ввести в близкие для больного слова, например: С — Саша — сын, В — Вера — жена и т.д.

Таблица 1. Отработка наименования числа первого десятка (метод энграмм)

Восстановление называния чисел второго и третьего десятков является самостоятельной задачей, и ее решение связано с восстановлением восприятия пространственных отношений, поскольку причиной этого нарушения чаще всего являются дефекты пространственного восприятия (табл. 2).

Таблица 2. Отработка наименования числа второго десятка

Таблица 3. Обобщенная схема наименования числа

Больному предлагается схема, которая содержит правило образования слова-наименования числа и направление, в котором идет называние сложного числа (табл. 3). В таблице дается серия операций и их последовательность, которые больной должен выполнить прежде, чем назвать заданное число. Приведенная в таблице программа действий состоит из развернутой серии операций, представляющих собой способ актуализации наименования числа. Постепенно в процессе обучения этот способ сокращается по составу операций, интериоризируется с помощью постепенного перевода действия с одного уровня на другой, более высокий, и становится достоянием самого больного. После обучения больной самостоятельно 'продолжает успешно пользоваться этим способом.

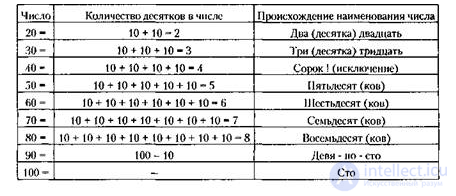
Таблица отрабатывается по частям, сначала ее первая часть, затем вторая, третья и четвертая. Отработка названий чисел в пределах каждого десятка идет все время в сравнении с наименованием чисел следующего десятка. У этих больных нередко очень затруднено понимание названия чисел, обозначающих десятки. Восстановление наименования десятков также идет путем раскрытия содержания состава числа, отраженного в его «имени». Например, схема отработки понимания названия числа 50 выглядит следующим образом: 50 = 10 + 10 + 10 + + 10 + 10 = 5 х 10 = пять десят (ков) (табл. 4).

Таблица 4. Отработка наименования десятков

Методы восстановления разрядного строения числа

Наиболее стойким и часто встречающимся дефектом при теменно-затылочной акалькулии является нарушение понимания разрядного строения числа. Поэтому на этот дефект обращается особое внимание в восстановительном обучении. Работа над восстановлением названий чисел в пределах первой сотни способствует восстановлению понимания существования двух разрядов — десятков и единиц. Больные начинают понимать, что двузначное число в пределах первой сотни состоит всегда из десятков и единиц, что и получает отражение в наименовании числа. Кроме того, они усваивают общее правило называния чисел, указывающее на то, что чтение (называние) числа всегда начинается с более высокого разряда и идет в направлении к меньшему (ср. 25,35...95). Схему называния чисел второго десятка, имеющую обратное направление — от меньшего разряда к большему (ср. 19, 15 и т.д.) больные усваивают как исключение из общего правила называния чисел. Связь названия числа с его разрядным строением используется сначала для восстановления понимания того, что каждое сложное число состоит из разных разрядов, что и отражено в его наименовании.

Метод соотнесения названия числа с его разрядным строением помогает восстановить понимание того, что в названии числа отражены все разряды и что каждый разряд имеет свое название и, наконец, что наименование разряда отражает его величину и место в разрядной сетке. Например, 125 - 100 больше 20, а 20 — больше 5. Эта работа идет обязательно совместно с восстановлением у больного понимания и количественной взаимозависимости разрядов. С этой целью проводится ряд упражнений, с помощью которых раскрываются количественное содержание числа и количественные отношения между его разрядами. С использованием этого метода проводится большое количество различных упражнений, помогающих пониманию связи разрядного строения числа с его наименованием и с количественна стороной всего числа и отдельных его разрядов.

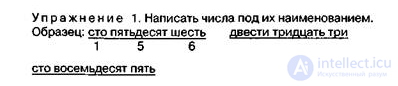
Упражнение 2. Написать наименования данных чисел.

Упражнение 3. Реконструкция числа. Дано: сто пятьдесят шесть. Из данных трех слов: а) написать возможные варианты чисел путем перестановки цифр (516, 165 и др.), б) написать их наименования, в) написать все полученные числа в строчку в порядке возрастания их величины (в порядке уменьшения), г) объяснить, как и почему отличается величина одного числа от другого.

Эти упражнения подводят к возможности работы собственно над восстановлением разрядного строения числа. Здесь можно использовать известные в литературе методы обучения детей разрядному строению числа и операциям с числами (В.В. Давыдов, 1957, 1958, 1967; Н.Н. Непомнящая, 1957, 1960). Главная задача этих методов — научить больного пониманию перехода одного разряда в другой и их количественных взаимоотношений. Первые два-три занятия (не более) проводятся с опорой на реальные предметы (так называемые этапы материализованной формы действия). В отличие от обучения детей нашим больным этот этап работы нужен лишь в качестве наглядного способа актуализации сохранившихся знаний о строении числа, а не для длительного и последовательного обучения этому, как это имеет место у детей. В течение нескольких занятий больной работает над самостоятельным разложением заданного ему количества предметов (палочек, спичек и т.д.) на разряды, опираясь при этом на знания о том, сколько и какие единицы входят в каждый разряд. Например, больному дается 15 палочек и задание — разложить их на десятки и единицы. Больной откладывает 10 палочек налево и 5 направо. Десяток палочек он заменяет картонным квадратиком, который и будет впредь обозначать один десяток, и к нему придвигает 5 палочек, которые обозначают единицы; после этого больной называет заданное число и записывает его в тетрадь, а в разрядную сетку записывает развернутую схему его построения:

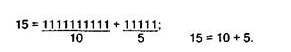
Такую серию операций больной выполняет и с числами второго десятка. Больному даются любые числа второго десятка (25, 28 и т.д.), и он должен таким же образом развернуть их количественное содержание: налево отложить отдельно друг от друга 2 десятка палочек, затем заменить их двумя картонными квадратами, придвинуть к ним оставшееся количество единиц, сделать соответствующие записи и т.д. После прочного усвоения принятого построения двузначного числа проводятся упражнения с трехзначным числом, т.е. с числом, состоящим из трех разрядов. Здесь счет идет сразу по десяткам. Больные к этому времени обычно уже знают, что 100 состоит из 10 десятков. Поэтому они сначала вместо нужного количества палочек («единиц») кладут слева 10 квадратиков, обозначающих вместе сотню, а затем заменяют их спичечной коробкой, в которую кладут все 10 квадратиков. И коробка с этого момента обозначает 1 сотню или 10 десятков. При задании составить число 123 больные кладут 1 спичечную коробку, обозначающую сотню, 2 пуговицы, обозначающие десятки, и 3 спички (палочки), обозначающие единицы (табл. 5).

Таблица 5. Восстановление разрядного строения числа

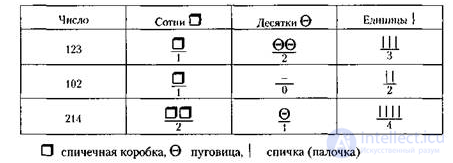
Эти упражнения очень полезны, но им не следует отводить много времени. После усвоения общего принципа построения числа надо сразу переходить к работе с числом без опоры на его количественную сторону, для чего использовать разрядную сетку.

Метод разрядной сетки включает в себя ряд приемов и упражнений, которые помогают освоить и закрепить восстанавливаемое действие или психический процесс. Цель — восстановить понимание разрядного строения числа. Приемы предварительной работы над числом вне разрядной сетки:

1) анализ и разбор заданных чисел по разрядам вне разрядной сетки,

2) прием заполнения пустого места (разряда) в числе, т.е. прием восстановления понимания значения нуля,

3) прием перестановки цифр в одном и том же числе для получения новых чисел,

4) прием сравнительного анализа полученных чисел (разрядного количественного).

После закрепления полученных навыков можно переходить к работе с собственно разрядной сеткой. И здесь возможны самые различные упражнения. Например, вписывание в разрядную сетку задаваемых чисел, строго придерживаясь разрядов. Пониманию соотношения разрядов в числе очень помогают упражнения, в которых больному даны одни и те же (или одна) цифры, которые путем вписывания их в разрядную сетку превращаются в число и каждый раз в другое (по своей количественной сущности) в зависимости от места, которое они занимают в этой сетке. Об этом говорит сайт https://intellect.icu . Например, больному даются две цифры — 1 и 2. Он проставляет их в сетку и называет полученные числа. Пустые клетки сначала не заполняются и ставится прочерк. А затем идет работа над значением нуля в числе, отрабатывается понимание количественной сущности нуля как указателя на отсутствие количества в каком-либо разряде (105; 150). И после этого прочерки (черточки) в числах замещаются нулем (табл. 6).

Таблица 6. Восстановление разрядного строения числа

С помощью этих приемов и упражнений у больного восстанавливается осознание зависимости значения числа от его места в разрядной сетке, т.е. в пространстве, восстанавливается также и понимание значения и места нуля в записи числа. Эти знания закрепляются в целом ряде упражнений, в которых от больного снова требуется анализ разрядов заданного числа, снова вне разрядной сетки. Для этого больной должен выполнить следующие задания: а) назвать разряды, из которых состоит заданное число, б) показать вразброс, где десятки, тысячи, единицы и т.д. в данном числе, в) составить двузначное или любое другое сложное число, г) назвать пропущенный в данном числе разряд (1 -595, 1-5, -6 и т.п.), д) написать в столбик друг под другом заданные числа 25, 384, 108, 10590 и прочитать число и т.д.

Существует еще множество разнообразных методов, приемов и упражнений для восстановления понимания разрядного строения числа, но принцип построения методов один и тот же. Для всех этих методов характерна общая направленность на восстановление осознания больными зависимости значения знака (числа) от его места в пространстве.

Итак, описанная нами работа по восстановлению счета и счетных операций включает обучение больных: а) пониманию состава числа, взаимозависимости чисел, их системности и целостности, б) называнию чисел, в) пониманию связи наименования с разрядным строением и количественной стороной числа, г) пониманию собственно разрядного строения числа и зависимости величины числа от его положения в пространстве. Все это и ведет к восстановлению понятия числа и создает основу для восстановления счислительных операций.

Методы восстановления счетных операций

Нарушение понятия числа не может не привести к дефектам счетных операций, поскольку выполнение арифметических действий сложения, вычитания, умножения и деления требует знания разрядного строения числа, схемы десятка, т.е. умения дополнять одно число другим в пределах десятка и т.д. Для правильного протекания процесса счета необходима также сохранность и пространственных представлений о направлении отнимания и прибавления. У больных описываемой группы счетные операции нарушаются именно в связи с дефектами обоих указанных звеньев в структуре арифметических действий.

Обучение больных счетным операциям требует длительной и направленной работы и начинается уже при работе над восстановлением понятия числа. Здесь больных, как мы видели, учат расчленению числа на составные части (состав числа), дополнению числа в пределах десятка. На этой же стадии больные обучаются и осознанному отношению к разрядному строению числа, пониманию места и значения нуля. Все это создает необходимые условия для восстановления счетных операций.

Специальное обучение больных счету (выполнению арифметических действий) лучше начинать с более простых и менее всего пострадавших операций сначала в пределах первого десятка, затем второго. Операции сложения и вычитания проводятся без перехода через десяток, а умножение и деление производятся на простейших однозначных и двузначных числах. Эта работа занимает 3—5 занятий. Трудности восстановительного обучения с применением разнообразных творческих методов и приемов начинаются при обучении больных вычитанию и сложению с переходом через десяток. Действие сложения или вычитания в пределах одного десятка является по своему составу простым, состоящим из одной операции (ср.: 10 - 2 = 8, 15 -5 = 10, 15 + 2 = 17, 23 - 3 = 20 и т.д.), так же, как и операции с «круглыми» числами (10+ 10,20- 10,50-40 + 10). Те же арифметические действия с числами, требующими перехода через десяток, являются по своему математическому и психологическому составу более сложными: они включают несколько операций. Исследование навыков счета у больных этой группы показало, что у них прежде всего нарушена способность совершать именно эти арифметические действия, требующие анализа пространственных схем. Эти больные не всегда в состоянии осознанно расчленить арифметическое действие на составляющие его операции. Преодоление этого дефекта и является основной задачей следующей стадии обучения. К этому времени больные уже должны знать схему десятка и уметь расчленять число на его составные части, уметь округлять числа до ближайшего десятка (ср.: 18(+2) = 20; 12(-2) = 10). Работу над восстановлением операций «округления» чисел необходимо провести до этой стадии обучения, поскольку при решении арифметических примеров с переходом через десяток они выступают в качестве конкретных звеньев в структуре решения.

Есть разные способы округления числа до десятка. Поэтому сначала надо провести ряд занятий по актуализации больным «своего» способа. С этой целью больной обучается разным способам округления, и по эффективности выполнения (более точный счет, затрата меньшего времени, уверенность в действиях и т.д.) можно судить о более доступном больному способе (или об актуализации его собственного способа).

Например, 15-7. 1-й способ: 7 = 5 + 2 (округление до 5), 2-й способ: 7 + 3 = 10 (округление до 10). Работу надо начинать с помощью метода восстановления состава числа (см. выше), используя прием сравнения величины чисел.

Задание. Указать, какое число больше или меньше (поставить соответствующий знак): 8 ... 10; 7 ... 10; 10 ... 6; 20 ... 17; 15 ... 20 и т.д. Прием количественной оценки разницы чисел (числа даются те же). Дано: 8 и 10. Выполнение больным: 8 < 10. Вопрос: на сколько единиц? «На 2»; дано: 20 и 17; 20 > 17. На сколько единиц? «На 3». Прием округления числа. Задание: округлить число 17 до 20. Операция: 17 + 3 = 20.

На этой стадии работу нужно вести только с числами и на речевом уровне.

После обучения больного понятию числа и конкретным операциям «округления» чисел можно переходить к работе над осознанием больным пооперационного решения арифметического примера. К этому времени больной уже понимает, благодаря отработанному ранее умению, что при выполнении действий с числами с переходом через десяток второе число (вычитаемое или слагаемое) нужно разбить на два составляющих его числа (путем округления), которые потом последовательно вводятся в соответствующие операции, составляющие содержание арифметического действия. Исходя из этого понимания, больных обучают разбивать арифметическое действие на последовательные операции — сначала в вербальном плане: больной совместно с педагогом, а потом самостоятельно пишет программу операций: а) округлить число, б) вычесть (или прибавить) одну часть числа, в) сложить (или вычесть) вторую часть числа. Затем программа реализуется. Дается пример: 52 - 18. Больной проделывает все операции по вербальной программе, выполняя каждую операцию и одновременно проговаривая: а) «я округляю число 18 до 20. 18(+2) = 20; б) теперь нужно вычесть полученное число, это одна часть от 18(+2) = 20; 52 - 20 = 32; в) а теперь прибавляю вторую часть числа 32 + 2 = 34».\

Не менее эффективным является обучение способу решения подобных примеров, который требует от больных умения приравнивать единицы вычитаемого (или слагаемого) к единицам уменьшаемого (или первого слагаемого). Тогда состав операции приобретает следующий вид.

Сверху пишется памятка: во второй и третьей операциях нужно вычитать или прибавлять:

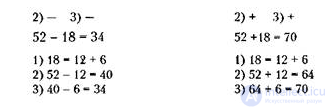
Обучение решению арифметических примеров на сложение и вычитание с переходом через десяток следует начинать с максимально развернутого действия с одновременным громким проговариванием решения и с опорой на внешние средства — схемы, записи. Позже, после закрепления этой формы действия, можно переходить к постепенному сокращению действия за счет изъятия из записи первой операции и перевода ее на уровень громкой речи, т.е.

продолжение следует...

Продолжение:

Часть 1 3.2. Методы восстановления счета при поражении теменных и теменно-затылочных отделов мозга
Часть 2 - 3.2. Методы восстановления счета при поражении теменных и теменно-затылочных
Часть 3 - 3.2. Методы восстановления счета при поражении теменных и теменно-затылочных