Лекция
Сразу хочу сказать, что здесь никакой воды про теория фильтров, и только нужная информация. Для того чтобы лучше понимать что такое теория фильтров, фильры сигналов, фильтр, влияние фильтра на параметры импульса , настоятельно рекомендую прочитать все из категории Устройства СВЧ и антенны.
фильтр в электронике — устройство для выделения желательных компонентов спектра электрического сигнала и/или подавления нежелательных.
Фильтры — неотъемлемая часть многих СВЧ устройств. Они используются для целей разделения и суммирования сигналов с различными частотами в многоканальных устройствах, в преобразователях и умножителях частоты, для повышения избирательности приемных устройств, для ограничения спектра передатчика и т. д.
Столь широкое применение фильтров в технике СВЧ привело к большому многообразию их схем и конструкций. Наибольшее распространение нашли фильтры СВЧ, полученные из низкочастотных фильтров путем замены элементов с сосредоточенными параметрами элементами СВЧ устройств, обладающих теми же характеристиками в определенной области частот.
Фильтры — неотъемлемая часть многих СВЧ устройств. Они используются для целей разделения и суммирования сигналов с различными частотами в многоканальных устройствах, в преобразователях и умножителях частоты, для повышения избирательности приемных устройств, для ограничения спектра передатчика и т. д.
Столь широкое применение фильтров в технике СВЧ привело к большому многообразию их схем и конструкций. Наибольшее распространение нашли фильтры СВЧ, полученные из низкочастотных фильтров путем замены элементов с сосредоточенными параметрами элементами СВЧ устройств, обладающих теми же характеристиками в определенной области частот.

Фильтры СВЧ, как и фильтры с сосредоточенными параметрами, представляют собой один или N последовательно соединенных четырехполюсников, избирательно пропускающих определенную полосу частот. В зависимости от полосы пропускания фильтры разделяются на следующие типы:
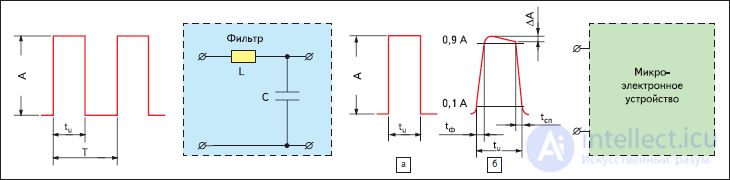
фильтры нижних частот (ФНЧ), пропускающие частоты от нуля до частоты среза - f1 (рис 4.1, а);
фильтры верхних частот (ФВЧ), пропускающие частоты от f1 до 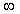 (рис.4.1, б);
(рис.4.1, б);
полосовые фильтры (ПФ), пропускающие определенную полосу частот от f-nдо fn(рис. 4.1, в);
заграждающие (режекторные) фильтры (ЗФ), не пропускающие полосу частот от f-з до fз (рис. 4.1, г).
Фильтры, находящие применение в обработке сигналов, бывают
Среди множества рекурсивных фильтров отдельно выделяют следующие фильтры (по виду передаточной функции):
По порядку (степени уравнения) передаточной функции ( ЛАФЧХ) различают фильтры первого, второго и более высоких порядков . Крутизна ЛАЧХ фильтра 1-го порядка в полосе подавления равна 20 дБ на декаду, фильтра 2-го порядка — 40 дБ на декаду, и т. д.
По тому, какие частоты фильтром пропускаются (задерживаются), фильтры подразделяются на
В конструкциях пассивных аналоговых фильтров используют сосредоточенные или распределенные реактивные элементы, такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя их, можно добиться усиления или ослабления гармоник с нужными частотами. Другой принцип построения пассивных аналоговых фильтров — это использование механических (акустических) колебаний в механическом резонаторе той или иной конструкции.
В качестве простейших фильтров низких и высоких частот могут использоваться RC-цепь или LR-цепь. Однако они имеют невысокую крутизну АЧХ в полосе подавления, недостаточную во многих случаях: всего 6 дБ на октаву (или 20 дБ на декаду) — для RC-фильтра, являющегося фильтром 1-го порядка и 40 дБ/декада для LC-фильтра, являющегося фильтром 2-го порядка. В пассивных фильтрах добавление в схему фильтра любого реактивного компонента увеличивает порядок фильтра на 1.
Простейший фильтр нижних частот 1-го порядка изображен на рисунке и состоит из последовательно соединенных резистора и конденсатора
, образующего делитель напряжения входного сигнала. Комплексный коэффициент передачи
такого делителя:
где — постоянная времени RС-цепи.
Модуль коэффициента передачи этой цепи:
где
При входной частоте модуль коэффициента передачи близок к 1, при
модуль коэффициента передачи близок к 0, на частоте
модуль коэффициента передачи равен
— уменьшение относительно единичного коэффициента передачи приблизительно на 3,01 дБ, эта частота называется частотой среза фильтра. В полосе подавления при частоте много выше частоты среза модуль коэффициента передачи уменьшается на 20 дБ на декаду изменения частоты.
На рисунке показан пример простейшего LC-фильтра нижних частот 2-го порядка: при подаче гармонического сигнала определенной частоты на вход фильтра (на рисунке слева) напряжение на выходе фильтра (справа) в установившемся режиме определяется отношением реактивных сопротивлений катушки индуктивности () и конденсатора (
).
Коэффициент передачи ФНЧ можно вычислить, рассматривая этот фильтр как делитель напряжения, образованный реактивными сопротивлениями.
Комплексное (с учетом сдвига фаз между напряжением и током) сопротивление катушки индуктивности есть и комплексное сопротивление конденсатора
, где
— мнимая единица,
— угловая частота входного гармонического сигнала, поэтому для ненагруженного LC-фильтра коэффициент передачи
будет выражаться формулой для делителя напряжения:
.
Подставляя в формулу выражения для комплексных сопротивлений, получим для частотно-зависимого коэффициента передачи:
.
Как видно, коэффициент передачи ненагруженного идеального ФНЧ источником сигнала для которого является идеальный генератор напряжения с нулевым внутренним сопротивлением неограниченно растет с приближением к резонансной частоте , так как знаменатель выражения стремится к нулю. Об этом говорит сайт https://intellect.icu . При повышении частоты выше резонансной — убывает. На очень низких частотах коэффициент передачи ФНЧ близок к единице, на очень высоких — к нулю.
Принято называть зависимость модуля комплексного коэффициента передачи фильтра от частоты амлитудно-частотной характеристикой (АЧХ), а зависимость фазы от частоты — фазо-частотной характеристикой (ФЧХ).
В реальных схемах к выходу фильтра подключается активная нагрузка , которая понижает добротность фильтра и устраняет острый всплеск коэффициента передачи вблизи частоты резонанса .
Величину называют характеристическим сопротивлением фильтра или волновым сопротивлением фильтра. Если ФНЧ нагрузить на активное сопротивление, равное характеристическому, то передаточная функция станет нерезонансной, коэффициент передачи будет примерно постоянный для частот
, и убывающий как
на частотах выше
. На частоте
коэффициент передачи такого ФНЧ уменьшается на 3 дБ относительно значения коэффициента передачи на низкой частоте, эту частоту называют частотой среза фильтра. На частотах много выше частоты среза коэффициент передачи уменьшается на 40 дБ на декаду изменения частоты.
Аналогичным образом строится и LC-фильтр верхних частот. В схеме ФВЧ меняются местами катушка индуктивности и конденсатор. Для ненагруженного ФВЧ получается выражение для коэффициента передачи:
.
На очень низких частотах модуль коэффициента передачи ФВЧ близок к нулю. На очень высоких — к единице.
На сверхвысоких частотах сосредоточенные элементы (конденсаторы и катушки индуктивности) практически не используются, так как с ростом частоты их типичные для этого диапазона номиналы, а следовательно и габариты, уменьшаются настолько, что изготовление их становится невозможным. Поэтому применяются так называемые линии с распределенными параметрами, в которых индуктивность, емкость и активная нагрузка равномерно или неравномерно распределены по всей линии. Так, элементарный ФНЧ, рассматриваемый в предыдущем разделе, состоит из двух сосредоточенных элементов, представляющих собой резонатор; в случае же распределенных параметров фильтр будет состоять из одного элемента-резонатора (например отрезка микрополосковой линии или металлического стержня).
Конструкции СВЧ фильтров весьма разнообразны, и выбор конкретной реализации зависит от предъявляемых к устройству требований (значение рабочих частот, добротность, максимальное затухание в полосе задержания, расположение паразитных полос пропускания).
Проектирование фильтров на распределенных параметрах является достаточно сложным процессом, состоящим из двух этапов: получение электрических параметров, исходя из требований к устройству; получение габаритных параметров из полученных электрических. В основе современных методов проектирования микроволновых фильтров лежит теория связанных резонаторов.
Электромеханический фильтр (ЭМФ) содержит механическую резонансную систему (резонатор) той или иной конструкции. На входе и на выходе фильтра стоят электромеханические преобразователи, которые преобразуют электрические колебания сигнала в механические колебания рабочего тела фильтра и обратно.
ЭМФ получили распространение в трактах промежуточной частоты высококачественных радиосистем (в том числе военных, морских, радиолюбительских и других). Их преимуществом является значительно бо́льшая, чем у эквивалентных LC-фильтров, добротность, позволяющая достичь высокой избирательности, необходимой для разделения близких по частоте радиосигналов в приемниках.
Активные аналоговые фильтры строятся на основе усилителей, охваченных петлей обратной связи (положительной или отрицательной). В активных фильтрах возможно избежать применения катушек индуктивности, что позволяет уменьшить физические размеры устройств, упростить и удешевить их изготовление.
Фильтр нижних частот представляет собой четырехполюсник типа С, LС, Т или Pi с реактивными элементами . В таких электрических цепях имеют место переходные процессы при прохождении импульсов. Ток в индуктивности не может изменяться скачком, поэтому в момент падения импульса индуктивность подобна разрыву цепи в месте ее включения. По мере нарастания тока ее действие все больше соответствует короткому замыканию. На емкости же не может изменяться скачком напряжение. Поэтому в первый момент она оказывает действие, подобное короткому замыканию между точками ее включения. По мере того как емкость заряжается, ток через нее уменьшается. При полной зарядке емкость аналогична разрыву.
Совместное действие этих процессов вызывает искажение формы импульса: появление времен фронта tф и спада tсп и изменение амплитуды ΔА (рис. 1). Время фронта и спада принято отсчитывать по уровню амплитуды 0,9 А и 0,1 А.
На рис. 1 в качестве примера показаны входные прямоугольные импульсы. Получить идеальные прямоугольные импульсы технически сложно. Реальные импульсы имеют форму, близкую к трапецеидальной. При конструировании фильтра необходимо выбрать его индуктивность и, особенно, емкость такими, чтобы искажение формы импульса было минимальным. Для этого нестационарные явления, вызванные в электрической цепи фильтра воздействием данного импульса, должны полностью заканчиваться к началу следующего импульса. В общем виде это требование к фильтру можно сформулировать следующим образом: постоянная времени электрической цепи фильтра должна быть меньше, чем длительность импульсов. На практике это означает, что емкость и индуктивность фильтра должны быть минимальными.
Практически такие идеальные частотные характеристики неосуществимы, поэтому при проектировании фильтров задаются отклонения от этих идеальных характеристик.
Каждый фильтр характеризуется следующими параметрами:
граничные частоты полосы пропускания f-n, fn (для ФНЧ и ФВЧ —
частоты среза f1);
граничные частоты полосы загражденияf-з, fз;
максимально допустимое затухание в полосе пропускания - bn, дб;
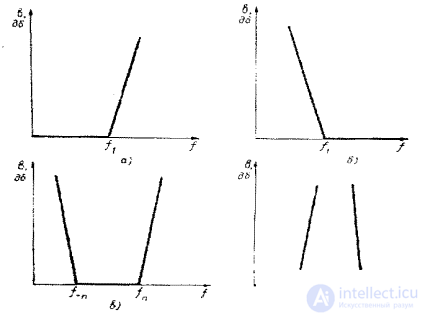
Рис. 4.1.Идеальные частотные характеристики фильтров:
а - ФНЧ; б - ФВЧ; в - ПФ; г - ЗФ.
минимальное затухание на границах полосы заграждения - bn, дб;
номинальное характеристическое сопротивление, выбираемое из конструктивных соображений.
В зависимости от предъявляемых требований к фильтру применяются различные схемы фильтров и разнообразное их конструктивное выполнение. У полосовых фильтров наибольшее распространение получили следующие схемы звеньев:
трехэлементная схема (рис. 4.2, а, Т-образная схема);
четырехэлементная схема (рис. 4.2, б, П-образная схема}.
Каскадное соединение этих звеньев образует общую лестничную структуру фильтра (рис. 4.2, в, г).
Задачей проектирования является обеспечение требуемой полосы пропускания, допустимых уровней затухания в полосе пропускания, обеспечение требуемого динамического диапазона, минимального веса и габаритов, сохранение работоспособности в ухудшенных климатических условиях, простоты настройки и изготовления и максимальной надежности.
Существуют два метода расчета фильтров:
по характеристическим параметрам;
по рабочим параметрам.
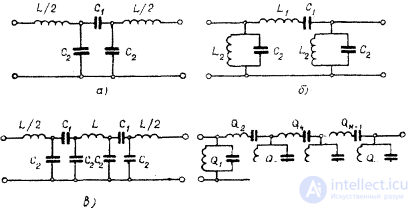
Рис. 4.2.Схемы фильтров: а —трехэлементная схема звена;
б — четырехэлементная схема звена;в, г —- лестничные схемы фильтров трех- и четырехэлементные соответственно.
Все расчеты по характеристическим параметрам являются частными случаями расчетов по рабочим параметрам, а следовательно, более просты. Метод расчета по характеристическим параметрам применяется в том случае, если допускается значительная неравномерность характеристики частотного затухания фильтра в полосе прозрачности. В этом случае фильтр состоит из N одинаковых звеньев. Параметром является характеристическое сопротивление фильтра, выбираемое из конструктивных соображений и используемое для определения элементов схемы фильтра. По методу характеристических параметров рассчитываетсятрехэлементная схема (рис. 4.2, а, в), выполненная на коаксиальных линиях и получившая наибольшее практическое распространение.
Метод расчета по рабочим параметрам позволяет получить заданную частотную характеристику фильтра при минимальном числе элементов, исходя из условий физической реализуемости. В качестве рабочих параметров используются следующие: требуемая полоса пропускания — f-n>fn; максимально допустимое затухание в полосе пропускания — bn; минимально допустимое затухание в полосе заграждения — bз. Требуемая частотная характеристика затухания аппроксимируется физически реализуемой функцией, через параметры которой определяются элементы схемы фильтра.
Существует несколько способов аппроксимации:
Наибольшее распространение получили первые два способа аппроксимации.
При аппроксимации с помощью максимально гладкой (плоской) кривой частотная характеристика полосового фильтра имеет вид, показанный на рис.4.3, а (парабола 2 N-го порядка). В этом случае частотная характеристика описывается формулой 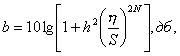
где
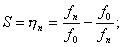 (4.2)
(4.2)
S - масштабный множитель,
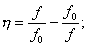 (4.3)
(4.3)
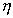 - частотная переменная;
- частотная переменная;
f0 - средняя частота диапазона;
N - число звеньев фильтра;
h - амплитудный множитель;
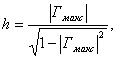 (4.4)
(4.4)
Гмакс - максимально допустимый коэффициент отражения в полосе f-n>fn, связанный с максимально допустимыми потерями в полосе пропускания формулой
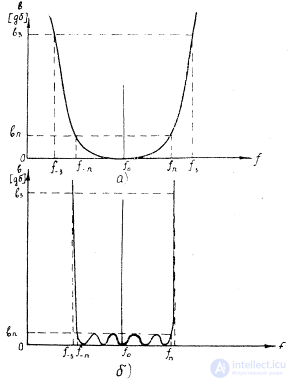
Рис. 4.3. Частотные характеристики полиномиальных полосовыхфильтров: а - максимально гладкая; б - чебышевская.
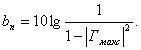 (4.5)
(4.5)
При аппроксимации с помощью полиномов Чебышева частотная характеристика имеет вид, показанный на рис.4.3, б. В этом случае частотная характеристика описывается формулой
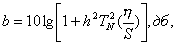 (4.6)
(4.6)
где 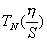 -полином Чебышева 1-го рода, N-го порядка, (2.9) - (2.12);
-полином Чебышева 1-го рода, N-го порядка, (2.9) - (2.12);
N — число звеньев фильтра.
Чебышевские фильтры имеют более крутые склоны частотной характеристики, чем фильтры с максимально гладкой характеристикой. Выбор того или иного типа частотной характеристики определяется заданными требованиями к фильтру. По выбранному типу частотной характеристики и заданным f-n, fn,f-з, fз, bn, bз определяется число звеньев фильтра N.
Для полосового фильтра число звеньев определяется по формулам:
для максимально гладкого фильтра
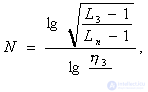 (4.7)
(4.7)
где Lз, Lп - коэффициенты передач, определяемые из формул

для чебышевского фильтра  (4.8)
(4.8)
Следующим этапом синтеза является определение численных значений элементов схемы фильтра. Для упрощения методики расчета по рабочим параметрам используется нормализованный расчет, то есть для «прототипа» — фильтра нижних частот (рис. 4.4), из которого можно получить элементы схемы проектируемого фильтра.
Элементы «прототипного» ФНЧ для фильтров с максимально гладкой характеристикой определяются по формуле
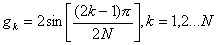 (4.9)
(4.9)
Для фильтра с чебышевской формой характеристики элементы прототипа определяются из следующих выражений:
1) для нечетных 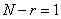 ,
,
для четных 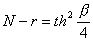 ,
,
2) 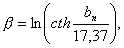
где bn — максимально допустимая пульсация в полосе пропускания фильтра, дб (рис. 4.3);
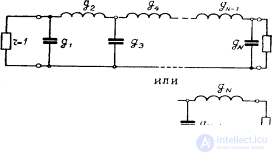
Рис. 4.4. Схема прототипа фильтра нижних частот для четных и нечетных N.
3) 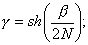
4) 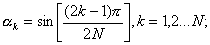
5)  (4.10)
(4.10)
6) 
7) 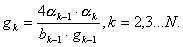
Приведенные формулы выведены при следующих предположениях:
1. Сопротивление нагрузки в левой части схемы равно 1 Ому.
2. Первый элемент g1 — шунтирующая емкость в фарадах, последовательные элементы — индуктивности в генри.
3. Сопротивление r в правой части схемы равно 1 Ому для всех рассматриваемых случаев. Исключение представляют чебышевские фильтры с четным N.
Элементы схем других фильтров определяются через известные элементы прототипа путем соответствующих преобразований. Формулы для этих преобразовании разработаны для конкретныхсхем.
После расчета элементов фильтра остается задача его реализации с помощью элементов СВЧ. Методы реализации фильтров с помощью элементов СВЧ будут освещены в следующих разделах при рассмотрении типичных схем фильтров.
LC-фильтры используются в силовых электрических цепях для гашения помех и для сглаживания пульсаций напряжения после выпрямителя. В каскадах радиоэлектронной аппаратуры часто применяются перестраиваемые LC-фильтры, например, простейший LC-контур, включенный на входе средневолнового радиоприемника обеспечивает настройку на определенную радиостанцию.
Фильтры используются в звуковой аппаратуре в многополосных эквалайзерах для корректировки АЧХ, для разделения сигналов низких, средних и высоких звуковых частот в многополосных акустических системах, в схемах частотной коррекции магнитофонов и др.
Статью про теория фильтров я написал специально для тебя. Если ты хотел бы внести свой вклад в развитие теории и практики, ты можешь написать коммент или статью отправив на мою почту в разделе контакты. Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое теория фильтров, фильры сигналов, фильтр, влияние фильтра на параметры импульса и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Устройства СВЧ и антенны
Комментарии
Оставить комментарий
Устройства СВЧ и антенны
Термины: Устройства СВЧ и антенны