Лекция
Привет, сегодня поговорим про эквивалентные автоматы, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое эквивалентные автоматы , настоятельно рекомендую прочитать все из категории Теория автоматов.
Реакцией автомата называется последовательность выходных сигналов автомата, полученная под воздействием некоторой последовательности входных сигналов, то есть реакция - это выходное слово автомата на конкретное входное слово.
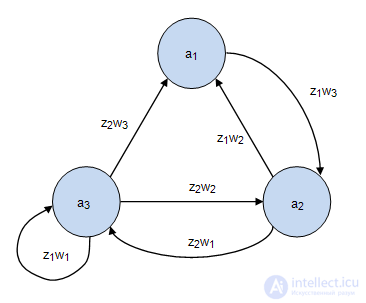
Так для автомата на рис.2.1 формирование реакции представлено в табл.2.1. На вход автомата подается последовательность входных сигналов  . Автомат в исходном состоянии находится в состоянии
. Автомат в исходном состоянии находится в состоянии  . Поступающий входнойсигнал
. Поступающий входнойсигнал 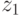 переводит автомат в состояние
переводит автомат в состояние 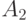 , причем на этом переходе в тот же самый дискретный момент времени формируется выходной сигнал
, причем на этом переходе в тот же самый дискретный момент времени формируется выходной сигнал 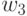 . Во второй момент времени
. Во второй момент времени 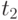 на автомат действует входной сигнал
на автомат действует входной сигнал 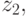 который переводитавтомат в состояние
который переводитавтомат в состояние 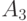 , причем на этом переходе в тот же самый дискретный момент времени
, причем на этом переходе в тот же самый дискретный момент времени 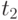 формируется выходной сигнал
формируется выходной сигнал 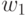 и так далее. В результате на входное слово
и так далее. В результате на входное слово  сформировано выходное слово
сформировано выходное слово  , которое и является реакцией автомата.
, которое и является реакцией автомата.
| Моменты времени t | t1 | t2 | t3 | t4 | t5 | |
|---|---|---|---|---|---|---|
| Входные сигналы | z1 | z2 | z1 | z2 | z2 | |
| Состояния | a 1 | a 2 | a3 | a 3 | a2 | a1 |
| Выходные сигналы | w3 | w1 | w1 | w2 | w2 |
Для автомата Мура формирование реакции происходит аналогично, с той лишь разницей, что в автомате Мура выходной сигнал выдается не на переходе автомата из состояния 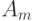 в состояние
в состояние 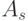 как в автомате Мили, а после того, как автомат перешел в состояние
как в автомате Мили, а после того, как автомат перешел в состояние 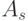 .
.
Автомат Мили  на рис.2.2 установлен в исходное состояние
на рис.2.2 установлен в исходное состояние 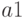 .На вход подается входное слово:
.На вход подается входное слово:  . В результате сформировано выходное слово
. В результате сформировано выходное слово  , которое является реакцией автомата (табл.2.2). Автомат Мура
, которое является реакцией автомата (табл.2.2). Автомат Мура 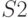 граф, которого представлен рис.2.3, установлен в исходное состояние
граф, которого представлен рис.2.3, установлен в исходное состояние 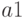 .
.
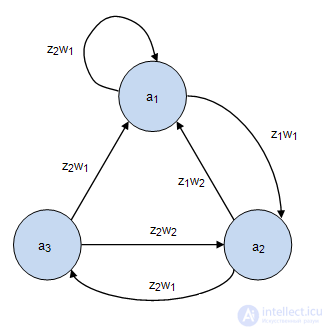
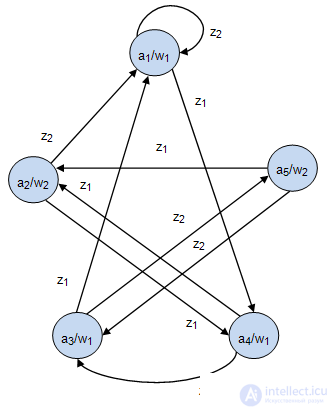
На вход подается такое же входное слово:  . Об этом говорит сайт https://intellect.icu . В результате сформировано выходное слово
. Об этом говорит сайт https://intellect.icu . В результате сформировано выходное слово  , которое является реакцией автомата (табл.2.3).
, которое является реакцией автомата (табл.2.3).
| Моменты времени | t1 | t2 | t3 | t4 | t5 | t6 | t7 |
|---|---|---|---|---|---|---|---|
| Входное слово | z1 | z1 | z2 | z1 | z2 | z2 | |
| Состояния | a1 | a2 | a1 | a1 | a2 | a3 | a2 |
| Выходнoе слово | w1 | w2 | w1 | w1 | w1 | w2 | |
| реакция автомата | |||||||
| Моменты времени | t1 | t2 | t3 | t4 | t5 | t6 | t7 |
|---|---|---|---|---|---|---|---|
| Входное слово | z1 | z1 | z2 | z1 | z2 | z2 | |
| Состояния | a1 | a4 | a2 | a1 | a4 | a3 | a5 |
| Выходнoе слово | w1 | w1 | w2 | w1 | w1 | w1 | w2 |
| реакция автомата | |||||||
Два автомата  и
и 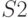 называются эквивалентными, если:
называются эквивалентными, если:
Существует теорема: для любого автомата Мура существует эквивалентный автомат Мили и наоборот.
При табличном задании таблица переходов автомата Мили совпадает с таблицей переходов автомата Мура. Таблица выходовавтомата Мили получается из таблицы переходов заменой символа 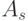 , стоящего на пересечении строки
, стоящего на пересечении строки  и столбца
и столбца 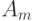 , на символ
, на символ 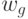 , отмечающий столбец
, отмечающий столбец 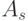 в совмещенной таблице автомата Мура.
в совмещенной таблице автомата Мура.
Пусть задан автомат Мура (табл.2.4). Таблица переходов эквивалентного автомата Мили (табл.2.5) совпадает с совмещенной таблицей автомата Мура, представляющей переходы автомата, а таблица выходов 2.6 получена следующим образом. Считается, что на переходе из состояния 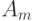 в состояние
в состояние 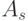 в эквивалентном автомате Мили должен быть сформирован такой же выходной сигнал, что и в автомате Мура, после того как автомат перешел в состояние
в эквивалентном автомате Мили должен быть сформирован такой же выходной сигнал, что и в автомате Мура, после того как автомат перешел в состояние  , то есть выходной сигнал
, то есть выходной сигнал 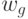 .
.
| w1 | w2 | w3 | w2 | w3 | |
|---|---|---|---|---|---|
| a1 | a2 | a3 | a4 | a5 | |
| z1 | a2 | a5 | a5 | a3 | a3 |
| z2 | a4 | a2 | a2 | a1 | a1 |
| a1 | a2 | a3 | a4 | a5 | |
|---|---|---|---|---|---|
| z1 | a2 | a5 | a5 | a3 | a3 |
| z2 | a4 | a2 | a2 | a1 | a1 |
| a1 | a2 | a3 | a4 | a5 | |
|---|---|---|---|---|---|
| z1 | w2 | w3 | w3 | w3 | w3 |
| z2 | w2 | w2 | w2 | w1 | w1 |
Рассмотрим переход автомата из состояния 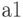 в состояние
в состояние 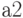 . В автомате Мура состоянию
. В автомате Мура состоянию 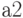 соответствует выходной сигнал
соответствует выходной сигнал 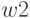 , следовательно в табл.2.6 на переходе из состояния
, следовательно в табл.2.6 на переходе из состояния 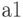 по входному сигналу
по входному сигналу 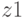 ставим
ставим 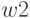 и так далее.
и так далее.
При графическом задании автомата Мура переход к автомату Мили выполняется следующим образом: выходной сигнал 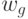 , формируемый в состоянии
, формируемый в состоянии 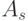 , переносится на все дуги, входящие в эту вершину, графическая интерпретация этого показана нарис.2.4, а пример трансформации автомата Мура в эквивалентный автомат Мили показан на рис.2.5.
, переносится на все дуги, входящие в эту вершину, графическая интерпретация этого показана нарис.2.4, а пример трансформации автомата Мура в эквивалентный автомат Мили показан на рис.2.5.
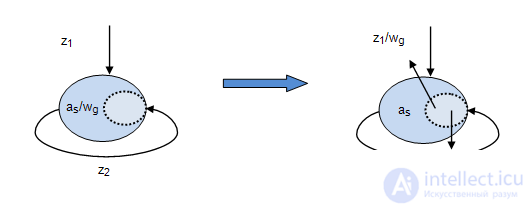
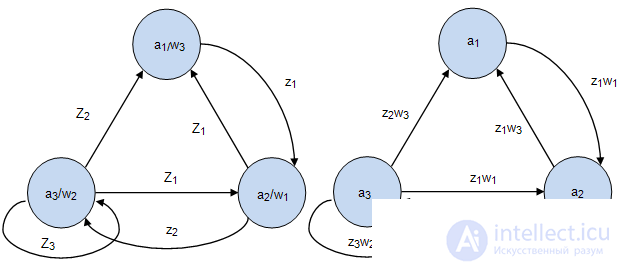
Ограничение: В автомате Мили не должно быть переходящих состояний, т.е. состояний, в которых имеется хотя бы одна выходящаядуга и не имеется ни одной входящей дуги, так как показано на рис.2.6.
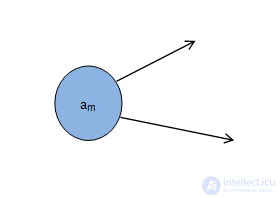
В автомате Мура выходной сигнал 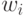 формируется как функция
формируется как функция 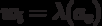 , а в автомате Мили -
, а в автомате Мили -  . Причем
. Причем 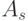 - текущее состояние автомата,
- текущее состояние автомата, 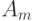 - предыдущее состояние автомата. Таким образом, состояние
- предыдущее состояние автомата. Таким образом, состояние 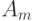 соответствует группе
соответствует группе  , число которых равно количеству различных выходных сигналов
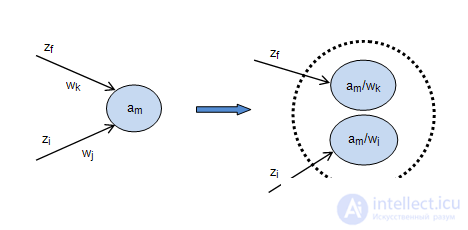
, число которых равно количеству различных выходных сигналов  , расположенных на входящих дугах. Графическая интерпретация этого показана на рис.2.7.
, расположенных на входящих дугах. Графическая интерпретация этого показана на рис.2.7.
Пусть дан автомат Мили:  . Требуется перейти к эквивалентному автомату Мура
. Требуется перейти к эквивалентному автомату Мура 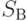 , то есть требуется построить такой автомат Мура :
, то есть требуется построить такой автомат Мура :  , что
, что  и
и . Рассмотрим пример. Дан автомат Мили рис.2.8-2.9. Построим множество состояний автомата
. Рассмотрим пример. Дан автомат Мили рис.2.8-2.9. Построим множество состояний автомата 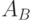 . Для этого находим пары:
. Для этого находим пары:
 ;
;
 ;
;
 ;
;
 .
.
Переобозначив  соответственно как
соответственно как 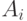 , получим граф, изображенный на рис.2.8-2.9.
, получим граф, изображенный на рис.2.8-2.9.
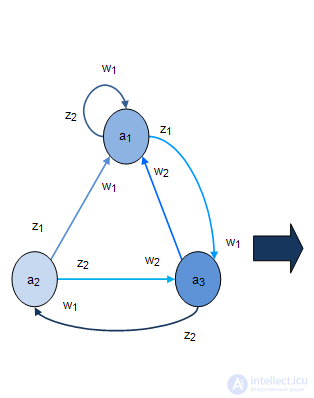 Рис. 2.8. |
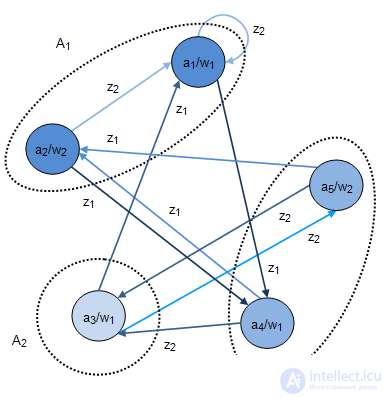 Рис. 2.8. |
Надеюсь, эта статья про эквивалентные автоматы, была вам полезна, счастья и удачи в ваших начинаниях! Надеюсь, что теперь ты понял что такое эквивалентные автоматы и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория автоматов
Из статьи мы узнали кратко, но содержательно про эквивалентные автоматы
Комментарии
Оставить комментарий
Теория цифровых автоматов
Термины: Теория цифровых автоматов