1. Нареч.
2. Соотносится по значение с прилагательное : случайный (1,2).
3. разговорное Употребляется как вводное слово; соответствует по значению сл: кстати, между прочим.
1. Нареч. 1. Нареч. к случайный в 1 и 2 значение Случайно встретиться с кем кто-нибудь Случайно купить что кто-нибудь - Да вместе вы зачем? Нельзя, чтобы случайно. Грибоедов. Мы случайно сведены судьбою. Лермонтов. Мы встречались случайно. Я его случайно знаю. 2. в значение вводного слова. Между прочим, кстати сказать ( просторечие фамильярное ). У вас, случайно, нет ли папирос? Вы, случайно, не на собрание идете? Не случайно - не без причины, не без оснований, с умыслом. Не случайно физкультуре уделяется у нас большое внимание.
Нареч. к случайный (в 1 значение ).
Случайно вас когда-то встретя, В вас искру нежности заметя, Я ей поверить не посмел. Пушкин, Евгений Онегин.
Дом Толстого был домом простым, со сборной мебелью и с потемневшими зеркалами, случайно оставшимися от отцовского дома. Шкловский, Лев Толстой.
в значение вводное слово (обычно в отрицательном предложении: случайно, не…). Разг.
Кстати, между прочим.
{Мать Валентины} спросила мальчика: — А папа твой, случайно, родом не из Одессы? — Из Одессы. Катаев, За власть Советов.
... . предельную теорему и теорему о больших уклонениях Как цепь Маркова Одномерное дискретное случайное блуждание является цепью Маркова с целыми состояниями ., чье начальное распределение задается функцией ... ... функции , что применяется при решении задач оптимизации . При использовании специального закона распределения случайных величин может быть получена . модификация метода случайных блужданий , именуемая полетами ... (вероятностные процессы)
... , меняет свои состояния только в моменты времени ,.число которых конечно или счетно Случайный процесс называется процессом с непрерывным временем , если переход из. состояния в состояние может происходить ... ... называется траекторией или реализацией случайной функции . Примеры , где называется стандартной гауссовской (нормальной ) случайной последовательностью Пусть , и - случайная величина Тогда является случайным процессом Функция X(t) называется случайной ... (вероятностные процессы)
... . пространстве X на пространстве элементарных событий называется интеграл ( в предположении , что функция является интегрируемой ). Дисперсией случайной величины называется величина , равная :. В статистике для дисперсии часто употребляется обозначение или. Величина ... ... в том, что с ее . помощью удается достичь единообразного математического описания дискретных , непрерывных и дискретно-непрерывных .случайных величин Тем не менее , существуют разные случайные величины , имеющие одинаковые ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
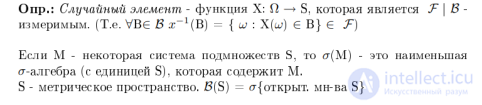... термины Если , то параметр может интерпретироваться как время Тогда случайная функция называется случайным процессом Если множество дискретно , например , то такой случайный процесс называется случайной ... ... называется процессом с непрерывными состояниями , если значением случайного . процесса является непрерывная случайная величина Случайный процесс называется случайным процессом с дискретными состояниями , если значением . случайного процесса является дискретная ... (вероятностные процессы)
... преобразования демонстрируется на рис Рис Схема перевода числа из интервала (0; в интервал (a; b.) Теперь x — случайное число , равномерно распределенное в диапазоне от a. до b За эталон генератора случайных чисел (ГСЧ ... ... упала решкой , то запишите «0», если орлом , то «1 ». Итак , допустим , что в результате эксперимента получили случайную последовательность Начертите интервал от 0 до Считывая числа в последовательности слева . направо , разбивайте интервал ... (Моделирование и Моделирование систем)
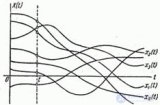... .цели ; отклонение траектории управляемого снаряда от теоретической в процессе управления или. самонаведения Такие случайные величины , изменяющиеся в процессе опыта , мы будем в. отличие от обычных случайных величин ... ... аргументов : трех координат .и времени В данном курсе мы будем рассматривать только случайные функции одного . аргумента Так как этим аргументом чаще всего является время , будем ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
Комментарии
Оставить комментарий