Тоже самое что слово - разбросной,
1. А) Служащий для разбрасывания чего -либо б) Производящий разбрасывание.
2. Осуществляемый путем разбрасывания, рассеивания.
1. Разбросная, разбросное (сельское хозяйство). прилагательное , по значение связанное с разброской чего кто-нибудь (семян, удобрений) на поверхность почвы. Разбросной посев.
сельское хозяйство
Связанный с разброской, разбрасыванием чего -либо (семян, удобрений) по поверхности почвы.
Разбросной сев.
Предназначенный, служащий для разброски.
Разбросная сеялка.

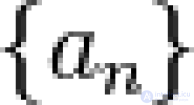 ... скалярами и где является многочленом . от для всех В общем , произведения Адамара рациональных функций порождают рациональные производящие функции . Аналогично , если- двумерная рациональная производящая функция , то соответствующая ей диагональная . производящая ... ... соотношении Например , рассмотрим числа Фибоначчи . Найдите рекуррентные соотношения для последовательностей - вид производящей функции может предлагать . формулу рекуррентности Найдите взаимосвязи между последовательностями - если производящие функции ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... скалярами и где является многочленом . от для всех В общем , произведения Адамара рациональных функций порождают рациональные производящие функции . Аналогично , если- двумерная рациональная производящая функция , то соответствующая ей диагональная . производящая ... ... соотношении Например , рассмотрим числа Фибоначчи . Найдите рекуррентные соотношения для последовательностей - вид производящей функции может предлагать . формулу рекуррентности Найдите взаимосвязи между последовательностями - если производящие функции ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
 ... (при этом каждый член в композиции можно трактовать как количество . элементов i в выборке ). При фиксированном m производящей функцией последовательности является:. Поэтому число может быть найдено как коэффициент при в разложении . по степеням ... ... дискретной ), имеющая распределение . вероятностей то ее математическое ожидание может быть выражено через производящую функцию . последовательности как значение первой производной в единице : (стоит отметить , что ряд . для P(s) сходится ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... (при этом каждый член в композиции можно трактовать как количество . элементов i в выборке ). При фиксированном m производящей функцией последовательности является:. Поэтому число может быть найдено как коэффициент при в разложении . по степеням ... ... дискретной ), имеющая распределение . вероятностей то ее математическое ожидание может быть выражено через производящую функцию . последовательности как значение первой производной в единице : (стоит отметить , что ряд . для P(s) сходится ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
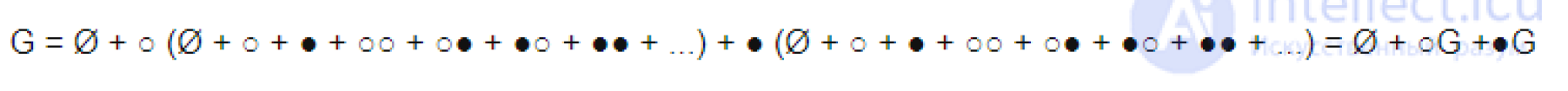 ... быть любой объект , для которого определены операции сложения .и умножения История возникновения производящих функций Известно , что начало методу производящих функций положил английский математик Абрахам ... ... способами При решении этой задачи он использовал никому неизвестный на то. время метод производящих функций , которому и посвящена данная статья К этой задаче мы вернемся немного ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... быть любой объект , для которого определены операции сложения .и умножения История возникновения производящих функций Известно , что начало методу производящих функций положил английский математик Абрахам ... ... способами При решении этой задачи он использовал никому неизвестный на то. время метод производящих функций , которому и посвящена данная статья К этой задаче мы вернемся немного ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
 ... биномиальный ряд (см . «Расширенные биномиальные коэффициенты »;):. Совершенно аналогично нужно поступить с производящей функцией последовательностей №10 и. №11 : если теперь заменить m на m+1 и использовать тот . факт ... ... . факт , что для целых положительных тождество , то получим одиннадцатую .строку таблицы : Последовательность №9 и производящая функция для нее следуют из биномиальной . теоремы (после замены a на z, а b на 1 ),.утверждение которой доказывается ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... биномиальный ряд (см . «Расширенные биномиальные коэффициенты »;):. Совершенно аналогично нужно поступить с производящей функцией последовательностей №10 и. №11 : если теперь заменить m на m+1 и использовать тот . факт ... ... . факт , что для целых положительных тождество , то получим одиннадцатую .строку таблицы : Последовательность №9 и производящая функция для нее следуют из биномиальной . теоремы (после замены a на z, а b на 1 ),.утверждение которой доказывается ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
 ... две случайные величины , и. Тогда В частности , если обе величины абсолютно непрерывны , то совпадение производящих . функций моментов влечет совпадение плотностей Если обе случайные величины дискретны ... ... моментов влечет совпадение плотностей Если обе случайные величины дискретны , то совпадение производящих функций моментов . влечет совпадение функций вероятности Производящая функция моментов как функция ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... две случайные величины , и. Тогда В частности , если обе величины абсолютно непрерывны , то совпадение производящих . функций моментов влечет совпадение плотностей Если обе случайные величины дискретны ... ... моментов влечет совпадение плотностей Если обе случайные величины дискретны , то совпадение производящих функций моментов . влечет совпадение функций вероятности Производящая функция моментов как функция ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
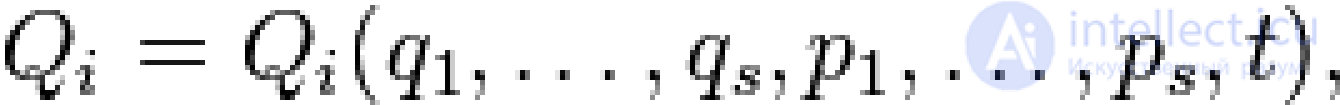 ... дифференциал некоторой функции . (предполагается , что и также выражены через старые переменные ). Она называется производящей функцией канонического преобразования Канонические преобразования взаимнооднозначно определяются производящей функцией и валентностью ... ... , а также для гамильтониана только на.константу , то часто рассматривают только унивалентные канонические преобразования Производящая функция часто может быть выражена не через старые координаты . и импульсы , а через любые ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
... дифференциал некоторой функции . (предполагается , что и также выражены через старые переменные ). Она называется производящей функцией канонического преобразования Канонические преобразования взаимнооднозначно определяются производящей функцией и валентностью ... ... , а также для гамильтониана только на.константу , то часто рассматривают только унивалентные канонические преобразования Производящая функция часто может быть выражена не через старые координаты . и импульсы , а через любые ... (Теория вероятностей. Математическая статистика и Стохастический анализ )
Комментарии
Оставить комментарий