1. Нареч. В виде полуколец.

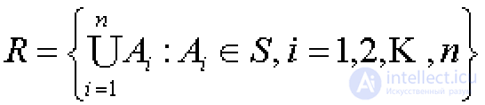 ... . Доказать что является алгеброй Доказать , что система всех интервалов , отрезков и полуинтервалов из отрезка . образует полукольцо Доказать , что система всех интервалов (включая пустой ) и система всех . отрезков (с добавлением ... ... интервалов (включая пустой ) и система всех . отрезков (с добавлением пустого множества ) в R не является полукольцом Доказать , что система всех открытых множеств в R не является. полукольцом Пусть - полукольцо (кольцо ... (Функциональный анализ)
... . Доказать что является алгеброй Доказать , что система всех интервалов , отрезков и полуинтервалов из отрезка . образует полукольцо Доказать , что система всех интервалов (включая пустой ) и система всех . отрезков (с добавлением ... ... интервалов (включая пустой ) и система всех . отрезков (с добавлением пустого множества ) в R не является полукольцом Доказать , что система всех открытых множеств в R не является. полукольцом Пусть - полукольцо (кольцо ... (Функциональный анализ)
 ... из всех . точек х, координаты которых удовлетворяют неравенствам £ xi < bi , где.i = 1 , , n Пусть и - полукольца на множествах и., соответственно Построим систему множеств P = ´, т е А´В ÎP тогда и только тогда , когда и. Лемма ... ... и., соответственно Построим систему множеств P = ´, т е А´В ÎP тогда и только тогда , когда и. Лемма Система P является полукольцом в ´Х. Доказательство Æ = Æ´ÆÎP Если ´, ´, то ´ Ç.´ = ( ´( Î P (в силу свойств полуколец .и P Пусть ´, ´ и ´ Ì.´, последнее влечет вложения множеств ... (Функциональный анализ)
... из всех . точек х, координаты которых удовлетворяют неравенствам £ xi < bi , где.i = 1 , , n Пусть и - полукольца на множествах и., соответственно Построим систему множеств P = ´, т е А´В ÎP тогда и только тогда , когда и. Лемма ... ... и., соответственно Построим систему множеств P = ´, т е А´В ÎP тогда и только тогда , когда и. Лемма Система P является полукольцом в ´Х. Доказательство Æ = Æ´ÆÎP Если ´, ´, то ´ Ç.´ = ( ´( Î P (в силу свойств полуколец .и P Пусть ´, ´ и ´ Ì.´, последнее влечет вложения множеств ... (Функциональный анализ)
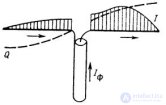 ... и приближенно равно входному сопротивлению завороченной двухпроводной .линии длиной , равной длине полукольца Это реактивное сопротивление сильно изменяется при изменении частоты Если длина полукольца ... (Устройства СВЧ и антенны)
... и приближенно равно входному сопротивлению завороченной двухпроводной .линии длиной , равной длине полукольца Это реактивное сопротивление сильно изменяется при изменении частоты Если длина полукольца ... (Устройства СВЧ и антенны)
 ... ÎP и А Ì , то m(A.) £ (полуаддитивность меры ) Доказательство Легко вытекает из свойства аддитивности и неотрицательности , так как m.(Æ) = m(ÆÈÆ) = m(Æ) + m(Æ) = (Æ). В силу свойств полукольца найдется конечный набор множеств ÎP. таких , что В = А + Тогда из аддитивности m вытекает m(B) = m(A) + m.(), откуда и неотрицательности ... ... из них обязательно попадает полностью ). Отсюда уже легко следует , что m(А) = Теорема Функция V, заданная на полукольце P ячеек в Rn . и равная для каждой ячейки ее объему - мера в.Rn Доказательство Практически ... (Функциональный анализ)
... ÎP и А Ì , то m(A.) £ (полуаддитивность меры ) Доказательство Легко вытекает из свойства аддитивности и неотрицательности , так как m.(Æ) = m(ÆÈÆ) = m(Æ) + m(Æ) = (Æ). В силу свойств полукольца найдется конечный набор множеств ÎP. таких , что В = А + Тогда из аддитивности m вытекает m(B) = m(A) + m.(), откуда и неотрицательности ... ... из них обязательно попадает полностью ). Отсюда уже легко следует , что m(А) = Теорема Функция V, заданная на полукольце P ячеек в Rn . и равная для каждой ячейки ее объему - мера в.Rn Доказательство Практически ... (Функциональный анализ)
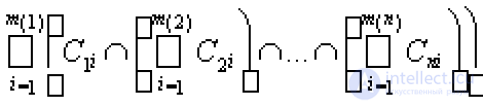 ... очевидно Пусть m*(En ) < +¥ для всех n Тогда для произвольного e > 0 найдутся покрытие Ì Bkn . множествами из полукольца P такие, что m*() ³ Так как Е Ì En , а Ì Bkn , то. Е Ì Bkn Следовательно m*(Е) £ m(Bkn ) £ (m*(En ) + e/) = m*(En .) + e В силу произвольности ... ... функция , определенная для - Е Ì X.по следующему правилу : Если для Е существует не более чем счетное покрытие из. полукольца P, т е Е Ì , где Î P (n = 1 , 2 ., ), то m*(Е) = inf { m(An )}, где нижняя грань берется . по всевозможным покрытиям указанного ... (Функциональный анализ)
... очевидно Пусть m*(En ) < +¥ для всех n Тогда для произвольного e > 0 найдутся покрытие Ì Bkn . множествами из полукольца P такие, что m*() ³ Так как Е Ì En , а Ì Bkn , то. Е Ì Bkn Следовательно m*(Е) £ m(Bkn ) £ (m*(En ) + e/) = m*(En .) + e В силу произвольности ... ... функция , определенная для - Е Ì X.по следующему правилу : Если для Е существует не более чем счетное покрытие из. полукольца P, т е Е Ì , где Î P (n = 1 , 2 ., ), то m*(Е) = inf { m(An )}, где нижняя грань берется . по всевозможным покрытиям указанного ... (Функциональный анализ)
 ... в этой теореме ., порождена внешней мерой m*. Теорема 10 Пусть m - мера в X, заданная на полукольце . P, m* - внешняя мера , порожденная мерой m, m - мера , порожденная .внешней мерой m*, тогда m - продолжение ... ... множество будем называть так же измеримым Теорема Пусть m - стандартное продолжение на S меры m. с полукольца P в X Если В Ì X и для - e > 0 $ A ÎS.: В ÌA и M(А) < e, то В ÎS и.m(В) = Доказательство В силу стандартности продолжения m найдется покрытие А (а значит . и В) множествами из полукольца ... (Функциональный анализ)
... в этой теореме ., порождена внешней мерой m*. Теорема 10 Пусть m - мера в X, заданная на полукольце . P, m* - внешняя мера , порожденная мерой m, m - мера , порожденная .внешней мерой m*, тогда m - продолжение ... ... множество будем называть так же измеримым Теорема Пусть m - стандартное продолжение на S меры m. с полукольца P в X Если В Ì X и для - e > 0 $ A ÎS.: В ÌA и M(А) < e, то В ÎS и.m(В) = Доказательство В силу стандартности продолжения m найдется покрытие А (а значит . и В) множествами из полукольца ... (Функциональный анализ)
Комментарии
Оставить комментарий