1. Приносящий пользу ( противоположное или противоположность : вредный).2. а) Пригодный для данной цели. б) Составляющий ту часть целого, которая используется по определенному назначению.
1. Приносящий пользу. Полезное насекомое. Полезная книга. Полезная деятельность. Молоко пить полезно ( в значении сказуемого ). 2. полная форма прилагательного ф. Пригодный для определенной цели, иду- щий в дело. Полезная жилая площадь. По- лезные ископаемые (используемые в про-1 изводстве).
1. Полезная, полезное; полезен, полезна, полезно. 1. Приносящий пользу, противоположное или противоположность вредный. Полезный человек. Полезное растение. А кто полезен вам, к тому вы нерадивы. Крылов. Здоровью моему полезен русский холод. Пушкин. Не всё хлопотать о полезном; позаботимся и о приятном. Писемский. Сочетать полезное с приятным. Полезная деятельность.
2. Содействующий здоровью, поддерживающий силы и бодрость. Прогулка полезна. Гулять очень полезно. Полезная пища. 2. Пригодный, нужный для какой кто-нибудь определенной цели; составляющий ту часть целого, к-края может быть использована по непосредственному назначению ( специальное ). Полезная жилая площадь. Коэффициент полезного действия. Полезный объем помещений.
-ая, -ое; -зен, -зна, -зно.
1.
Приносящий пользу, способный приносить пользу.
Полезные начинания. Полезная книга. Полезная пища. Прогулки полезны.
Долг требовал, чтобы я явился туда, где служба моя могла еще быть полезна отечеству. Пушкин, Капитанская дочка.
— Хотелось непременно что-то делать, быть нужной, полезной. Игишев, Шахтеры.
2.
только полная форма прилагательного ф. Спец. Составляющий ту часть целого, которая может быть использована по непосредственному назначению.
Полезная площадь. Коэффициент полезного действия. Полезное сопротивление. Полезный тоннаж.
- полезные ископаемые- чем могу быть полезен?
... которой представляет комбинацию двух . товаров , которые имеют для потребления одинаковую общую полезность Подходы к исследованию функции полезности Ординалистский и Кардиналистский Кардиналистский - Предполагает точное количественное ... ... оценивает и сравнивает не отдельные единицы благ , а. наборы (потребительские корзины ) Оптимизация полезности с точки зрения экономической теории Второй закон Госсена : чтобы получить максимум ... (Теория принятия решений)
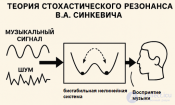... : музыкальные : музыкальные ислуховые ислуховые стимулы стимулы могут могут переключать переключать систему систему между.двумя между.двумя устойчивыми устойчивыми состояниями состояниями Шум Шум какполезный какполезный фактор фактор : приопределенной : приопределенной интенсивности интенсивности шум шум усиливает усиливает слабые слабые .сигналы .сигналы , делая , делая ихдоступными ихдоступными длявосприятия длявосприятия ... (Музыкальная психология)
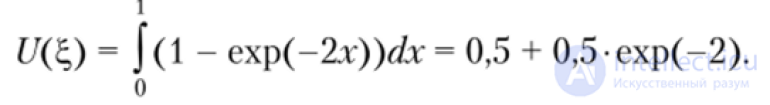... Иногда на функцию и накладывают более жесткие ограничения , например , свойство . вогнутости Функция полезности порождает отношения предпочтения на множестве функций распределения . следующим образом т е случайная величина ... ... образом т е случайная величина , не менее предпочтительна , чем в том и только в том. случае, если {/( ) > Щс ) Пример функции полезности Рассмотрим функцию и(. ) = 1 - ехр (-2 ), > Тогда для случайной величины 2 ;, имеющей ... (Теория принятия решений)
... можно записать следующее соотношение Следовательно , необходимым условием существования аддитивной функции полезности является условие соответственных . замещений где Хв , Ха Хп - ЛКЗ в точках В, С и. О соответственно Можно ... ... Можно доказать , что это условие является достаточным Процедура построения кривых безразличия в случае аддитивной функции полезности вида . проще , чем в общем случае Как уже упоминалось в параграфе 4 , функция полезности ... (Теория принятия решений)
... максимум h имеет. место при (рис Из кривой видно , что трансформатор имеет практически постоянный коэффициент полезного . действия в широком диапазоне изменения нагрузки от 0,5 до.1 , При малых нагрузках ... (Источники питания радиоэлектронной аппаратуры)
... егоаттестации ирегистрации ., атакже правомочия наведение дел , связанных справовой охраной .изобретений , полезных моделей ипромышленных образцов , определяются Правительством Российской Федерации Заявление овыдаче патента ... (Авторское право)
Комментарии
Оставить комментарий