1. Соотносящийся по значение с существительное : камбий, связанный с ним.
2. Свойственный камбию, характерный для него.
Бот.
прилагательное к камбий.
Камбиальный слой. Камбиальные клетки.

 ... , тохорошо . определена , и формула возведения в степень упрощается до формулы де .Муавра : П п й корни из комплексного числа г задается для 0 ≤ k ≤ n - 1 . (Вотявляется обычным (положительным ) корнем n- й степени из положительного действительного ... ... , как правило , опускаем : Сложение ассоциативно :. : Существует элемент 0 (ноль ) такой , что. : Для всякого комплексного числа существует «противоположный ему »; элемент . : Для всяких комплексных чисел определено ... (Алгебра)
... , тохорошо . определена , и формула возведения в степень упрощается до формулы де .Муавра : П п й корни из комплексного числа г задается для 0 ≤ k ≤ n - 1 . (Вотявляется обычным (положительным ) корнем n- й степени из положительного действительного ... ... , как правило , опускаем : Сложение ассоциативно :. : Существует элемент 0 (ноль ) такой , что. : Для всякого комплексного числа существует «противоположный ему »; элемент . : Для всяких комплексных чисел определено ... (Алгебра)
 ... в. моделях теории струн Примерами многообразий Калаби-Яу являются эллиптические кривые , поверхности и комплексные . абелевы многообразия комплексные разновидности Фано . Комплексное многообразие Фано - это комплексное алгебраическое ... ... задаваться нулевым . набором конечного числа однородных многочленов . Чтобы определить общее комплексное алгебраическое или комплексно аналитическое многообразие , необходимо . понятие локально окольцованного пространства . Комплексная ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))
... в. моделях теории струн Примерами многообразий Калаби-Яу являются эллиптические кривые , поверхности и комплексные . абелевы многообразия комплексные разновидности Фано . Комплексное многообразие Фано - это комплексное алгебраическое ... ... задаваться нулевым . набором конечного числа однородных многочленов . Чтобы определить общее комплексное алгебраическое или комплексно аналитическое многообразие , необходимо . понятие локально окольцованного пространства . Комплексная ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))
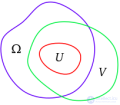 ... сходится равномерно в. Таким образом , можно получить аналогичный радиус сходимости для одной комплексной . переменной , но есть точка , в которой она сходится за пределами .круга сходимости Теорема идентичности Когда ... ... Штейна -.это комплексная поверхность X с вещественной функцией Морса f на X., такая, что вдали от критических точек f поверхность поле комплексных .касаний к прообразуявляется контактной структурой , которая индуцирует ориентацию на X c., совпадающую с обычной ориентацией ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))
... сходится равномерно в. Таким образом , можно получить аналогичный радиус сходимости для одной комплексной . переменной , но есть точка , в которой она сходится за пределами .круга сходимости Теорема идентичности Когда ... ... Штейна -.это комплексная поверхность X с вещественной функцией Морса f на X., такая, что вдали от критических точек f поверхность поле комплексных .касаний к прообразуявляется контактной структурой , которая индуцирует ориентацию на X c., совпадающую с обычной ориентацией ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))
 ... от нуля , то наз существенно особой точкой Существенно особые точки характеризуются тем, что для любого комплексного числа . а существует последовательность , сходящаяся к при , такая, что. Пусть замкнутый контур , лежащий в области аналитичности ... ... теорема и. др ) Понятие аналитичности имеет смысл также и на множествах более сложных ., чем области комплексной плоскости С, но локально устроенных как последние Напр , добавляя к С бесконечно удаленную точку , получают ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))
... от нуля , то наз существенно особой точкой Существенно особые точки характеризуются тем, что для любого комплексного числа . а существует последовательность , сходящаяся к при , такая, что. Пусть замкнутый контур , лежащий в области аналитичности ... ... теорема и. др ) Понятие аналитичности имеет смысл также и на множествах более сложных ., чем области комплексной плоскости С, но локально устроенных как последние Напр , добавляя к С бесконечно удаленную точку , получают ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))
 ... й степени Интегральная теорема Коши Интегральная теорема Коши - утверждение из теории функций комплексного переменного Для любой функции , аналитической в некоторой односвязной области и для. любой замкнутой ... ... , которые образуют вещественную .группу Ли Вариации и обобщения Если вместо области на комплексной плоскости рассматривать область на произвольной . римановой поверхности , то мы приходим к теореме об униформизации ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))
... й степени Интегральная теорема Коши Интегральная теорема Коши - утверждение из теории функций комплексного переменного Для любой функции , аналитической в некоторой односвязной области и для. любой замкнутой ... ... , которые образуют вещественную .группу Ли Вариации и обобщения Если вместо области на комплексной плоскости рассматривать область на произвольной . римановой поверхности , то мы приходим к теореме об униформизации ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))
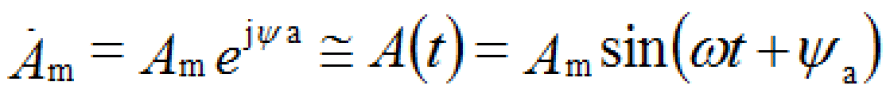 ... разбивается на четыре четверти :Итак , рассмотрим нашу тригонометрическую . функцию A(t) представленную в виде комплексной величины на комплексной .плоскости Получается , что наша функция представлена в виде вектора вращающегося ... ... прибавить 180 ° или π Если = 0, то комплексное число называется мнимым , аргумент ψа. = ± 90 ° Если = 0, то комплексное число называется действительным , ψа =.0, ± πПростейшие математические операции с комплексными числамиПростейшие математические операции такие, как. сложение ... (Электротехника, Схемотехника, Аналоговые устройства)
... разбивается на четыре четверти :Итак , рассмотрим нашу тригонометрическую . функцию A(t) представленную в виде комплексной величины на комплексной .плоскости Получается , что наша функция представлена в виде вектора вращающегося ... ... прибавить 180 ° или π Если = 0, то комплексное число называется мнимым , аргумент ψа. = ± 90 ° Если = 0, то комплексное число называется действительным , ψа =.0, ± πПростейшие математические операции с комплексными числамиПростейшие математические операции такие, как. сложение ... (Электротехника, Схемотехника, Аналоговые устройства)
Комментарии
Оставить комментарий