1. прилагательное Поддающийся измерению.
1. Измеримая, измеримое; измерим, измерима, измеримо ( книжное ). Такой, что можно измерить. Измеримая величина.
-ая, -ое; -рим, -а, -о. Такой, что можно измерить, поддающийся измерению (в 1 значение ).
Измеримая величина.

 ... Следующая теорема Лузина устанавливает связь между свойствами измеримости и непрерывности . функций Рассмотрим измеримое пространство (R, S, m) меры Лебега на прямой . R Определение Говорят , что функция f: Е ® R обладает С-свойством на. множестве ... ... , , а функция f. 3 (x) измерима на А Доказать , что f (x) также измерима на А Построить такую функцию f (x) на [0, , что f 2 .(x) измерима относительно меры Лебега на [0, , но f (x).неизмерима относительно этой меры Построить непрерывную неубывающую ... (Функциональный анализ)
... Следующая теорема Лузина устанавливает связь между свойствами измеримости и непрерывности . функций Рассмотрим измеримое пространство (R, S, m) меры Лебега на прямой . R Определение Говорят , что функция f: Е ® R обладает С-свойством на. множестве ... ... , , а функция f. 3 (x) измерима на А Доказать , что f (x) также измерима на А Построить такую функцию f (x) на [0, , что f 2 .(x) измерима относительно меры Лебега на [0, , но f (x).неизмерима относительно этой меры Построить непрерывную неубывающую ... (Функциональный анализ)
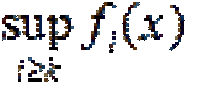 ... промежутки на прямой (отрезки , интервалы и. полуинтервалы ) являются борелевскими множествами Теорема Функция f: Е® R измерима тогда и только тогда ., когда прообраз любого борелевского множества является измеримым , т е имеет место ... ... f и g измеримы на Е Тогда их сумма f + g и произведение fg измеримы на. Е Частное f/g измеримо , если g(x) ¹ 0 при. всех х Î Е Степень |f|p измерима при всех р >. Утверждение легко вытекает из леммы и непрерывности соответствующих функций u. + v, uv и т д Следствие ... (Функциональный анализ)
... промежутки на прямой (отрезки , интервалы и. полуинтервалы ) являются борелевскими множествами Теорема Функция f: Е® R измерима тогда и только тогда ., когда прообраз любого борелевского множества является измеримым , т е имеет место ... ... f и g измеримы на Е Тогда их сумма f + g и произведение fg измеримы на. Е Частное f/g измеримо , если g(x) ¹ 0 при. всех х Î Е Степень |f|p измерима при всех р >. Утверждение легко вытекает из леммы и непрерывности соответствующих функций u. + v, uv и т д Следствие ... (Функциональный анализ)
 ... равенство :. m*(А) = m*(АÇВ) + m*(АÇВС) = m*(В) + m*(С.) Последнее равенство вытекает из простых множественных равенств : АÇВ = В, АÇВС. = С Теорема Система S всех m* измеримых множеств в X - Доказательство Пусть А = , где Î S Нам необходимо показать , что , т е выполняется равенство m*Е = m*(ЕÇА) + m*(ЕÇАС) для любого . Е Ì Х Построим ... ... теперь счетной полуаддивностью внешней меры :. ³ = m*(ЕÇА). Тогда m*(Е) ³ m*(ЕÇА) + m*(), что с. учетом замечания , сделанного после определения измеримого множества , доказывает измеримость А Теорема Функция m - мера на S Доказательство Пусть А, ÎS и А =. В силу доказанной ... (Функциональный анализ)
... равенство :. m*(А) = m*(АÇВ) + m*(АÇВС) = m*(В) + m*(С.) Последнее равенство вытекает из простых множественных равенств : АÇВ = В, АÇВС. = С Теорема Система S всех m* измеримых множеств в X - Доказательство Пусть А = , где Î S Нам необходимо показать , что , т е выполняется равенство m*Е = m*(ЕÇА) + m*(ЕÇАС) для любого . Е Ì Х Построим ... ... теперь счетной полуаддивностью внешней меры :. ³ = m*(ЕÇА). Тогда m*(Е) ³ m*(ЕÇА) + m*(), что с. учетом замечания , сделанного после определения измеримого множества , доказывает измеримость А Теорема Функция m - мера на S Доказательство Пусть А, ÎS и А =. В силу доказанной ... (Функциональный анализ)
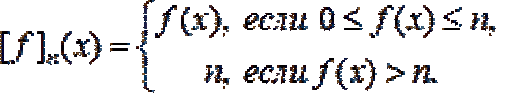 ... h - некоторая простая функция , принимающая значения , , … , yn ., yi ¹ yj при i j, и пусть E - некоторое .измеримое подмножество X Лемма 3 Интеграл от простой неотрицательной измеримой функции h(x) вычисляется по. формуле ... ... этого введем понятие положительной и отрицательной составляющих функций :. Введенные функции являются измеримыми Достаточно очевидны представления f (x) = f +(x) + f -(x), |f. (x)| = f +(x) - f -(x). Определение 3 Интегралом Лебега от измеримой функции f (x) на множестве ... (Функциональный анализ)
... h - некоторая простая функция , принимающая значения , , … , yn ., yi ¹ yj при i j, и пусть E - некоторое .измеримое подмножество X Лемма 3 Интеграл от простой неотрицательной измеримой функции h(x) вычисляется по. формуле ... ... этого введем понятие положительной и отрицательной составляющих функций :. Введенные функции являются измеримыми Достаточно очевидны представления f (x) = f +(x) + f -(x), |f. (x)| = f +(x) - f -(x). Определение 3 Интегралом Лебега от измеримой функции f (x) на множестве ... (Функциональный анализ)
 ... ряд свойств интеграла от ограниченной . измеримой функции Теорема 3 (о среднем ). Если измеримая функция f(x) на измеримом множестве Е удовлетворяет . неравенствам a £ f(x) £ b, то a×m (E) £ £ b×.m (E) Доказательство Если мы положим A = a, B = b в определении ... ... , что ® 0 Но это и означает , что = Из этой теоремы вытекает ряд следствий Следствие Если измеримые ограниченные функции f(x) и g(x.), заданные на множестве Е, эквивалентны между собой , то =. Действительно , если H = Е(f ¹ g), G = E(f. = g), то m(H) = 0 и = =. На множестве же ... (Функциональный анализ)
... ряд свойств интеграла от ограниченной . измеримой функции Теорема 3 (о среднем ). Если измеримая функция f(x) на измеримом множестве Е удовлетворяет . неравенствам a £ f(x) £ b, то a×m (E) £ £ b×.m (E) Доказательство Если мы положим A = a, B = b в определении ... ... , что ® 0 Но это и означает , что = Из этой теоремы вытекает ряд следствий Следствие Если измеримые ограниченные функции f(x) и g(x.), заданные на множестве Е, эквивалентны между собой , то =. Действительно , если H = Е(f ¹ g), G = E(f. = g), то m(H) = 0 и = =. На множестве же ... (Функциональный анализ)
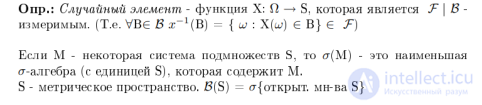 ... Случайные элементы и их распределения Случайный процесс как семейство случайных элементов и как одно измеримое . отображение Случайный процесс (вероятностный процесс , случайная функция , стохастический процесс ) в теории ... ... некоторым параметром , чаще всего играющим .роль времени или координаты Определение Пусть - измеримое пространство , множество значений параметра . Функция параметра , значениями которой являются случайные ... (вероятностные процессы)
... Случайные элементы и их распределения Случайный процесс как семейство случайных элементов и как одно измеримое . отображение Случайный процесс (вероятностный процесс , случайная функция , стохастический процесс ) в теории ... ... некоторым параметром , чаще всего играющим .роль времени или координаты Определение Пусть - измеримое пространство , множество значений параметра . Функция параметра , значениями которой являются случайные ... (вероятностные процессы)
Комментарии
Оставить комментарий