Выпуклость - понятие и значение

Рассмотрим что означает понятие и значение слова выпуклость (информация предоставлена intellect.icu).

1. Отвлеч. существительное по значение прилагательное : выпуклый ( противоположное или противоположность : вогнутость).2. Выпуклое, выдавшееся место на чем -либо

1. смотри выпуклый. 2. Выпуклое место на чем кто-нибудь В. на стене.

1. Выпуклости, 1. только единственное число Отвлеч. существительное к выпуклый. Большая выпуклость стекла. 2. Выпуклое место, возвышение. Выпуклости на стекле. 3. переносное значение, только единственное число Яркость, отчетливость. В этом поступке с особой выпуклостью выразились черты его характера. Автор с выпуклостью изобразил крестьянские типы.

-и, женский род

1.

Свойство по значение прилагательное выпуклый.

Выпуклость поверхности. Выпуклость изображения.

2.

Выпуклое, выдавшееся место на чем -либо ; выпуклина.

— Куда лезешь, --- — ворчал один угрюмый, высокий арестант --- с какими-то странными выпуклостями на своем бритом черепе. Достоевский, Записки из мертвого дома.

Стенки туннеля надо было обработать так, чтобы получилась совершенно зеркальная поверхность. Любой зазор, любая выпуклость могли вызвать завихрение воды. Паустовский, Рождение моря.

Часть речи

Имя существительное

Словоформы

выпуклости, выпуклостью, выпуклостей, выпуклостям, выпуклостями, выпуклостях

Синонимы

бампи, гаструла, горбик, вздутие, бугор, четкость, отчетливость, ясность, пастозность, стереоскопичность, резкость, чеканность, отчетистость, выпяченность, выступ, округлость, горб, живописность, яркость, живость, шишка, вогнутость, бугорок, выпуклина, припухлость, красноречивость, картинность, папула, сочность, экспрессивность

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "выпуклость":
абсолютность, абстрактность, абсурдность, авантажность, авантюрность, аварийность, авиачасть, автентичность, автобиографичность, автоматичность, есть, напасть, пасть, прелесть, странность, субтильность, утонченность, утончённость, учтивость, часть

Рифмы для этого же слова "выпуклость", но если ударение на последний слог :
аббатствовать, абдуцировать, абецедировать, аблактировать, абонировать.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "выпуклость" :
логадясть, тирорость, дйданость, ыивасысть, лоьапасть, лачобюсть, синясисть, вусамасть.


Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Выпуклость" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-В124, для metaphone-"вaпуклaст" и для double-metaphone FPKL.

См. также

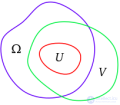... , но при рассмотрении области Рейнхардта можно видеть , что.область сходимости степенного ряда удовлетворяет выпуклости , называемой логарифмически-выпуклой Существуют различные выпуклости области сходимости нескольких комплексных переменных ... ... оболочки получается , если взятьвместо того., чтобы быть множество комплекснозначными полиномиальных функций на G. Полиномиально выпуклая оболочка содержит голоморфно выпуклую оболочку Домен называется голоморфно выпуклым , если для любого ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))

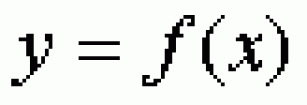... . касательной , проведенной в любой точке этого интервала Точка графика функции , отделяющая выпуклую часть от вогнутой , называется точкой . перегиба Если в интервале , то график функции на этом интервале ... ... в интервале , то график функции на этом интервале вогнутый . Если в интервале , то график функции на этом интервале выпуклый . Если и при переходе через точку xo вторая производная меняет . знак , то точка графика ... (Математический анализ. Дифференциальное исчисление)

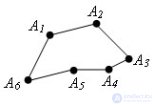... называютсявершинами многоугольника , а звенья – сторонами многоугольника Многоугольник с n вершинами , называется Многоугольник называется выпуклым , если он лежит в одной полуплоскости относительно . любой прямой , содержащей его сторону – выпуклый многоугольник ... (Планометрия)

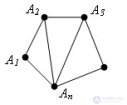... Теорема Сумма углов выпуклого равна 180 °*(n- Доказательство Нужно заметить , n ≥ Для n = 3 многоугольник превращается в треугольник ... (Планометрия)

... нормальное отображение илиbump mapping . - этометод текстурного отображения , используемый дляимитации освещения выпуклостей и.вмятин - реализация bump mapping .Ониспользуется длядобавления деталей безиспользования большего количества ... (Компьютерная графика)

... замкнутых множеств любого антиобменного замыкания образуют антиматроид Неориентированные графы , вкоторых выпуклые множества (подмножества вершин , содержащие все .кратчайшие пути междувершинами вподмножестве ) образуют ... ... равноУдолжен быть элементхне вСчто можно добавить .кСчтобы сформировать другой набор в.Выпуклая геометрия также может быть определена втерминах оператора замыкания .τкоторыйотображает любое ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

---

---