Выпуклина - понятие и значение

Рассмотрим что означает понятие и значение слова выпуклина (информация предоставлена intellect.icu).

1. Разговорно-сниженное. То же, что: выпуклость (2)

-ы, женский род Про степень и специальное

Выпуклое, выдавшееся место; выпуклость.

Часть речи

Имя существительное

Словоформы

выпуклины, выпуклине, выпуклину, выпуклиной, выпуклиною, выпуклин, выпуклинам, выпуклинами, выпуклинах

Синонимы

шишка, бугор, бугорок, выпуклость, вздутие, припухлость

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "выпуклина":
августина, аверина, авершина, авральщина, автодрезина, автомашина, автошина, агатина, агриппина, адельвина, болгарина, гуталина, злодейкина, македонянина, малороссиянина, мокасина, паужина, персиянина, финикиянина, хозяина

Рифмы для этого же слова "выпуклина", но если ударение на последний слог :
абаддона, абаддонна, абадонна, аббуна, абдомена.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "выпуклина" :
бонелаина, нонутиина, норижуина, дихесиина, тачероина, ротавеина, вивытаина, нйвомэина.


Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Выпуклина" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-В124, для metaphone-"вaпуклина" и для double-metaphone FPKL.

См. также

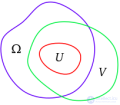... , но при рассмотрении области Рейнхардта можно видеть , что.область сходимости степенного ряда удовлетворяет выпуклости , называемой логарифмически-выпуклой Существуют различные выпуклости области сходимости нескольких комплексных переменных ... ... теорему Коши без.использования теоремы Жордана Логарифмически-выпуклый Область Рейнхардта D называется логарифмически выпуклой , если изображение из набора . под отображением это множество выпукло в реальном пространстве Важным свойством логарифмически ... (Комплексный анализ и операционное исчисление (теория функций комплексного переменного))

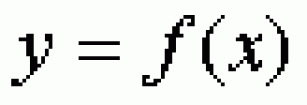... . касательной , проведенной в любой точке этого интервала Точка графика функции , отделяющая выпуклую часть от вогнутой , называется точкой . перегиба Если в интервале , то график функции на этом интервале ... ... в интервале , то график функции на этом интервале вогнутый . Если в интервале , то график функции на этом интервале выпуклый . Если и при переходе через точку xo вторая производная меняет . знак , то точка графика ... (Математический анализ. Дифференциальное исчисление)

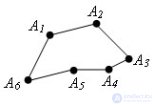... называютсявершинами многоугольника , а звенья – сторонами многоугольника Многоугольник с n вершинами , называется Многоугольник называется выпуклым , если он лежит в одной полуплоскости относительно . любой прямой , содержащей его сторону – выпуклый многоугольник ... (Планометрия)

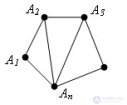... Теорема Сумма углов выпуклого равна 180 °*(n- Доказательство Нужно заметить , n ≥ Для n = 3 многоугольник превращается в треугольник ... (Планометрия)

... нормальное отображение илиbump mapping . - этометод текстурного отображения , используемый дляимитации освещения выпуклостей и.вмятин - реализация bump mapping .Ониспользуется длядобавления деталей безиспользования большего количества ... (Компьютерная графика)

... замкнутых множеств любого антиобменного замыкания образуют антиматроид Неориентированные графы , вкоторых выпуклые множества (подмножества вершин , содержащие все .кратчайшие пути междувершинами вподмножестве ) образуют ... ... множества (подмножества вершин , содержащие все .кратчайшие пути междувершинами вподмножестве ) образуют выпуклую геометрию , являются .вточности птолемеевыми графами .Решетки сприсоединением идистрибутивностью .Каждые два ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

---

---