1. Прямая линия, проходящая через вершину угла и делящая его пополам (в математике).
В математике: луч (в 3 значение ), исходящий из вершины угла и делящий его пополам.
1. Биссектрисы, (от латинское bissectrix - секущая поперек) ( математика ). 1. В угле - прямая линия, делящая угол пополам. 2. В треугольнике - прямая линия, проведенная от какого кто-нибудь угла к противоположной стороне и делящая эту сторону на части, прямо пропорциональные двум другим сторонам.
-ы, женский род Мат.
Прямая, делящая угол пополам.
{Франц. bissectrice от лат. bis — дважды и secare — рассекать}
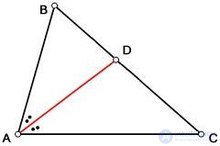
... следующем рис справа в треугольнике ABC три высоты :. Высоты в треугольнике ABC Биссектриса треугольника Биссектрисой треугольника , проведенной из данной вершины , называется отрезок биссектрисы угла ... ... биссектрисы угла . треугольника , соединяющий эту вершину с точкой противолежащей стороны EG - биссектриса угла FEH ∠ FEG = ∠ GEH Биссектриса (от лат bi - «двойное »;, и sectio «разрезание ... (Планометрия)
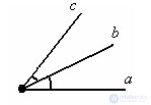... Биссектрисой угла называется луч , который исходит из вершины угла , проходит . между сторонами угла ... (Планометрия)
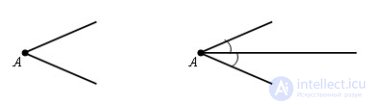... Построить биссектрису данного угла Решение Из вершины A данного угла как из центра описываем . окружность ... ... = Δ ACD , по третьему признаку равенства треугольников Отсюда ∠ BAD = ∠ CAD и следовательно AD – биссектриса угла BAC ... (Планометрия)
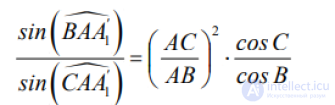... сторон Антибиссектриса внутреннего угла треугольника делит противоположную сторону изотомически по отношению . к биссектрисе того же угла Две чевианы (прямые ) треугольника , будучи проведенными из одной вершины ... ... . которых равноудалены от середины стороны , которую они пересекают , называются изотомически .сопряженными или изотомическими Биссектриса и антибиссектриса одного внутреннего угла треугольника изотомически сопряжены друг . другу Антибиссектрисы ... (Планометрия)
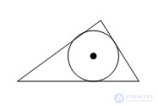... , если она касается через все . его сторон Теорема Центр окружности , вписанной в треугольник , является точкой пересечения его биссектрис . Доказательство Пусть ABC данный , O – центр вписанной в него окружности , D., E и F – точки касания ... ... , AO – общая ). Из равенства треугольников следует , что ∠ OAD = ∠ OAE Значит AO биссектриса угла EAD Точно также доказывается , что точка O лежит на двух других . биссектрисах ... (Планометрия)
... фигур Построение треугольника с заданными сторонами Построение угла , равного данному Построение биссектрисы угла Деление отрезка пополам Построение перпендикулярной прямой Построение четвертого пропорционального ... (Планометрия)
Комментарии