Спектральное представление сигналов кратко

Привет, Вы узнаете о том , что такое Спектральное представление сигналов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Спектральное представление сигналов , настоятельно рекомендую прочитать все из категории Теория сигналов и линейных систем.

Кроме привычного динамического представления сигналов и функций в виде зависимости их значений от определенных аргументов (времени, линейной или пространственной координаты и т.п.) при анализе и обработке данных широко используется математическое описание сигналов по аргументам, обратным аргументам динамического представления. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой сколь угодно сложный по своей форме сигнал, не имеющий разрывов второго рода (бесконечных значений на интервале своего задания), можно представить в виде суммы более простых сигналов, и, в частности, в виде суммы простейших гармонических колебаний, что выполняется при помощи преобразования Фурье. Соответственно, математически разложение сигнала на гармонические составляющие описывается функциями значений амплитуд и начальных фаз колебаний по непрерывному или дискретному аргументу – частоте изменения функций на определенных интервалах аргументов их динамического представления. Совокупность амплитуд гармонических колебаний разложения называют амплитудным спектром сигнала, а совокупность начальных фаз – фазовым спектром. Об этом говорит сайт https://intellect.icu . Оба спектра вместе образуют полный частотный спектр сигнала, который по точности математического представления тождественен динамической форме описания сигнала.

Линейные системы преобразования сигналов описываются дифференциальными уравнениями, причем для них верен принцип суперпозиции, согласно которому реакция систем на сложный сигнал, состоящий из суммы простых сигналов, равна сумме реакций от каждого составляющего сигнала в отдельности. Это позволяет при известной реакции системы на гармоническое колебание с определенной частотой определить реакцию системы на любой сложный сигнал, разложив его в ряд гармоник по частотному спектру сигнала. Широкое использование гармонических функций при анализе сигналов объясняется тем, что они являются достаточно простыми ортогональными функциями и определены при всех значениях непрерывных переменных. Кроме того, они являются собственными функциями времени, сохраняющими свою форму при прохождении колебаний через любые линейные системы и системы обработки данных с постоянными параметрами (изменяются только амплитуда и фаза колебаний). Немаловажное значение имеет и то обстоятельство, что для гармонических функций и их комплексного анализа разработан мощный математический аппарат.

Примеры частотного представления сигналов приводятся ниже (рис. 1.1.5 – 1.1.12).

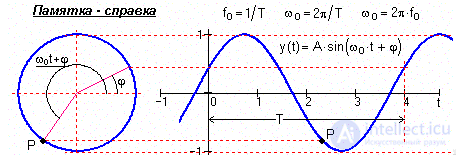
Рис. 1.1.5

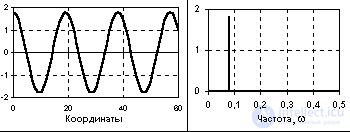
Рис. 1.1.6 отрезок периодической сигнальной функции,

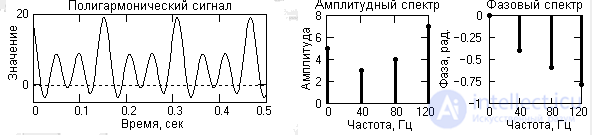
Рис. 1.1.7 Частотное представление данного сигнала (спектр сигнала)

Рис. 1.1.8 Прямоугольный периодический сигнал (меандр).

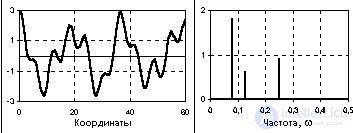
Рис. 1.1.9

Рис. 1.1.10. Апериодический сигнал и модуль спектра

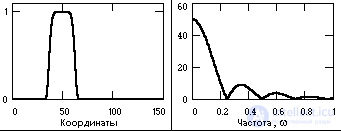
Рис. 1.1.11. Импульсный сигнал и модуль спектра.

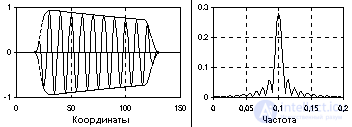
Рис. 1.1.12 Пример радиоимпульса

Кроме гармонического ряда Фурье применяются и другие виды разложения сигналов: по функциям Хартли, Уолша, Бесселя, Хаара, полиномам Чебышева, Лаггера, Лежандра и др. Главное условие однозначности и математической идентичности отображения сигналов - ортогональность функций разложения. Но при качественном анализе сигналов могут применяться и неортогональные функции, выявляющие какие-либо характерные особенности сигналов, полезные для интерпретации физических данных.

Исследование, описанное в статье про Спектральное представление сигналов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Спектральное представление сигналов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория сигналов и линейных систем