Математическое описание сигналов кратко

Привет, Вы узнаете о том , что такое Математическое описание сигналов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Математическое описание сигналов , настоятельно рекомендую прочитать все из категории Теория сигналов и линейных систем.

Сигналы могут быть объектами теоретических исследований и практического анализа только в том случае, если указан способ их математического описания - математическая модель сигнала. Математическое описание позволяет абстрагироваться от физической природы сигнала и материальной формы его носителя, проводить классификацию сигналов, выполнять их сравнение, устанавливать степень тождества, моделировать системы обработки сигналов. Как правило, описание сигнала задается функциональной зависимостью определенного информационного параметра сигнала от независимой переменной (аргумента) – s(х), y(t) и т.п. Такая форма описания и графического представления сигналов называется динамической (сигнал в реальной динамике его поведения по аргументам). Функции математического описания сигналов могут быть как вещественными, так и комплексными. Выбор математического аппарата описания определяется простотой и удобством его использования при анализе и обработке сигналов.

Отметим двойственность применения описания сигналов функциями типа s(t) и т.п. С одной стороны s(t) – это величина, равная значению функции в момент времени t. С другой стороны мы обозначаем через s(t) и саму функцию, т.е. то правило, по которому каждому значению t ставится в соответствие определенная величина s. В большинстве аналитических выражений это не вызывает недоразумений и при однозначном соответствии значений сигналов их аналитическим выражениям принимается по умолчанию.

Сделаем также одно замечание по терминологии описания сигналов. В теоретических работах по анализу сигналов конкретные значения величины сигнала (отсчеты значений по аргументу) часто именуют координатами сигнала. В отраслях знаний, связанных с геологией и горным делом, и в геофизической практике в том числе, этот термин используется по своему прямому смысловому назначению – пространственных координат результатов измерений, и является неизменным атрибутом всех геолого-геофизических данных. С учетом последнего фактора условимся применять термин “координата” по своему традиционному смысловому назначению в качестве обобщающего термина для независимых переменных сигнальных функций. При этом под понятием координат значений сигнала будем понимать не только какие-либо пространственные координаты, как это непосредственно имеет место для результатов измерений при геолого-геофизических съемках, но и любые другие аргументы, на числовой оси которых отложены значения или отсчеты сигнала и рассматривается динамика его изменения (пример на рис. 1.1.1)

Способы представления сигналов. Гармоническое колебание

Гармоническим называется колебание, которое описывается гармонической функцией времени: sin(t), cos(t).
Сигналы произвольной формы могут иметь следующие формы
представления:

• - временное представление сигнала;
• - комплексное представление;
• - векторное представление;
• - спектральное;
• - операторное

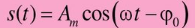
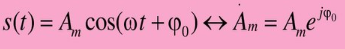
. Об этом говорит сайт https://intellect.icu .

Спектральное представление сигналов

Спектральный способ представления сигнала s(t) основан на представлении любой функции времени совокупностью (суммой) гармонических составляющих с соответствующими амплитудами, частотами и начальными фазами.
При спектральном представлении сигнал задается не как функция времени, а как функция частоты, что является очень удобным, поскольку свойства электрических цепей часто задаются их частотными характеристиками

Спектры периодических сигналов

Сигналы, удовлетворяющие условию S(t)=S(t+T), если Т < ∞, а -∞<t<+∞ называются периодическими.
Простейшим периодическим сигналом являются гармоническое сигнал S(t)=A_mcos(ω₀t+ φ₀).

Он состоит из одной гармонической составляющей с амплитудой Am и начальной фазой φ0, которые расположены на частоте ω₀.
Для наглядного изображения спектры сигналов изображают в виде графиков, Различают два вида спетров амплитудный спектр и фазовый спектр.
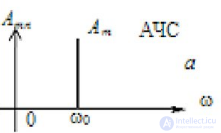
Амплитудным или амплитудно-частотным спектром (АЧС) называется зависимость амплитуд гармонических составляющих от частоты
(АЧС→Amn(ω), рис 2.,а).

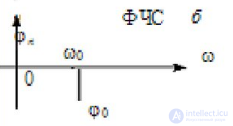
Фазово-частотным спектром (ФЧС) называется зависимость начальных фаз гармонических составляющих от частоты
(ФЧС→ (ω), рис. 2,б).

Спектр произвольного периодического сигнала

Из математики известно, что любой периодический сигнал s(t), удовлетворяющий условиям Дирихле, может быть представлен тригонометрическим рядом Фурье

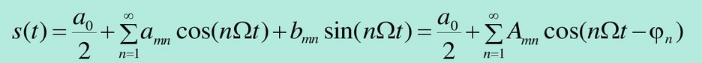
где 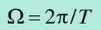– основная частота следования сигнала (первая гармоника сигнала),

n – номер гармоники сигнала,

nΩ – частота n-й гармоники сигнала,

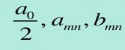– коэффициенты ряда Фурье:

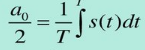– постоянная (средняя) составляющая сигнала;

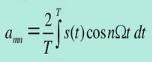– косинус составляющая амплитуды n-й гармоники спектра сигнала;

– синус составляющая амплитуды гармоники спектра сигнала;

– амплитуда n-й гармоники;
– начальная фаза n-й гармоники.

Спектр периодического сигнала имеет дискретный характер

Спектры непериодических сигналов

Непериодический сигнал в ряд Фурье разложить нельзя. Для него вводят интеграл Фурье, который является пределом ряда, когда (T→∞). При этом:

1) основная частота сигнала 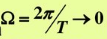., т.е. расстояние между линиями спектра, равное Ω становится бесконечно малым, а спектр – сплошным.

2) амплитуды гармонических составляющих 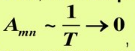, т.е. спектр состоит из гармонических составляющих с бесконечно малыми амплитудами.
Спектр непериодического сигнала характеризуется функцией спектральной плотности амплитуд, т.е. плотность распределения бесконечно малых амплитуд
по оси частот. Плотность это число составляющих в диапазоне частот в 1 Гц.
Спектральная плотность S(jω) связана с сигналом s(t) преобразованием Фурье:

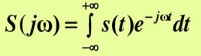– прямое преобразование Фурье (ППФ).
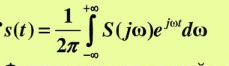– обратное преобразование Фурье (ОПФ).
Функция спектральной плотности – это комплексная функция частоты S(jω) = S(ω)e ^jφ(ω), где S(ω) – модуль функции спектральной плотности, или его называют спектральной плотностью амплитуд,
φ(ω) – аргумент функции спектральной плотности – спектр фаз.
Спектра непериодического сигнала имеет сплошной, непрерывный характер.

Операторное представление сигнала

Преобразование Фурье применяется для сигналов s(t) с конечной энергией, т. е. для сигналов, удовлетворяющих условию. Функция s(t), удовлетворяющая такому условию, называется абсолютно интегрируемой.

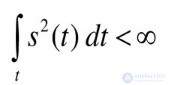
• Более универсальным является операторное представление сигнала, которое основано на преобразовании Лапласа.
• При операторном представлении сигналу s(t) - функции действительной переменной t, ставится в соответствие функция S(p) комплексной переменной р ,

где p = σ + jω называется комплексной частотой.
Связь между ними в виде преобразования Лапласа:

прямое преобразование Лапласа , (S(p) = L[s(t)])
обратное преобразование Лапласа ,

Сигнал s(t) называют оригиналом, а S(p) – изображением, или операторным представлением сигнала.
Для нахождения функции спектральной плотности амплитуд S(jω)сигнала S(t), по известному операторному представлению S(p), необходимо в последнем
оператор р заменить на jω, то есть

Исследование, описанное в статье про Математическое описание сигналов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Математическое описание сигналов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория сигналов и линейных систем