Основные свойства энтропии кратко

Привет, Вы узнаете о том , что такое Основные свойства энтропии, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое Основные свойства энтропии , настоятельно рекомендую прочитать все из категории Теория сигналов и линейных систем.

1. Энтропия является величиной вещественной и неотрицательной, т.к. значения вероятностей p_n находятся в интервале 0-1, значения log p_n всегда отрицательны, а значения -p_n log p_n в (1.4.2) соответственно положительны.

2. Энтропия - величина ограниченная, т.к. при p_n Ю 0 значение -p_nЧ log p_n также стремится к нулю, а при 0 < p_n Ј 1 ограниченность суммы всех слагаемых очевидна.

3. Энтропия равна 0, если вероятность одного из состояний источника информации равна 1, и тем самым состояние источника полностью определено (вероятности остальных состояний источника равны нулю, т.к. сумма вероятностей должна быть равна 1).

4. Энтропия максимальна при равной вероятности всех состояний источника информации:

H_max(U) = -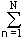(1/N) log(1/N) = log N.

5. Энтропия источника с двумя состояниями u₁ и u₂ при изменении соотношения их вероятностей p(u₁)=p и p(u₂)=1-p определяется выражением:

H(U) = -[p log p + (1-p) log(1-p)],

и изменяется от 0 до 1, достигая максимума при равенстве вероятностей. Об этом говорит сайт https://intellect.icu . График изменения энтропии приведен на рис. 1.4.1.

6. Энтропия объединенных статистически независимых источников информации равна сумме их энтропий.

Рассмотрим это свойство на двух источниках информации u и v. При объединении источников получаем обобщенный источник информации (u,v), который описывается вероятностями p(u_nv_m) всех возможных комбинаций состояний u_n источника u и v_m источника v. Энтропия объединенного источника при N возможных состояниях источника u и М возможных состояниях источника v:

H(UV) = -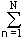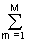p(u_nv_m) log p(u_nv_m),

Источники статистически независимы друг от друга, если выполняется условие:

p(u_nv_m) = p(u_n)Ч p(v_m).

С использованием этого условия соответственно имеем:

H(UV) = -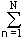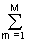p(u_n)p(v_m) log [p(u_n)p(v_m)] =

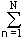= -p(u_n) log p(u_n)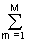p(v_m) -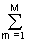p(v_m) log p(v_m)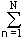p(u_m).

С учетом того, что 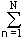p(u_n) = 1 и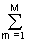p(v_m) = 1, получаем:

H(UV) = H(U) + H(V). (1.4.3)

7. Энтропия характеризует среднюю неопределенность выбора одного состояния из ансамбля, полностью игнорируя содержательную сторону ансамбля. С одной стороны, это расширяет возможности использования энтропии при анализе самых различных явлений, но, с другой стороны, требует определенной дополнительной оценки возникающих ситуаций. Как это следует из рис. 1.4.1, энтропия состояний может быть неоднозначной, и если в каком-либо экономическом начинании действие u с вероятностью p_u=p приводит к успеху, а действие v с вероятностью p_v=1-p к банкротству, то выбор действий по оценке энтропии может оказаться и прямо противоположным, т.к. энтропия при p_v=p равна энтропии при p_u=p.

Исследование, описанное в статье про Основные свойства энтропии, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое Основные свойства энтропии и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теория сигналов и линейных систем