Лекция Тесты
Привет, мой друг, тебе интересно узнать все про тесты по рядам, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое тесты по рядам, задачи с решениями по рядам , настоятельно рекомендую прочитать все из категории Ряды. Кликните на вариант (или варианты ответов), если он правильный - то будет подсвечен зеленым цветом и вам будет зачислено пару монеток, а если неверный - то красным и будет снята монетка. Удачи в прохождении онлайн теста!
Ряд, называемый также бесконечная сумма — одно из центральных понятий математического анализа.
Исследовать ряд на сходимость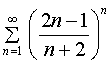 
.
Решение.
Находим
Так как 2 > 1, то, по признаку Коши, ряд расходится.
Ответ: ряд расходится.
Исследовать на сходимость ряд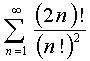 
.
Решение.
Так как в Un присутствуют факториалы, используем признак Даламбера.
Следовательно, по признаку Даламбера ряд расходится.
Ответ: ряд расходится.
Исследовать на сходимость ряд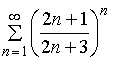 
.
Решение.
Признак Коши в этом случае не работает, так как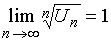 
. Здесь применим необходимый признак сходимости рядов.
Следовательно, по необходимому признаку ряд расходится.
Ответ: ряд расходится.
Исследовать на сходимость ряд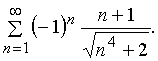 
Решение.
Составим ряд из модулей членов нашего ряда:
получим знакоположительный ряд.
Применим предельный признак сравнения. Составим ряд эквивалентный ряду (*):
ряды эквивалентны. Так как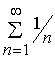 
- расходится, то ряд (*) также расходится. Следовательно, исходный ряд не сходится абсолютно.
Исследуем на условную сходимость по признаку Лейбница:
следовательно, наш ряд сходится условно.
Ответ: ряд сходится условно.
Найти интервал сходимости ряда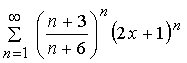 
.
Решение.
Выполнив замену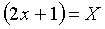 
, получаем ряд 
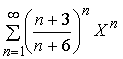. Об этом говорит сайт https://intellect.icu . Находим радиус сходимости:
,
Следовательно,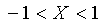 
, выполнив обратную замену, получаем 
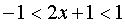. Решаем неравенство: 
, 
.
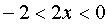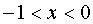Проверим сходимость ряда на границах интервала сходимости:
Следовательно, ряд сходится абсолютно при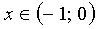 
, во всех остальных точках он расходится.
Ответ: ряд сходится абсолютно при
Вычислить интеграл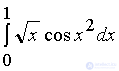 
с точностью до 0,001.
Решение.
Используя ряд Маклорена функции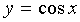 
:
Выражаем функцию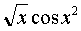 
через функциональный ряд:
Так как областью сходимости данного ряда является интервал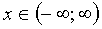 
и интервал 
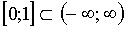, то интегрируя полученный ряд почленно, находим:
Получен знакочередующийся ряд, следовательно, ошибка в вычислении суммы не превышает модуля первого отброшенного члена ряда. Найдем член ряда, величина которого меньше 0,001:
Следовательно, для достижения требуемой точности необходимо отбросить член ряда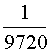 
и все последующие:
Ответ:
1. Для исследования положительных числовых рядов на сходимость не используют признак
2. 
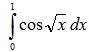Вычислить интеграл, указанный на рисунке, приближенно с точностью до 0,01 путем разложения подынтегральной функции в степенной ряд
3. С помощью степенных рядов приближенно не находят
4. Частичной суммой Sn ряда называется сумма его
5. Радиус R сходимости степенного ряд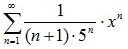а 
6. Признак Даламбера рассматривает сходимость
7. Данный числовой ряд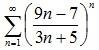 
8. Данный числовой ряд 
9. Интервал сходимости степенного ряда вычисляется с помощью теоремы
10. Область сходимости степенного ряда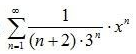 
Тебе нравиться тесты по рядам? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое тесты по рядам, задачи с решениями по рядам и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Ряды
Из статьи мы узнали кратко, но содержательно про тесты по рядам
Комментарии