Исследование рядов на сходимость 5.1.3. Необходимый признак сходимости числового ряда кратко

Привет, мой друг, тебе интересно узнать все про необходимый признак сходимости числового ряда, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое необходимый признак сходимости числового ряда, сходимость рядов , настоятельно рекомендую прочитать все из категории Ряды.

Исследование рядов на сходимость

Одной из ключевых задач темы является исследование ряда на сходимость. При этом возможны два случая:

1) Ряд расходится. Это значит, что бесконечная сумма равна бесконечности: 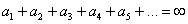либо суммы вообще не существует, как, например, у ряда
(вот, кстати, и пример ряда с отрицательными членами). Хороший образец расходящегося числового ряда встретился в начале урока: 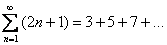. Здесь совершенно очевидно, что каждый следующий член ряда больше, чем предыдущий, поэтому 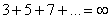и, значит, ряд расходится. Еще более тривиальный пример: .

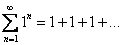2) Ряд 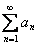сходится. Это значит, что бесконечная сумма равна некоторому конечному числу 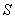: 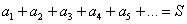. Об этом говорит сайт https://intellect.icu . Пожалуйста: 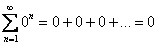– этот ряд сходится и его сумма равна нулю. В качестве более содержательного примера можно привести бесконечно убывающую геометрическую прогрессию, известную нам еще со школы: 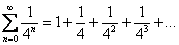. Сумма членов бесконечно убывающей геометрической прогрессии рассчитывается по формул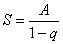е: , где – первый член прогрессии, а – ее основание, которое, как правило, записывают в виде правильной дроби. В данном случае: , 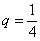. Таким образом: 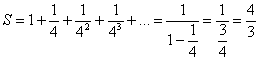Получено конечное число, значит, ряд 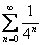сходится, что и требовалось доказать.

Однако в подавляющем большинстве случаев найти сумму ряда не так-то просто, и поэтому на практике для исследования сходимости ряда используют специальные признаки, которые доказаны теоретически.

Существует несколько признаков сходимости ряда: необходимый признак сходимости ряда, признаки сравнения, признак Даламбера, признаки Коши, признак Лейбница и некоторые другие признаки. Когда какой признак применять? Это зависит от общего члена ряда , образно говоря – от «начинки» ряда. И очень скоро мы все разложим по полочкам.

5.1.3. необходимый признак сходимости числового ряда

Если ряд 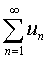сходится, то .

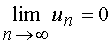Таким образом, если установлено, что , то ряд 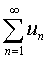расходится.

Если установлено, что 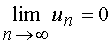, то о сходимости ряда ничего сказать нельзя. Ряд может как сходиться, так и расходиться. В данном случае требуется дальнейшее исследование сходимости ряда.

Тебе нравиться необходимый признак сходимости числового ряда? или у тебя есть полезные советы и дополнения? Напиши другим читателям ниже. Надеюсь, что теперь ты понял что такое необходимый признак сходимости числового ряда, сходимость рядов и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Ряды