16: ПОПАРНОЕ СОПОСТАВЛЕНИЕ В ЭКСПЕРТНОМ МЕТОДЕ кратко

Привет, Вы узнаете о том , что такое попарное сопоставление в экспертном методе, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое попарное сопоставление в экспертном методе , настоятельно рекомендую прочитать все из категории Квалиметрия надежность и качество.

Вопросы лекции:

1. Попарное сопоставление объектов

2. Двойное попарное сопоставление объектов

3. Ранжирование в методе попарного сопоставления

1. Попарное сопоставление объектов

Экспертное оценивание при попарном сопоставлении рассматриваемых объектов осуществляют, если количество объектов

четное. При этом предпочтение эксперта выражается указанием

номера предпочтительного объекта в соответствующей графе

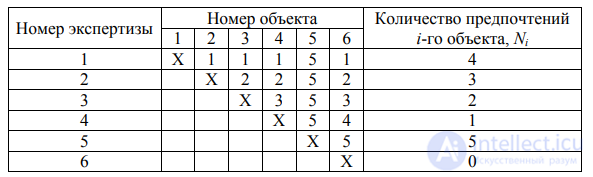
таблицы сопоставления, как это показано, например, для шести

объектов в табл. 10.

Таблица 10 Результаты попарного сопоставления объектов экспертом

Максимально возможное число предпочтений любого из рассматриваемых объектов, полученное от одного из экспертов,

равно N = m-1,

где т - количество оцениваемых объектов.

Частота этих предпочтений Fi находится как частное от деления Ni на Nmax, т.е.

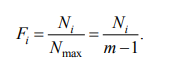
Используя данные табл. 10, получаем Nmax = 6 - 1 = 5, а частоты предпочтений, данные экспертом, равны:

F1 = 4/5 = 0,8; F2 = 3/5 = 0,6; F3 = 2/5 = = 0,4; F4 = 1/5 = 0,2; F5 = 5/5 = 1; F6 = 0/5 = 0.

Общее число суждений одного эксперта С, связанное

с количеством объектов экспертизы т, находят из соотношения

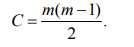
При шести объектах экспертизы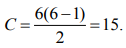

Определенный одним экспертом показатель i-го объекта или весомость по сравнению с другими объектами рассчитывают по формуле:

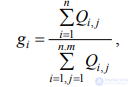
где n - количество экспертов;

т - число оцениваемых показателей;

Qi,j - коэффициент весомости j-го показателя в рангах (баллах), который дал i-й эксперт.

Преобразованной к виду:

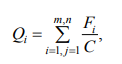
где п - число экспертов в группе;

Fi - частота предпочтения объектов;

C - количество возможных суждений одного эксперта

Пусть число экспертов в группе равно пяти и их оценки о Fi. Об этом говорит сайт https://intellect.icu . сведены в табл. 11.

Таблица 11 Частоты предпочтений объектов, данные экспертами

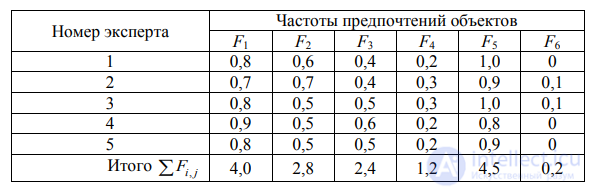
В данном случае результаты экспертизы по определению показателей объектов таковы:

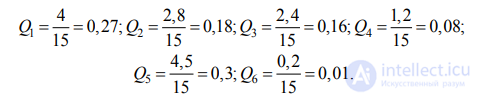
Найдем сумму значений показателей весомости:

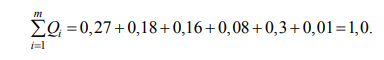
Этот результат свидетельствует о том, что показатели оценены экспертами достаточно точно. Поэтому, очевидно, что итоговый ранжированный ряд объектов рассмотрения по их показателями имеет вид:

№ 6 < № 4 < № 3 < № 2 < № 1 < № 5.

2. Двойное попарное сопоставление объектов

Если сумма показателей весомости существенно отличается от 1, то, чтобы увеличить достоверность оценивания, проводят повторное сопоставление объектов, используя для этого свободную часть таблицы попарного сопоставления. При этом повторное сопоставление производят в хаотическом порядке. В таком случае

каждая пара объектов сопоставляется дважды. Такое полное или двойное сопоставление объектов существенно уменьшает случайные ошибки оценок экспертов. Следовательно, двойное сопоставление обладает более высокой достоверностью, чем однократное.

Пусть после двойного сопоставления и установления предпочтений получены результаты оценок одного эксперта представленные в табл. 12.

Таблица 12 Результаты двойного попарного сопоставления объектов экспертом

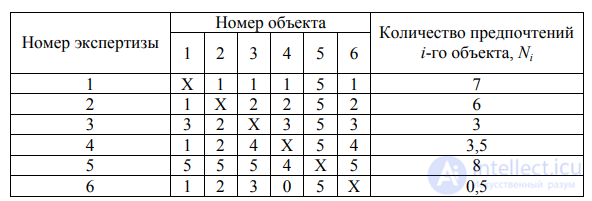
Примечание. Если сопоставляемые объекты одинаковы, равны между собой, то это обозначается цифрой 0, но обоим объектам дается по

0,5 предпочтения.

Возможное наибольшее количество предпочтений одного объекта равно

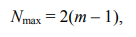
а частота предпочтений

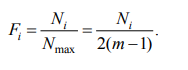
, где Ni - количество предпочтений i-го объекта, Nmax - наибольшее количество предпочтений.

По данным таблицы 12 находим, что при Nmax = 10.

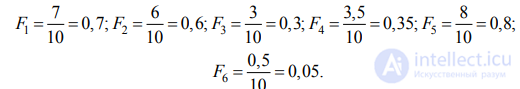
Показатели оцениваемых объектов находим по формуле:

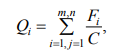
, где п - число экспертов в группе

При условии, что в случае двойного попарного сопоставления количество возможных суждений одного эксперта равно

С = т (т - 1). В рассматриваемом нами примере С = 6 (6 - 1) = 30.

Поэтому «усредненные» показатели оцениваемых объектов таковы:

Полученные результаты являются приведенными значениями оценок фактического, реального попарного сопоставления

рассматриваемых объектов.

Сумма значений всех показателей равна:

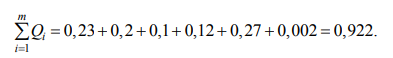
Ранжированный ряд объектов, составленный по оценкам первого эксперта, такой:

Q6 < Q3 < Q4 < Q2 < Q1 < Q5 .

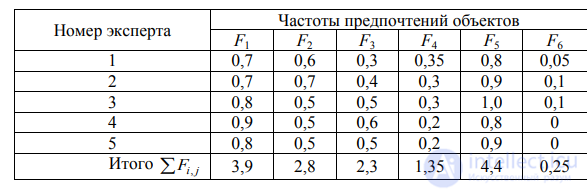
Если, например, остальные четыре эксперта дали оценки такие же, как приведены в табл. 11, то в табл. 13 будет изменена, по сравнению с табл. 11, только первая строка.

Таблица 13 Свод частот предпочтений объектов

Итоговый результат экспертизы всех экспертов, рассчитываемый по формуле:

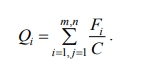
где п - число экспертов в группе

В данном примере будет таким:

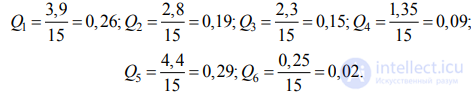
Сумма всех показателей весомости или значимости (качества) равна:

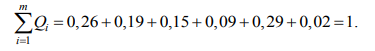
Следовательно, ранжированный ряд по данным экспертизы имеет вид:

Q6 < Q4 < Q3 < Q2 < Q1 < Q5 .

Таким образом получают результаты экспертизы при двойном попарном сопоставлении оцениваемых объектов.

3. Ранжирование в методе попарного сопоставления

Как видно из вышепредставленного примера, метод ранжирования постоянно реализуется в процессе применения метода

попарного сопоставления

Анализ данных, представленных в статье про попарное сопоставление в экспертном методе, подтверждает эффективность применения современных технологий для обеспечения инновационного развития и улучшения качества жизни в различных сферах. Надеюсь, что теперь ты понял что такое попарное сопоставление в экспертном методе и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Квалиметрия надежность и качество

Из статьи мы узнали кратко, но содержательно про попарное сопоставление в экспертном методе

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.