Лекция
Привет, Вы узнаете о том , что такое кристаллическая структура, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое кристаллическая структура, кристаллическая решетка, дефекты кристалла , настоятельно рекомендую прочитать все из категории Материаловедение и материалы электронных аппаратов.
кристаллическая структура — такая совокупность атомов, в которой с каждой точкой кристаллической решетки связана определенная группа атомов, называемая мотивной единицей, причем все такие группы одинаковые по составу, строению и ориентации относительно решетки. Можно считать, что структура возникает в результате синтеза решетки и мотивной единицы, в результате размножения мотивной единицы группой трансляции.
кристаллическая решетка — вспомогательный геометрический образ, вводимый для анализа строения кристалла. Решетка имеет сходство с канвой или сеткой, что дает основание называть точки решетки узлами. Решеткой является совокупность точек, которые возникают из отдельной произвольно выбранной точки кристалла под действием группы трансляции. Это расположение замечательно тем, что относительно каждой точки все остальные расположены совершенно одинаково. Применение к решетке в целом любой из присущих ей трансляций приводит к ее параллельному переносу и совмещению. Для удобства анализа обычно точки решетки совмещают с центрами каких-либо атомов из числа входящих в кристалл, либо с элементами симметрии.
В зависимости от пространственной симметрии, все кристаллические решетки подразделяются на семь кристаллических систем. По форме элементарной ячейки они могут быть разбиты на шесть сингоний. Все возможные сочетания имеющихся в кристаллической решетке поворотных осей симметрии и зеркальных плоскостей симметрии приводят к делению кристаллов на 32 класса симметрии, а с учетом винтовых осей симметрии и скользящих плоскостей симметрии на 230 пространственных групп.
Помимо основных трансляций, на которых строится элементарная ячейка, в кристаллической решетке могут присутствовать дополнительные трансляции, называемые решетками Браве.
В простейшем случае мотивная единица состоит из одного атома, например в кристаллах меди или железа. Возникающая на основе такой мотивной единицы структура геометрически весьма сходна с решеткой, но все же отличается тем, что составлена атомами, а не точками. Часто это обстоятельство не учитывают, и термины «кристаллическая решетка» и «кристаллическая структура» для таких кристаллов употребляются как синонимы, что нестрого. В тех случаях, когда мотивная единица более сложна по составу — состоит из двух или большего числа атомов, геометрического сходства решетки и структуры нет, и смешение этих понятий приводит к ошибкам. Так, например, структура магния или алмаза не совпадает геометрически с решеткой: в этих структурах мотивные единицы состоят из двух атомов.
Основными параметрами, характеризующими кристаллическую структуру, некоторые из которых взаимосвязаны, являются следующие:
В кристаллографии , кристаллическая структура представляет собой описание упорядоченного расположения атомов , ионов или молекул в кристаллическом материале . Упорядоченные структуры возникают из внутренней природы составляющих частиц и образуют симметричные узоры, которые повторяются в основных направлениях трехмерного пространства в материи.

Наименьшая группа частиц в материале, составляющая этот повторяющийся узор, - это элементарная ячейка структуры. Элементарная ячейка полностью отражает симметрию и структуру всего кристалла, который построен до повторяющегося перевода элементарной ячейки вдоль его главных осей. Векторы трансляции определяют узлы решетки Браве .
Длины главных осей или краев элементарной ячейки и углы между ними являются постоянными решетки , также называемыми параметрами решетки или параметрами ячейки . В симметрии свойство кристалла описывается концепцией пространственных групп . Все возможные симметричные расположения частиц в трехмерном пространстве могут быть описаны 230 пространственными группами .
Кристаллическая структура и симметрия играют решающую роль в определении многих физических свойств, таких как спайность , электронная зонная структура и оптическая прозрачность .
Кристаллическая структура описывается с точки зрения геометрии расположения частиц в элементарной ячейке. Элементарная ячейка определяется как наименьшая повторяющаяся единица, имеющая полную симметрию кристаллической структуры. Геометрия элементарной ячейки определяется как параллелепипед , обеспечивающий шесть параметров решетки, взятых как длины краев ячейки ( a , b , c ) и углы между ними (α, β, γ). Положение частиц внутри элементарной ячейки описывается дробными координатами ( x i , y i , z i) по краям ячейки, отсчитываемой от контрольной точки. Необходимо указать только координаты наименьшего асимметричного подмножества частиц. Эта группа частиц может быть выбрана так, чтобы она занимала наименьшее физическое пространство, а это означает, что не все частицы должны физически располагаться внутри границ, задаваемых параметрами решетки. Все остальные частицы элементарной ячейки генерируются операциями симметрии, которые характеризуют симметрию элементарной ячейки. Совокупность операций симметрии элементарной ячейки формально выражается как пространственная группа кристаллической структуры.
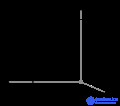
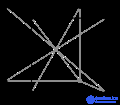
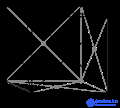
Векторы и плоскости в кристаллической решетке описываются трехзначным индексом Миллера . Этот синтаксис использует индексы ℓ , m и n в качестве параметров направления.
По определению, синтаксис ( ℓmn ) обозначает плоскость, которая пересекает три точки a 1 / ℓ , a 2 / m и a 3 / n или несколько их кратных. То есть индексы Миллера пропорциональны обратным точкам пересечений плоскости с элементарной ячейкой (в базисе векторов решетки). Если один или несколько индексов равны нулю, это означает, что плоскости не пересекают эту ось (т. Е. Точка пересечения находится «на бесконечности»). Плоскость, содержащая ось координат, перемещается так, что она больше не содержит эту ось до определения ее индексов Миллера. Индексы Миллера для плоскости - целые числабез общих факторов. Отрицательные показатели обозначаются горизонтальными полосами, как в (1 2 3). В ортогональной системе координат для кубической ячейки индексы Миллера плоскости являются декартовыми компонентами вектора, нормального к плоскости.
Если рассматривать только ( ℓmn ) плоскости, пересекающие одну или несколько точек решетки ( плоскости решетки ), расстояние d между соседними плоскостями решетки связано с (кратчайшим) вектором обратной решетки, ортогональным плоскостям, по формуле
Кристаллографические направления - это геометрические линии, соединяющие узлы ( атомы , ионы или молекулы ) кристалла. Точно так же кристаллографические плоскости представляют собой геометрические плоскости, соединяющие узлы. Некоторые направления и плоскости имеют более высокую плотность узлов. Эти плоскости с высокой плотностью влияют на поведение кристалла следующим образом:
Некоторые направления и плоскости определяются симметрией кристаллической системы. В моноклинной, ромбоэдрической, тетрагональной и тригонально-гексагональной системах есть одна уникальная ось (иногда называемая главной осью ), которая имеет более высокую вращательную симметрию, чем две другие оси. Базисная плоскость является плоскостью , перпендикулярной главной оси в этих кристаллических системах. Для триклинных, орторомбических и кубических кристаллических систем обозначение оси произвольное, главная ось отсутствует.
В частном случае простых кубических кристаллов векторы решетки ортогональны и имеют одинаковую длину (обычно обозначаются a ); аналогично для обратной решетки. Таким образом, в этом общем случае индексы Миллера ( ℓmn ) и [ ℓmn ] просто обозначают нормали / направления в декартовых координатах . Для кубических кристаллов с постоянной решетки a расстояние d между соседними (ℓmn) плоскостями решетки равно (сверху):
Из-за симметрии кубических кристаллов можно менять место и знак целых чисел и иметь эквивалентные направления и плоскости:
Для гранецентрированной кубической (ГЦК) и объемноцентрированной кубической (ОЦК) решеток векторы примитивной решетки не ортогональны. Однако в этих случаях индексы Миллера обычно определяются относительно векторов решетки кубической сверхъячейки и, следовательно, снова являются просто декартовыми направлениями .
Расстояние d между соседними ( hkℓ ) плоскостями решетки определяется выражением
Определяющим свойством кристалла является присущая ему симметрия. Выполнение определенных операций симметрии с кристаллической решеткой не меняет ее. Все кристаллы обладают трансляционной симметрией в трех направлениях, но некоторые имеют и другие элементы симметрии. Например, поворот кристалла на 180 ° вокруг определенной оси может привести к атомной конфигурации, идентичной исходной конфигурации; кристалл имеет двойную вращательную симметрию относительно этой оси. В дополнение к вращательной симметрии кристалл может иметь симметрию в виде зеркальных плоскостей, а также так называемые составные симметрии, которые представляют собой комбинацию трансляционной и вращательной или зеркальной симметрии. Полная классификация кристалла достигается, когда идентифицированы все присущие кристаллу симметрии.
Решетчатые системы представляют собой группу кристаллических структур в соответствии с осевой системой, используемой для описания их решетки. Каждая решетчатая система состоит из трех осей с определенным геометрическим расположением. Все кристаллы попадают в одну из семи систем решеток. Они похожи, но не совсем такие же, как семь кристаллических систем .
| Кристальная семья | Решетчатая система | Точечная группа ( обозначение Шенфлиса ) |
14 решеток Браве | |||
|---|---|---|---|---|---|---|
| Примитивный (P) | По центру основания (S) | По центру тела (I) | По центру лица (F) | |||
| Триклиник (а) | C i | 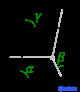
AP |
||||
| Моноклиника (м) | C 2 ч | 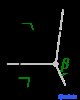
mP |
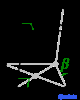
РС |
|||
| Орторомбический (о) | Д 2ч | 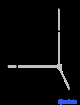
oP |
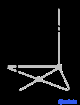
Операционные системы |
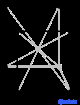
oI |

из |
|
| Тетрагональный (т) | Д 4ч | 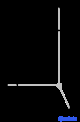
tP |
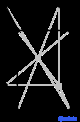
tI |
|||
| Шестиугольный (h) | Ромбоэдрический | D 3d | 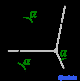
час |
|||
| Шестиугольный | Д 6ч | 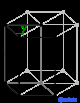
л.с. |
||||
| Кубический (c) | О ч | 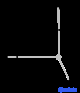
cP |
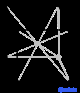
cI |
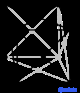
cF |
||
Самая простая и наиболее симметричная, кубическая или изометрическая система, имеет симметрию куба , то есть имеет четыре оси вращения третьего порядка , ориентированные под углом 109,5 ° ( тетраэдрический угол ) относительно друг друга. Эти тройные оси лежат по диагоналям тела куба. Остальные шесть решетчатых систем являются гексагональной , тетрагональной , ромбоэдрической (часто путают с тригональной кристаллической системой ), орторомбической , моноклинной и триклинной .
Решетки Браве , также называемые пространственными решетками , описывают геометрическое расположение узлов решетки и, следовательно, трансляционную симметрию кристалла. Три измерения пространства дают 14 различных решеток Браве, описывающих трансляционную симметрию. Все известные сегодня кристаллические материалы, за исключением квазикристаллов , вписываются в одну из этих схем. Четырнадцать трехмерных решеток, классифицированных по системе решеток, показаны выше.
Кристаллическая структура состоит из одной и той же группы атомов, основы , расположенной вокруг каждой точки решетки. Таким образом, эта группа атомов бесконечно повторяется в трех измерениях в соответствии с расположением одной из решеток Браве. Характерное вращение и зеркальная симметрия элементарной ячейки описываются ее кристаллографической точечной группой .
Кристаллическая система - это набор точечных групп, в которых сами точечные группы и соответствующие им пространственные группы назначены решеточной системе. Из 32 точечных групп, существующих в трех измерениях, большинство относятся только к одной системе решетки, и в этом случае кристаллическая система и система решетки имеют одно и то же имя. Однако пять точечных групп приписываются двум системам решеток, ромбоэдрической и гексагональной, поскольку обе системы решеток обладают тройной вращательной симметрией. Эти точечные группы относятся к тригональной кристаллической системе.
| Кристальная семья | Кристаллическая система | Группа точек / класс кристалла | Schönflies | Точечная симметрия | Заказ | Абстрактная группа |
|---|---|---|---|---|---|---|
| триклинический | педальный | C 1 | энантиоморфный полярный | 1 | банальный |
|
| пинакоидальный | C i (S 2 ) | центросимметричный | 2 | циклический |
||
| моноклинический | клиновидный | C 2 | энантиоморфный полярный | 2 | циклический |
|
| домический | C s (C 1h ) | полярный | 2 | циклический |
||
| призматический | C 2 ч | центросимметричный | 4 | Кляйн четыре |
||
| ромбический | ромбико-дисфеноидальный | D 2 (В) | энантиоморфный | 4 | Кляйн четыре |
|
| ромбовидно- пирамидальный | C 2v | полярный | 4 | Кляйн четыре |
||
| ромбовидно- дипирамидальный | Д 2 ч (В ч ) | центросимметричный | 8 | |||
| четырехугольный | тетрагонально-пирамидальный | C 4 | энантиоморфный полярный | 4 | циклический |
|
| тетрагонально-дисфеноидальный | S 4 | нецентросимметричный | 4 | циклический |
||
| тетрагонально-дипирамидальный | C 4ч | центросимметричный | 8 | |||
| тетрагонально-трапецоэдрический | D 4 | энантиоморфный | 8 | двугранный |
||
| дитетрагонально-пирамидальный | C 4v | полярный | 8 | двугранный |
||
| тетрагонально-скаленоэдрический | D 2d (V d ) | нецентросимметричный | 8 | двугранный |
||
| дитетрагонально-дипирамидальный | Д 4ч | центросимметричный | 16 | |||
| шестиугольный | тригональный | тригонально-пирамидальный | C 3 | энантиоморфный полярный | 3 | циклический |
| ромбоэдрический | C 3i (S 6 ) | центросимметричный | 6 | циклический |
||
| тригонально-трапецоэдрический | D 3 | энантиоморфный | 6 | двугранный |
||
| дитригонально-пирамидальный | C 3v | полярный | 6 | двугранный |
||
| дитригонально-чешуйчатый | D 3d | центросимметричный | 12 | двугранный |
||
| шестиугольный | гексагонально-пирамидальный | С 6 | энантиоморфный полярный | 6 | циклический |
|
| тригонально-дипирамидальный | C 3ч | нецентросимметричный | 6 | циклический |
||
| гексагонально-дипирамидальный | C 6h | центросимметричный | 12 | |||
| гексагонально-трапециевидный | D 6 | энантиоморфный | 12 | двугранный |
||
| дигексагонально-пирамидальный | C 6v | полярный | 12 | двугранный |
||
| дитригонально-дипирамидный | Д 3ч | нецентросимметричный | 12 | двугранный |
||
| дигексагонально-дипирамидальный | Д 6ч | центросимметричный | 24 | |||
| кубический | тетартоидный | Т | энантиоморфный | 12 | чередование |
|
| диплоидный | Т ч | центросимметричный | 24 | |||
| гироидный | О | энантиоморфный | 24 | симметричный |
||
| шестигранный | Т д | нецентросимметричный | 24 | симметричный |
||
| гексоктаэдрический | О ч | центросимметричный | 48 | |||
Всего существует семь кристаллических систем: триклинная, моноклинная, ромбическая, тетрагональная, тригональная, гексагональная и кубическая.
Кристаллографические точечная группа или кристаллический класс представляет собой математическую группу , включающую операции симметрии , которые оставляют по меньшей мере , одну точку неподвижным , и что оставить внешний вид кристаллической структуры без изменений. Об этом говорит сайт https://intellect.icu . Эти операции симметрии включают
Оси вращения (собственные и несобственные), плоскости отражения и центры симметрии вместе называются элементами симметрии . Всего существует 32 возможных класса кристаллов. Каждую из них можно отнести к одной из семи кристаллических систем.
Помимо операций точечной группы, пространственная группа кристаллической структуры содержит операции трансляционной симметрии. Это включает:
продолжение следует...
Часть 1 Кристаллическая структура и решетка, ее моделирование, Дефекты кристалла
Часть 2 Атомная координация - Кристаллическая структура и решетка, ее моделирование, Дефекты
Часть 3 Пузырьковая модель кристалла - Кристаллическая структура и решетка, ее моделирование,
Часть 4 - Кристаллическая структура и решетка, ее моделирование, Дефекты кристалла
Исследование, описанное в статье про кристаллическая структура, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое кристаллическая структура, кристаллическая решетка, дефекты кристалла и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Материаловедение и материалы электронных аппаратов
Комментарии
Оставить комментарий
Материаловедение и материалы электронных аппаратов
Термины: Материаловедение и материалы электронных аппаратов