Лекция
Привет, Вы узнаете о том , что такое 2.3. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ МЕТАЛЛИЧЕСКИХ ПРОВОДНИКОВ, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 2.3. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ МЕТАЛЛИЧЕСКИХ ПРОВОДНИКОВ , настоятельно рекомендую прочитать все из категории Материаловедение и материалы электронных аппаратов.
Из физики известно, что электроны обладают свойством корпускулярно-волнового дуализма. Поэтому движение электронов в металле можно рассматривать как распространение плоских волн, длина которых определяется соотношением де Бройля:
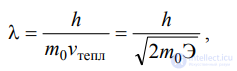
где m0 – масса электрона; vтепл – скорость теплового движения; h – постоянная Планка.
Так как в металлах концентрация электронного газа n практически не зависит от температуры, то зависимость удельной электропроводности σ от температуры полностью определяется температурной зависимостью подвижности µ носителей заряда – электронов вырожденного электронного газа. Об этом говорит сайт https://intellect.icu . В достаточно чистом металле концентрация примесей невелика и подвижность вплоть до весьма низких температур определяется рассеянием электронов на колебаниях решетки.
В области высоких температур подвижность электронов обратно пропорциональна T. Известно, что удельная электропроводность определяется выражением
σ = enµ .
Следовательно
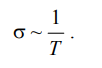
Удельное сопротивление
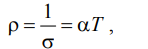
где α – температурный коэффициент сопротивления.
В области низких температур концентрация фононного газа пропорциональна T 3. Поэтому длина свободного пробега электронов, обусловленная рассеянием на фононах, должна быть обратно пропорциональна T 3:
L ~ T−3.
Однако это соотношение не учитывает того факта, что при низких температурах средний импульс фононов оказывается настолько небольшим по сравнению с импульсом электронов проводимости, что для уничтожения движения электрона в данном направлении требуется не один, а ν ~ T 2 актов рассеяния его на фононах. Поэтому эффективная длина свободного пробега электрона Lэф, на протяжении которой происходит хаотизация его движения, равна
Lэф ~ T−5 .
Следовательно σ ~ T−5 и ρ ~ T5 .
Данная статья про 2.3. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ МЕТАЛЛИЧЕСКИХ ПРОВОДНИКОВ подтверждают значимость применения современных методик для изучения данных проблем. Надеюсь, что теперь ты понял что такое 2.3. ТЕМПЕРАТУРНАЯ ЗАВИСИМОСТЬ УДЕЛЬНОГО СОПРОТИВЛЕНИЯ МЕТАЛЛИЧЕСКИХ ПРОВОДНИКОВ и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Материаловедение и материалы электронных аппаратов
Из статьи мы узнали кратко, но содержательно про
Комментарии
Оставить комментарий
Материаловедение и материалы электронных аппаратов
Термины: Материаловедение и материалы электронных аппаратов