Дискриминантный анализ - Конструирование психодиагностических тестов: традиционные математические модели и

Это продолжение увлекательной статьи про конструирование психодиагностических тестов.

...

дисциплинах, интеллекта, методик для профотбора и профориентации, тестов общих и специальных способностей и т. п. Внешний критерий может быть представлен номинальным, ранговым или количественным показателем, «привязанным» к объектам анализируемой ТЭД. Этот показатель в дальнейшем будет обозначаться z. Специфика z влияет на выбор метода определения параметров диагностической модели.

Регрессионный анализ

С позиции регрессионного анализа критериальный показатель z рассматривается как «зависимая» переменная (как правило, ранговая или количественная), которая выражается функцией от «независимых» признаков xi,...,xp. Для оценки эффективности регрессионной диагностической модели вводится вектор остатков ε=(ε1,...,εn)', который отражает влияние на z совокупности неучтенных случайных факторов либо меру достижимой аппроксимации значений критериального показателя zi функциями типа у(хi). Линейная функция регрессии записывается следующим образом

zi = wo + w'xi + εi

w0 называется свободным членом, а элементы весового вектора w=(w1 ..., wр) называются коэффициентами регрессии.

Различают два подхода в зависимости от происхождения матрицы данных. В первом считается, что признаки xjявляются детерминированными и случайной величиной является только зависимая переменная (критериальный показатель) z. Эта модель используется наиболее часто и называется моделью с фиксированной матрицей данных. Во втором подходе считается, что признаки x1, ..., xр и z — случайные величины, имеющие совместное распределение. В такой ситуации оценка уравнения регрессии есть оценка условного математического ожидания случайной величины z в зависимости от случайных величин xi,..., xp /Андерсон Т., 1963/. Данная модель называется моделью со случайной матрицей данных /Енюков И. С., 1986/. Каждый из приведенных подходов имеет свои особенности. В то же время показано, что модели с фиксированной матрицей данных и со случайной матрицей данных отличаются только статистическими свойствами оценок параметров уравнения регрессии, тогда как вычислительные аспекты этих моделей совпадают /Демиденко Е. 3., 1981/. В уравнении линейной функции регрессии обычно полагают, что величины εi(i=1,N) независимы и случайно распределены с нулевым средним и дисперсией σ2ε, а оценка параметров w0 и w производится с помощью метода наименьших квадратов (МНК). Ищется минимум суммы квадратов невязок

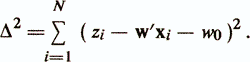
Это приводит к нормальной системе линейных уравнений:

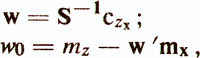
где czx — вектор оценок ковариации между критериальным по­казателем z и признаками х1, ..., xp; mz — оценка среднего значения z; mx и S — вектор средних значений и матрица ковариации признаков xi, ..., xp. Основные показатели качества регрессионной диагностической модели следующие /Енюков И. С., 1986/: — остаточная сумма квадратов

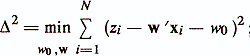
— несмещенная оценка дисперсии ошибки

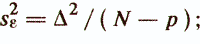
— оценка дисперсии прогнозируемой переменной

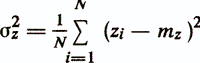
— коэффициент детерминации

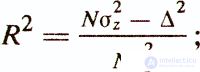
— оценка дисперсии коэффициентов регрессии

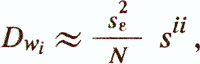
где sii — соответствующий элемент S-1;

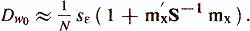
Особого внимания заслуживает приведенный выше коэффициент детерминации R2. Он представляет собой квадрат коэффициента корреляции между значениями критериальной переменной z и значениями, рассчитываемыми с помощью модели у(х)=w'x+w0 (квадрат коэффициента множественной корреляции). Статистический смысл коэффициента детерминации заключается в том, что он показывает, какая доля зависимой переменной z объясняется построенной функцией регрессии у(х). Например, при коэффициенте детерминации 0,49 регрессионная модель объясняет 49% дисперсии критериального показателя, остальные же 51% считаются обусловленными факторами, не отраженными в модели.

Еще одним важным показателем качества регрессионной модели является статистика

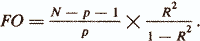
С помощью этой статистики проверяется гипотеза Н0: w1=w2= =...=wp=0, то есть гипотеза о том, что совокупность признаков xi,...,xp не улучшает описания критериального показателя по сравнению с тривиальным описанием zi=mz. Если FO>fp,N-p-1, где fp,N-p-1 — случайная величина, имеющая F-pacпределение c р и N-p-l степенями свободы, то Н0 отклоняется (критерий Фишера).

В регрессионном анализе нередко проверяется другая гипотеза о равенстве нулю каждого из коэффициентов регрессии в отдельности Н0: wi=0. Для этого вычисляется Р-значение Р ( |tN-р| > ti}, где ti = wi/√Dwi, а величина tN-p имеет t-распределение с (N-р) степенями свободы. Здесь следует подчеркнуть, что принятие Hо (высокое Р-значение) еще не говорит о том, что рассматриваемый признак xi нужно исключить из модели. Этого делать нельзя, поскольку суждение о ценности данного признака может выноситься, исходя из анализа совокупного взаимодействия в модели всех признаков. Поэтому высокое p-значение служит только «сигналом» о возможной неинформативности того или иного признака.

Описанная выше технология оценки параметров линейной диагностической модели относится к одной из классических схем проведения регрессионного анализа. Известно большое количество других вариантов такого анализа, опирающихся на различные допущения о структуре экспериментальных данных и свойствах линейной модели (например, Демиденко Е. 3., 1982; Дрейпер Н. и др., 1973; Мостеллер Ф. и др., 1982). Однако в практике конструирования психодиагностических тестов применение классических схем регрессионного анализа с развитым математическим аппаратом оценки параметров регрессионной модели часто вызывает большие сложности. Причин указанных сложностей немного, но они весьма весомы.

Во-первых, сюда относится специфический характер исходных психодиагностических признаков и критериального показателя, которые, как правило, измеряются в дихотомических и ординальных шкалах. Меры связи таких признаков, как указывалось выше, имеют несколько отличную от коэффициента корреляции количественных признаков трактовку и сравнительно трудно сопоставимое поведение внутри интервала [0,1]. Поэтому расчетные формулы регрессионного анализа, полученные для количественных переменных, приобретают значительную степень приблизительности.

Во-вторых, число исходных признаков, подвергающихся эмпирико-статистическому анализу в психодиагностических исследованиях, велико (может достигать несколько сотен) и между ними, как правило, встречаются объемные группы сильно связанных признаков. В этих условиях возникает явление мультиколлинеарности, приводящее к плохой обусловленности и в предельном случае вырожденности матрицы ковариации S. При плохой обусловленности S решение системы является неустойчивым — норма вектора оценок коэффициентов регрессии и отдельные компоненты w могут стать весьма большими, в то время как, например, знаки коэффициентов wi могут инвертироваться при малом изменении исходных данных /Демиденко Е. 3., 1982; Айвазян С. А. и др., 1985/.

Указанные обстоятельства, ряд которых можно продолжить, обусловили приоритет в психодиагностике «грубых» методов построения регрессионных моделей. В основном проблема оценки параметров линейной психодиагностической модели сведена к задаче отбора существенных признаков.

Известно много подходов к решению задачи определения группы информативных признаков: рассмотрение всех возможных комбинаций признаков; метод «k» лучших признаков /Барабаш Б. А., 1964; Загоруйко Н. Г., 1964/; методы последовательного уменьшения и увеличения группы признаков /Marill T. et al., 1963/; обобщенный алгоритм «плюс l минус r» /Kittrer J., 1978/; методы, основанные на стратегии максмина /Backer E. et al., 1911/; эволюционные алгоритмы, в частности, алгоритмы случайного поиска с адаптацией /Лбов Г. С., 1965/; метод ветвей и границ /Narendra P. M. et al., 1976/ и другие.

Значительные вычислительные трудности, связанные с высокой размерностью пространства исходных признаков, привели к тому, что в практике конструирования психодиагностических тестов применяются наиболее простые алгоритмы определения состава линейной регрессионной модели.

1) Метод «k» лучших признаков.

В основе этого метода лежит предположение о статистической независимости анализируемых признаков. Если в качестве критерия эффективности линейной диагностической модели используется коэффициент детерминации R2, то мерой информативности отдельно взятого признака может служить его коэффициент корреляции с критериальным показателем r(xi, z) (в зависимости от типа исходных признаков и от шкалы, в которой измерен критериальный показатель, используются соответствующие меры связи). Исходное множество признаков xi....,xpупорядочивается по модулю коэффициента корреляции

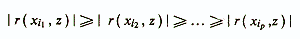
и из построенного ряда отбирается «k» первых, наиболее ценных признаков.

Чем строже соблюдается условие независимости отбираемых признаков, тем лучше получается конечный результат. В /Общая психодиагностика..., 1987/ приводится следующая иллюстрация X. Гаррета эффективности алгоритма, позволяющего подобрать оптимальный набор пунктов теста. Пусть имеется 20 пунктов, каждый из которых имеет корреляцию с внешним критерием порядка 0,30. Если эти пункты коррелируют друг с другом на уровне r(xi,xj)=0,60, то множественный коэффициент корреляции линейной диагностической модели равняется 0,38, если же r(xi,xj)=0,30, множественная корреляция повышается до 0,52. Наконец, при r(xi,xj)=0,10 эффективность теста достигает высокого значения 0,79. Этот факт хорошо исследован в теории регрессионного анализа (например, Хей Дж., 1987). Он также достаточно понятен на качественном уровне рассуждений, так как сильная зависимость признаков означает дублирование большой части информации о проявлении диагностируемого свойства у исследуемых объектов. пользуют более сложные методы анализа экспериментальной информации.

2) Методы последовательного увеличения и уменьшения группы признаков (ПУВГ) и (ПУМГ).

В зависимости от критерия оптимальности группы признаков возможны различные варианты алгоритма ПУВГ. Чаще всего применяется вариант, основанный на анализе частных корреляций между внешним критерием и пунктами теста. Алгоритм ПУВГ выглядит следующим образом.

Шаг 1. Из набора исходных признаков xi,...,xp выбирается переменная xi1, имеющая максимальное значение квадрата коэффициента парной корреляции с критериальным показателем r2(xi1,z). Признак xi1 составляет начальный набор диагностических переменных Х(1).

Шаг 2. Пусть уже построен информативный набор из j признаков X(j)=xi1, ... , xij. Ищется признак xij+1 из условия

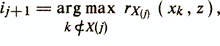
где rХ(j)(xk,z) — частный коэффициент корреляции между xk и z при фиксированных значениях переменных из Х(j). При этом дополнительно проверяется условие линейной независимости признака xk от набора признаков Х(j), которое обеспечивает вычислительную устойчивость алгоритма,

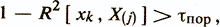
где R2[xk, X(j)] — квадрат коэффициента множественной корреляции набора X(j) с проверяемым признаком хk

τпор — заданная малая положительная величина. После определения переменной xij+1 проверяются условия остановки алгоритма ПУВГ. Возможно одно из следующих условий остановки /Енюков И. С., 1986/.

— Достигнуто заданное количество признаков р3, то есть j+1=p3. — Проверяется гипотеза о равенстве нулю максимального по абсолютной' величине коэффициента частной корреляции из р—j коэффициентов частной корреляции признаков, не входящих в X(j). Если эта гипотеза подтверждается, то набор признаков считается окончательным.

— Достигнуто максимальное значение FО-статистики для оценки качества регрессионного уравнения, которое определяется по формуле расчета FО. Если ни одно из условий не выполняется, то признак xij+1, присоединяется к набору Х(j) и происходит возвращение к шагу 2. После остановки алгоритма каждому из признаков, вошедших в информативную группу, могут быть присвоены веса, выражающие вклад каждого признака в критерий, не сводимый к вкладу других признаков /Аванесов В. С., 1982/.

Несмотря на более изощренные операции с экспериментальной информацией по сравнению с методом «k» лучших признаков, метод ПУВГ является во многом эвристичным. Он не гарантирует получения оптимального результата, который может быть достигнут с помощью полного перебора всех возможных комбинаций исходных признаков. Отклонение от оптимального решения вероятно уже на первом шаге работы алгоритма ПУВГ, когда выбирается начальный диагностический признак из информативной группы. Хотя этот признак имеет максимальную корреляцию с критериальным показателем, это вовсе не означает, что он обязательно вошел бы в группу информативных признаков, если бы начальным был выбран какой-либо другой признак.

Не гарантирует получения оптимального результата и метод последовательного уменьшения группы признаков ПУМГ, в котором начальное уравнение регрессии строится для полного набора исходных признаков. Из этого полного уравнения затем последовательно удаляется по одной переменной и для оставшихся признаков подсчитывается значение коэффициента детерминации R2 или какого-либо иного интегрального показателя качества функции регрессии. Алгоритм ПУМГ останавливается, когда дальнейшее упрощение уравнения регрессии начинает ухудшать его качество. С помощью указанного алгоритма могут быть получены более эффективные результаты, чем для ПУВГ, в случае сравнительно небольшого объема группы исходных признаков. Для высоких размерностей пространства исходных признаков (а при конструировании психодиагностических тестов размерность достигает десятков и даже сотен) возникают серьезные проблемы оценки показателя качества регрессионного уравнения, так как влияние отдельно взятого признака на суммарный эффект диагностической модели становится сопоставимым с погрешностью его измерения.

Обобщением ПУВГ и ПУМГ служит метод «плюс l минус r», который, как следует из его названия, поочередно работает то на добавление, то на исключение признаков в уравнение регрессии. В целом можно отметить, что все упомянутые методы определения состава признаков в уравнении регрессии содержат в той или иной мере эвристическую составляющую. В каждом конкретном случае трудно заранее предугадать, какой из этих методов приведет к результатам, более близким к оптимальным. Поэтому на практике попытки приблизиться к желаемому оптимуму всегда сопряжены с комбинированным применением различных алгоритмов поиска группы информативных признаков в диагностической регрессионной модели.

Дискриминантный анализ

Если критериальный показатель z измерен в номинальной шкале или связь этого показателя с исходными признаками является нелинейной и носит неизвестный характер, для определения параметров диагностической модели используются методы дискриминантного анализа. В этом случае испытуемые, результаты обследования которых представлены в ТЭД, в соответствии с внешним критерием разбиваются на группы (классы), а эффективность диагностической модели рассматривается под углом зрения ее способности разделять (дискриминировать) диагностируемые классы.

Большая группа методов дискриминантного анализа в той или иной мере основана на байесовской схеме принятия решения о принадлежности объектов диагностическим классам. Байесовский подход базируется на предположении, что задача сформулирована в терминах теории вероятностей и известны все представляющие интерес величины: априорные вероятности P(ωi) для классов ωi(i=1,K) и условные плотности распределения значений вектора признаков Р(х/ωi). Правило Байеса заключается в нахождении апостериорной вероятности Р(ωi/х), которая вычисляется следующим образом

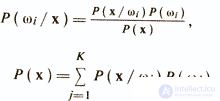
Решение о принадлежности объекта хk к классу ωj принимается при выполнении условия, обеспечивающего минимум средней вероятности ошибки классификации.

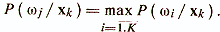
Если рассматриваются два диагностических класса ω1 и ω2, то в соответствии с этим правилом принимается решение ω1 при Р (ω1/х )>Р( ω2/х) и ω2 при P(ω2/x)>Р(ω1/x). Величину Р(ωi/х) в правиле Байеса часто называют правдоподобием ωi при данном х и принятие решения осуществляется через отношение правдоподобия или через его логарифм

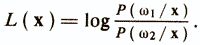
Для дихотомических признаков, с которыми во многих случаях приходится иметь дело при конструировании психодиагностических тестов, р-мерный вектор признаков х может принимать одно из n=2р дискретных значений v1,...,vn. Функция плотности Р(х/ωi) становится сингулярной и заменяется на Р(vk/ωi) — условную вероятность того, что х=vk при условии класса ωi.

На практике в дискретном случае, как и в непрерывном, когда число исходных признаков xi велико, определение условных вероятностей встречает значительные трудности и зачастую не может быть осуществлено. Это связано, с одной стороны, с нереальностью даже простого просмотра всех точек дискретного пространства дихотомических признаков. Так, например, если использовать в качестве исходных признаков для построения диагностического правила утверждения тест-опросника MMPI, то р=550 и тем самым n=2550. С другой стороны, даже при гораздо меньшем количестве признаков для достоверной оценки условных вероятностей необходимо иметь результаты обследования весьма большого количества испытуемых.

Распространенным приемом преодоления указанных трудностей служит модель, в основе которой лежит допущение о независимости исходных дихотомических признаков. Пусть для определенности компоненты вектора х принимают значения 1 либо 0. Обозначим pi=Р(xi=1/ωi) — вероятность того, что признак xi равен 1 при условии извлечения объектов из диагностического класса ω1, и qi=Р(xi=1/(ω2) — вероятность равенства 1 признака xi в классе ω2. В случае pi>qi следует ожидать, что z-й признак будет чаще принимать значение 1 в классе ω1, нежели в ω2. В предположении о независимости признаков можно представить Р(х/ωi) в виде произведения вероятностей

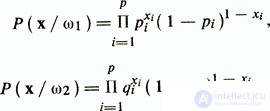
Логарифм отношения правдоподобия в этом случае определяется следующим образом

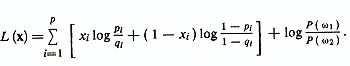
Видно, что данное уравнение линейно относительно признаков xi. Поэтому можно записать

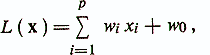
где весовые коэффициенты 

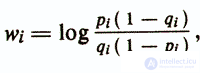
а величина порога 

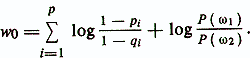
Если L(xk)>0, то принимается решение о принадлежности объекта хk к диагностическому классу ω1, а если L(xk)<0, то ω2.

Приведенный результат аналогичен рассмотренным выше схемам лцнейного регрессионного анализа для независимых признаков. Можно выразить значения рi и qi с помощью обозначений, принятых для элементов таблицы сопряженности дихотомических признаков (см. табл. 2) Здесь в качестве одного из двух дихотомических признаков будет выступать индекс диагностического класса ωi. Подставив эти обозначения в логарифм, получим wi=log(bc/ad). To есть выражение для вычисления весовых коэффициентов в байесовской решающей функции для независимых признаков дает значения wi, монотонно связанные с коэффициентом Пирсона φ, который в ряде случаев может использоваться при определении коэффициентов уравнения линейной регрессии.

Результаты дискриминантного и регрессионного анализа для случая двух классов во многом совпадают. Различия проистекают в основном из-за применения разных критериев эффективности диагностической модели. Если интегральным показателем качества регрессионного уравнения служит квадрат коэффициента множественной корреляции с внешним критерием, то в дискриминантном анализе этот показатель, как правило, сформулирован относительно вероятности ошибочной классификации (ВОК) исследуемых объектов. В свою очередь, для вскрытия взаимосвязи ВОК со структурой экспериментальных данных в дискриминантном анализе широко используются геометрические представления о разделении диагностируемых классов в пространстве признаков. Воспользуемся этими представлениями для описания других, отличных от байесовского, подходов дискриминантного анализа.

Совокупность объектов, относящихся к одному классу ωi, образует «облако» в р-мерном пространстве Rp, задаваемом исходными признаками. Для успешной классификации необходимо, чтобы /Енюков И. С., 1986/:

а) облако из ωi в основном было сконцентрировано в некоторой области Di пространства Rp;

б) в область Di попала незначительная часть «облаков» объектов, соответствующих остальным классам.

Построение решающего правила можно рассматривать как задачу поиска К непересекающихся областей Di(i=l,K), удовлетворяющих условиям а) и б). Дискриминантные функции (ДФ) дают определение этих областей путем задания их границ в многомерном пространстве Rp. Если объект х попадает в область Di, то будем считать, что принимается решение о принадлежности объекта к ωi. Обозначим Р (ωi/ωj) — вероятность того, что объект из класса ωj ошибочно попадает в область Di, соответствующую классу ωi. Тогда критерием правильного определения областей А будет

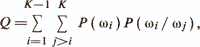
где Р(ωi — априорная вероятность появления объекта из ωi. Критерий Q называется критерием средней вероятности ошибочной классификации. Минимум Q достигается при использовании, в частности, рассмотренного выше байесовского подхода, который, однако, может быть практически реализован только при справедливости очень сильного допущения о независимости исходных признаков и в этом случае дает оптимальную линейную диагностическую модель. Большое количество других подходов также использует линейные дискриминантные функции, но при этом на структуру данных накладываются менее жесткие ограничения. Рассмотрим основные из этих подходов.

Для случая двух классов ω1 и ω2 методы построения линейной дискриминантной функции (ЛДФ) опираются на два предположения. Первое состоит в том, что области D1 и D2, в которых концентрируются объекты из диагностируемых классов ω1 и ω2, могут быть разделены (р-1)-мерной гиперплоскостью у(х)+wo=w1x1+w2x2+...+wpxp+w0=0. Коэффициенты wi в данном случае интерпретируются как параметры, характеризующие наклон гиперплоскости к координатным осям, a wo называется порогом и соответствует расстоянию от ги­перплоскости до начала координат. Преимущественное расположение объектов одного класса, например ω1, по одну сторону гиперплоскости выражается в том, что для них, большей частью, будет выполняться условие у(х)<0, а для объектов другого класса ω2 — обратное условие у(х)>0. Второе предположение касается критерия качества разделения областей D1 и D2 гиперплоскостью у(х)+wo=0. Наиболее часто предполагается, что разделение будет тем лучше, чем дальше отстоят друг от друга средние значения случайных величин m1=Е{у(х)}, хєω1 и m2=Е{у(х)},хєω2 где Е{ •} — оператор усреднения.

В простейшем случае полагают, что классы ω1 и ω2 имеют одинаковые ковариационные матрицы S1=S2=S. Тогда вектор оптимальных весовых коэффициентов w определяется следующим образом /Андерсон Т., 1963/

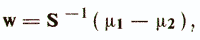
где μi — вектор средних значений признаков для класса ωi. Весовые коэффициенты обеспечивают максимум критерия

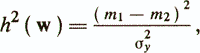
где σ2у — дисперсия у(х), полагаемая одинаковой для обоих классов. Максимальное значение h2(w) носит название расстояния Махаланобиса между классами ω1 и ω2 и равно

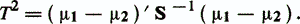
Для определения величины порога wo вводят предположение о виде законов распределения объектов. Если объекты каждого класса имеют многомерное нормальное распределение с одинаковой ковариационной матрицейS и векторами средних значений μi, то пороговое значение wo, минимизирующее критерий Q, будет

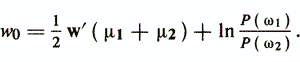
Верно следующее утверждение об оптимальности ЛДФ: если объекты из ωi(i=l,2) распределены согласно многомерному нормальному закону с одинаковой ковариационной матрицей, то решающее правило w'x>w0, параметры которого определены, является наилучшим в смысле критерия средней вероятности ошибочной классификации.

Для случая, когда число классов больше двух (К>2), обычно определяется К дискриминантных весовых векторов (направлений) 

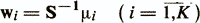
и пороговые величины

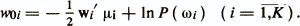
Объект х относится к классу ωi, если выполняется условие

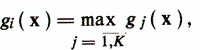
где gj(x) = wj'/x—woj.

В формулы вычисления пороговых значений wo и woi входят величины априорных вероятностей Р(ωi). Априорная вероятность Р(ωi) соответствует доле объектов, относящихся к классу ωi в большой серии наблюдений, проводящейся в некоторых стационарных условиях. Обычно Р(ωi) неизвестны. Поэтому при решении практических задач, не меняя дискриминантных весовых векторов, эти значения задаются на основании субъективных оценок исследователя. Также нередко полагают эти значения равными или пропорциональными объемам обучающих выборок из рассматриваемых диагностических классов. Другой подход к определению параметров линейных дискриминантных функций использует в качестве критерия соотношение внутриклассовой дисперсии проекций объектов на направление у(х)=w'x с общей дисперсией проекций объединенной выборки. Обычно используются те же предположения, что и в предыдущем случае. А именно, классы ωi(i=l,K) представлены совокупностями нормально распределенных в р-мерном пространстве объектов с одинаковыми ковариационными матрицами S и векторами средних значений μi. Обозначим С — ковариационную матрицу объединенной совокупности объектов объема 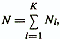, a μ0 — вектор средних значений этой совокупности. Выражение С через S и дается следующей формулой:

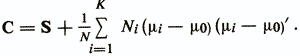
Дисперсия проекций всей совокупности объектов на направление у(х) составит c2у=w'Cw, а внутриклассовая дисперсия будет S2y=w'Sw. Таким образом, критерий оптимальности выбранного направления у(х) для разделения классов ωi запишется в следующем виде:

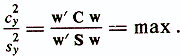
Это отношение показывает, во сколько раз суммарная дисперсия, которая обусловлена как внутриклассовым разбросом, так и различиями между классами, больше дисперсии, обусловленной только внутриклассовым разбросом. Весовой вектор w, удовлетворяющий данному уравнению, исходя из рассмотренной ранее геометрической интерпретации линейной диагностической модели, задает новую координатную ось в р-мерном пространстве y(x)=w'x (||w||=1) с максимальной неоднородностью исследуемой совокупности объектов. Новой переменной у(х)=w'x соответствует, no-существу, первая главная компонента объединенной совокупности объектов, полученная с учетом дополнительной обучающей информации о принадлежности объектов диагностическим классам ωi. Весовой вектор w, при котором достигается максимальное значение критерия оптимальности выбранного направления, определяется в результате решения обобщенной задачи на собственные значения

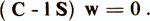
Всего существует р собственных векторов, удовлетворяющих приведенному уравнению. Эти векторы упорядочивают по величине собственных чисел l1>l2>...>lp и получают систему ортогональных канонических направлений w1, ..., wp.

Минимальное значение отношения 

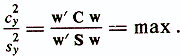
равно 1 и означает, что для выбранного направления w весь имеющийся разброс переменной у(х) объясняется только внутриклассовым разбросом и не несет никакой информации о различии между классами ωi. Для случая К=2 оценка весового дискриминантного вектора wF=S-1(μ1-μ2) является собственным вектором для (C-1S)w=0 с собственным числом lF=T2+1. Любой вектор, ортогональный wF, будет также решением (C-1S)w=0 с собственным значением равным единице. Поэтому для ответа на вопрос, какое число n<р канонических направлений необходимо учесть при К>2, чтобы не потерять информацию о межклассовых различиях,

продолжение следует...

Продолжение:

Часть 1 Конструирование психодиагностических тестов: традиционные математические модели и алгоритмы
Часть 2 2. Методы, основанные на критерии автоинформативности системы признаков - Конструирование
Часть 3 Дискриминантный анализ - Конструирование психодиагностических тестов: традиционные математические модели и
Часть 4 Типологический подход - Конструирование психодиагностических тестов: традиционные математические модели и
Часть 5 - Конструирование психодиагностических тестов: традиционные математические модели и алгоритмы
Часть 6 - Конструирование психодиагностических тестов: традиционные математические модели и алгоритмы