2. Методы, основанные на критерии автоинформативности системы признаков - Конструирование

Это продолжение увлекательной статьи про конструирование психодиагностических тестов.

...

/> 3) Расстояние Махаланобиса -

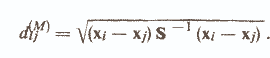
де S — ковариационная матрица генеральной совокупности, из соторой извлечены объекты хi и хj
. Ее элементы вычисляются по формуле Ski(см. выше). Эта мера применяется при сильной зависимости и неоднородности исследуемых признаков, так как она инвариантна к линейным преобразованиям пространства признаков (изменению масштаба и повороту осей).

4) Расстояние Минковского —

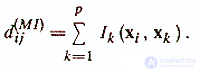
Это расстояние еще называют «городской метрикой», поскольку в данном случае расстояние между точками определяется аналогично расстоянию вдоль взаимно перпендикулярных улиц городских кварталов /Александров В. В. и др., 1990/. Городская метрика применяется для измерения расстояния между объектами, описанными ординальными признаками. Ik(хi, хj
) равно разнице номеров градаций по k-му признаку у сравниваемых объектов хi и хj
.

5) Расстояние Хэмминга -

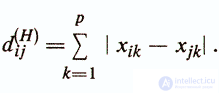
Данная мера наиболее часто используется для определения различий между объектами, задаваемыми дихотомическими признаками и интерпретируется как число несовпадений значений признаков у рассматриваемых объектов хi и хj
. Для дихотомических признаков она соответствует квадрату евклидова расстояния. Так же как и для евклидова расстояния, может применяться взвешенное расстояние Хэмминга.

6) Другие меры близости для дихотомических признаков.

Эти меры близости обычно основаны на подсчете числа нулевых или единичных компонент признаков, совпавших или несовпавших на объектах хi и хj
, и придании этому числу различной степени важности. Подробно указанные меры рассматриваются в /Боннер Р. Е., 1969; Житков Г. Н., 1970; Елисеева И. И. и др., 1977/.

Представление информации о структуре экспериментальных данных посредством матриц связей признаков S и близостей (удаленностей) объектов D служит промежуточным звеном в процессе построения диагностических моделей у = у(х) различного типа. Независимо от этого типа различают две основные стратегии определения параметров диагностических моделей. Первая стратегия использует методы, опирающиеся непосредственно только на особенности конфигурации образовавшейся структуры экспериментальных данных, находящей свое выражение в числовых отношениях сходства и различия элементов ТЭД. Поэтому она называется стратегией, основанной на критерии автоинформа тивности экспериментальных данных. Например, если в матрице связей S обнаруживается группа сильно коррелирующих признаков, то, возможно, это является следствием отражения признаками, вошедшими в группу, эмпирического фактора, соответствующего требуемому диагностическому конструкту. Или, например, если, исходя из анализа компонент матрицы расстояний D, удается установить, что распределение объектов в пространстве признаков состоит из нескольких геометрических группировок, то это может быть основанием для попытки объяснить данный факт различиями изучаемых объектов по тестируемому свойству и построить адекватный диагностический алгоритм.

В то же время нужно хорошо представлять, что выявляемые группировки объектов в большой степени зависят от типа используемой меры расстояния между объектами и от используемой системы признаков. Так, в частности, «хорошая» с точки зрения решаемой диагностической задачи геометрическая структура распределения объектов в каком-либо подпространстве признаков может быть «развалена» добавлением к этому подпространству «шумящих» признаков или «подавлена» более «сильной» структурой, отражающей иррелевантный тестируемому свойству фактор. В свою очередь, значимые связи между признаками могут образовываться за счет расслоения выборки объектов под действием постороннего фактора. И, наоборот, отсутствие корреляций может объясняться влиянием неучтенной характеристики выборки (например, для лиц разного пола корреляции каких-либо признаков могут быть высокими, но иметь противоположные знаки. Поэтому в смешанной выборке корреляции этих же признаков будут близки к нулю).

Приведенные примеры, а также другие примеры, рассматриваемые в последующих разделах, показывают, что нередко для построения диагностической модели требуется привлечение дополнительной информации, кроме той, которая непосредственно содержится в исходной ТЭД. Эту дополнительную информацию называют обучающей, и ее несут сведения об эмпирических отношениях между объектами исследования, полученные тем или иным способом. Обучающая информация формируется по так называемым критериям внешней информативности или, иными словами, внешним критериям. Данная информация представляется в различных формах. Это может быть привязка к объектам значений «зависимой» переменной, измеренной в количественной шкале, номер однородного по тестируемому свойству класса, порядковый номер (ранг) объекта хi >
в ряду всех объектов, упорядоченных по степени проявления диагностируемого свойства, и, наконец, совокупности значений набора внешних (не включенных в анализируемую ТЭД) признаков, характеризующих тестируемый психологический феномен. При использовании обучающей информации объекты в исходном пространстве признаков в соответствии с внешним критерием как бы «окрашиваются в разнообразные цвета», что позволяет более целенаправленно находить способы преобразования исходных признаков в результирующий диагностический показатель. Методы, основанные на применении внешних критериев, составляют вторую стратегию определения параметров диагностических моделей.

В зависимости от совпадения критериев автоинформативности с критериями внешней информативности методы первой и второй стратегии могут приводить к сходным результатам. В то же время эти результаты в значительной мере зависят от того, с помощью каких преобразований раскрывается информационный потенциал исходных экспериментальных данных. Не существует диагностической «информативности вообще». Информативность данных существует только по отношению к применяемому типу диагностической модели, выбор которой, в свою очередь, определяется техническими ресурсами и теоретическими представлениями конкретных исследователей.

В психодиагностике превалируют линейные модели, в которых результирующий показатель представляется в виде взвешенной суммы исходных признаков

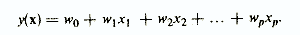
Распространенность линейных моделей объясняется прежде всего их наибольшей простотой, понятностью и «удоборешаемостью», позволяющей, в частности, вручную обрабатывать результаты тестирования. Например, лаборант, участвующий в психодиагностическом эксперименте, сравнивает ответы испытуемого на вопросы теста со специальным «ключом», суммирует совпадения с определенными весами и тем самым реализует линейную диагностическую модель.

С математической точки зрения развитие диагностики происходит в направлении отказа от линейных моделей /Айвазян С. А. и др., 1989/. Но, несомненно, они всегда будут иметь большое прикладное значение благодаря лаконичности и хорошей интерпретируемости.

Линейные модели удобны для рассмотрения геометрических иллюстраций вычисления результирующего показателя. Уравнение у(х)=0 — это уравнение гиперплоскости в пространстве признаков (рис.), а расстояние от объекта хi , который отображается точкой в данном пространстве, до гиперплоскости равно 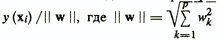 — норма весового вектора w.

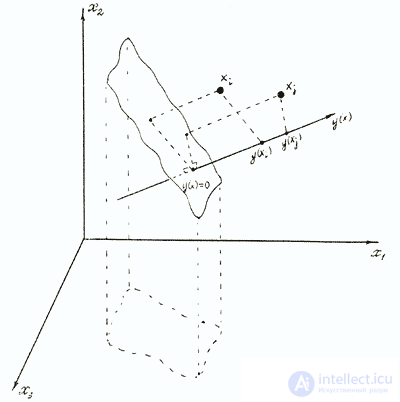
На рис. изображены два объекта хi и хj и кусок плоскости у(х) = 0 в трехмерном пространстве. Так как в данном случае норма весового вектора выбрана произвольно и равна 1, расстояния от хi и хj до плоскости непосредственно соответствуют значениям у(хi) и у(хj). Указанные значения часто бывает удобно интерпретировать как проекции хi и хj
на любую прямую в рассматриваемом пространстве признаков, перпендикулярную плоскости у(х)=0 Эта прямая обозначена на рисунке у(х).

Точка ее пересечения с плоскостью дает значение нуля на прямой. В дальнейшем будут неоднократно использоваться подобные геометрические иллюстрации. Это будет уместно и тогда, когда норма весового вектора не равна единице, так как искажение масштаба, которое наблюдается в данном случае, не повлечет за собой искажения главного — взаимного расположения проекций точек на прямую.

Рис. Иллюстрация линейной диагностической пространстве признаков модели в трехмерном пространстве признаков.

В зависимости от угла зрения, под которым рассматривается линейная диагностическая модель, она может иметь различные названия. Если, например, «у» трактуется как «зависимая» переменная, для которой ищется функциональная связь с «независимыми» переменными (признаками) xi, то уравнение линейной модели у(х) называется линейной функцией регрессии или уравнением множественной регрессии. Если рассматривается задача классификации объектов, то у=у(х) обычно называют линейной решающей функцией, а уравнение у(х)=0 — разделяющей границей или уравнением разделяющей гиперплоскости. Ниже при обсуждении того или иного метода определения параметров линейной диагностической модели тоже будут использоваться различные термины, но, как указывалось выше, глобальным атрибутом для разграничения этих методов является привлечение или не привлечение критерия внешней информативности.

 

2. Методы, основанные на критерии автоинформативности системы признаков

Формальные алгоритмы рассматриваемой группы методов непосредственно не оперируют обучающей информацией о требуемом значении диагностируемой переменной. В то же время эта информация в неявном виде всегда присутствует в экспериментальных данных. Она закладывается на самом первом этапе конструирования психодиагностического теста, когда экспериментатор формирует исходное множество признаков, каждый из которых, по его мнению, должен отражать определенные аспекты тестируемого свойства. При этом под отражением данного свойства отдельным признаком, как правило, понимается самый простой вид связи признака с диагностируемым показателем — корреляция xi с у. Если тестируемое свойство гомогенно, то имеются все основания полагать, что мерой информативности для окончательного отбора признаков может служить степень согласованного действия этих признаков в нужном направлении.

Внутренняя согласованность заданий теста является важной категорией методов, опирающихся на критерий автоинформативности системы признаков. Согласованность измеряемых реакций испытуемых на тестовые стимулы означает то, что они должны иметь статистическую направленность на выражение общей, главной тенденции теста. Геометрическая структура экспериментальных данных, сформированных под влиянием кумулятивного эффекта согласованного взаимодействия признаков, в несколько идеализированном варианте выглядит как облако точек в пространстве признаков, вписывающееся в гиперэллипсоид. Все пары признаков при такой структуре имеют статистически значимые корреляции, а уравнение главной оси гиперэллипсоида — есть линейная диагностическая модель тестируемого свойства.

На приведенных представлениях базируются практически все методы построения психодиагностических тестов, опирающиеся на критерий автоинформативности системы признаков и использующие категорию внутренней согласованности заданий теста. Ниже будут рассмотрены основные методы этой группы.

Метод главных компонент

Метод главных компонент (МГК) был предложен Пирсоном в 1901 году и затем вновь открыт и детально разработан Хоттелингом /1933/. Ему посвящено большое количество исследований, и он широко представлен в литературных источниках, обратившись к которым можно получить сведения о методе главных компонент с различной степенью детализации и математической строгости (например, Айвазян С. А. и др., 1974, 1983, 1989). В данном разделе не ставится цель добиться подробного изложения всех особенностей МГК. Сконцентрируем свое внимание на основных феноменах метода главных компонент.

Метод главных компонент осуществляет переход к новой системе координат y1,...,ур в исходном пространстве признаков x1,...,xp которая является системой ортнормированных линейных комбинаций

где mi — математическое ожидание признака xi. Линейные комбинации выбираются таким образом, что среди всех возможных линейных нормированных комбинаций исходных признаков первая главная компонента у1(х) обладает наибольшей дисперсией. Геометрически это выглядит как ориентация новой координатной оси у1 вдоль направления наибольшей вытянутости эллипсоида рассеивания объектов исследуемой выборки в пространстве признаков x1,...,xp. Вторая главная компонента имеет наибольшую дисперсию среди всех оставшихся линейных преобразований, некоррелированных с первой главной компонентой. Она интерпретируется как направление наибольшей вытянутости эллипсоида рассеивания, перпендикулярное первой главной компоненте. Следующие главные компоненты определяются по аналогичной схеме.

Вычисление коэффициентов главных компонент wij основано на том факте, что векторы wi= (w11,...,wpl)', ... , wp = (w1p, ... ,wpp)' являются собственными (характеристическими) векторами корреляционной матрицы S. В свою очередь, соответствующие собственные числа этой матрицы равны дисперсиям проекций множества объектов на оси главных компонент.

Алгоритмы, обеспечивающие выполнение метода главных компонент, входят практически во все пакеты статистических программ.

Факторный анализ

В описанном выше методе главных компонент под критерием автоинформативности пространства признаков подразумевается, что ценную для диагностики информацию можно отразить в линейной модели, которая соответствует новой координатной оси в данном пространстве с максимальной дисперсией распределения проекций исследуемых объектов. Такой подход является продуктивным, когда явное большинство заданий «чернового» варианта теста согласованно «работает» на проявление тестируемого свойства и подавляет влияние иррелевантных факторов на распределение объектов. Также положительный результат будет получен при сравнительно небольшом объеме группы связанных информативных признаков, но при несогласованном взаимодействии посторонних факторов, под влиянием которых не нарушается однородность эллипсоида рассеивания, а лишь уменьшается вытянутость распределения объектов вдоль направления диагностируемой тенденции. В отличие от метода главных компонент факторный анализ основан не на дисперсионном критерии автоинформативности системы признаков, а ориентирован на объяснение имеющихся между признаками корреляций. Поэтому факторный анализ применяется в более сложных случаях совместного проявления на структуре экспериментальных данных тестируемого и иррелевантного свойств объектов, сопоставимых по степени внутренней согласованности, а также для выделения группы диагностических показателей из общего исходного множества признаков.

Основная модель факторного анализа записывается следующей системой равенств /Налимов В. В., 1971/

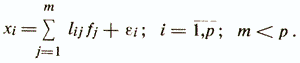
То есть полагается, что значения каждого признака xi могут быть выражены взвешенной суммой латентных переменных (простых факторов) fi, количество которых меньше числа исходных признаков, и остаточным членомεi с дисперсией σ2(εi), действующей только на xi, который называют специфическим фактором. Коэффициенты lijназываются нагрузкой i-й переменной на j-й фактор или нагрузкой j-го фактора на i-ю переменную. В самой простой модели факторного анализа считается, что факторы fj взаимно независимы и их дисперсии равны единице, а случайные величины εi тоже независимы друг от друга и от какого-либо фактора fj. Максимально возможное количество факторов m при заданном числе признаков р определяется неравенством

(р+m)<(р—m)2,

которое должно выполняться, чтобы задача не вырождалась в тривиальную. Данное неравенство получается на основании подсчета степеней свободы, имеющихся в задаче /Лоули Д. и др., 1967/. Сумму квадратов нагрузок в формуле основной модели факторного анализа называют общностью соответствующего признака xi и чем больше это значение, тем лучше описывается признак xi выделенными факторами fj. Общность есть часть дисперсии признака, которую объясняют факторы. В свою очередь, ε2i показывает, какая часть дисперсии исходного признака остается необъясненной при используемом наборе факторов и данную величину называют специфичностью признака. Таким образом,

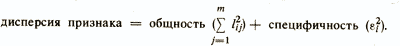
Основное соотношение факторного анализа показывает, что коэффициент корреляции любых двух признаков xi и хj можно выразить суммой произведения нагрузок некоррелированных факторов

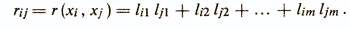
Задачу факторного анализа нельзя решить однозначно. Равенства основной модели факторного анализа не поддаются непосредственной проверке, так как р исходных признаков задается через (р+m) других переменных — простых и специфических факторов. Поэтому представление корреляционной матрицы факторами, как говорят, ее факторизацию, можно произвести бесконечно большим числом способов. Об этом говорит сайт https://intellect.icu . Если удалось произвести факторизацию корреляционной матрицы с помощью некоторой матрицы факторных нагрузок F, то любое линейное ортогональное преобразование F (ортогональное вращение) приведет к такой же факторизации /Налимов В. В., 1971/.

Существующие программы вычисления нагрузок начинают работать с m =1 (однофакторная модель) /Александров В. В. и др., 1990/. Затем проверяется, насколько корреляционная матрица, восстановленная по однофакторной модели в соответствии с основным соотношением факторного анализа, отличается от корреляционной матрицы исходных данных. Если однофакторная модель признается неудовлетворительной, то испытывается модель с m=2 и т. д. до тех пор, пока при некотором m не будет достигнута адекватность или число факторов в модели не превысит максимально допустимое. В последнем случае говорят, что адекватной модели факторного анализа не существует. Если факторная модель существует, то производится вращение полученной системы общих факторов, так как значения факторных нагрузок и нагрузок на факторы есть лишь одно из возможных решений основной модели. Вращение факторов может производиться разными способами. Наиболее часто это вращение осуществляется таким образом, чтобы как можно большее число факторных нагрузок стало нулями и каждый фактор по возможности описывал группу сильно коррелированных признаков. Также можно вращать факторы до тех пор, пока не получатся результаты, поддающиеся содержательной интерпретации. Можно, например, потребовать, чтобы один фактор был нагружен преимущественно признаками одного типа, а другой — признаками другого типа. Или, скажем, можно потребовать, чтобы исчезли какие-то трудно интерпретируемые нагрузки с отрицательными знаками. Нередко исследователи идут дальше и рассматривают прямоугольную систему факторов как частный случай косоугольной, то есть ради содержания жертвуют условием некоррелированности факторов.

В завершение всей процедуры факторного анализа с помощью математических преобразований выражают факторы fj через исходные признаки, то есть получают в явном виде параметры линейной диагностической модели.

Известно большое количество методов факторного анализа (ротаций, максимального правдоподобия и др.). Нередко в одном и том же пакете программ анализа данных реализовано сразу несколько версий таких методов и у исследователей возникает правомерный вопрос о том, какой из них лучше. В этом вопросе наше мнение совпадает с /Александров В. В. и др., 1990/, где утверждается, что практически все методы дают весьма близкие результаты. Там же приводятся слова одного из основоположников современного факторного анализа Г. Хармана: «Ни в одной из работ не было показано, что какой-либо один метод приближается к "истинным" значениям общностей лучше, чем другие методы... Выбор среди группы методов "наилучшего" производится в основном с точки зрения вычислительных удобств, а также склонностей и привязанностей исследователя, которому тот или иной метод казался более адекватным его представлениям об общности» /Харман Г., 1972, с. 97/.

У факторного анализа есть много сторонников и много оппонентов. Но, как справедливо заметил В. В. Налимов: «...У психологов и социологов не оставалось других путей, и они изучили эти два приема (факторный анализ и метод главных компонент, — В. Д.) со всей обстоятельностью» /Налимов В. В., 1971, с. 100/. Для более подробного ознакомления с факторным анализом и его методами может быть рекомендована литература /Лоули Д., и др., 1967; Харман Г., 1972; Айвазян С. А. и др., 1974; Иберла К., 1980/.

Метод контрастных групп

Исходной информацией при использовании метода контрастных групп, помимо таблицы экспериментальных данных с результатами обследования испытуемых «черновым» вариантом психодиагностического теста, является также «черновая» версия линейного правила вычисления тестируемого показателя. Эта «черновая» версия может быть составлена экспериментатором, исходя из его теоретических представлений о том, какие признаки и с какими весами должны быть включены в линейную диагностическую модель. Кроме того, «черновая» версия может быть почерпнута из литературных источников, когда у экспериментатора возникает потребность адаптировать опубликованный психодиагностический тест к новым условиям. Метод контрастных групп применяется также в составе процедуры повышения внутренней согласованности заданий ранее отработанного теста.

В основе метода контрастных групп лежит гипотеза о том, что значительная часть «черновой» версии диагностической модели подобрана или угадана правильно. То есть в правую часть уравнения уч = уч(х) вошло достаточно много признаков, согласованно отражающих тестируемое свойство. В то же время в «черновой» версии уч(х) определенная доля признаков приходится на ненужный или даже вредный балласт, от которого нужно избавиться. Как и во всех других методах, опирающихся на категорию внутренней согласованности, это означает, что в пространстве признаков, включенных в исходную диагностическую модель, распределение объектов вписывается в эллипсоид рассеивания, вытянутый вдоль направления диагностируемой тенденции. В свою очередь, влияние информационного балласта выражается в уменьшении такой вытянутости эллипсоида рассеивания, так как «шумящие» признаки увеличивают разброс исследуемых объектов по всем другим направлениям. При этом «зашумление» основной тенденции будет тем сильнее, чем ближе к центру распределения располагаются диагностируемые объекты, и тем слабее, чем ближе к полюсам главной оси эллипсоида рассеивания находятся рассматриваемые объекты. Это связано с тем, что попадание объектов в крайние области объясняется, главным образом, кумулятивным эффектом согласованного взаимодействия информативных признаков. Описанные представления о структуре экспериментальных данных лежат в основе следующей процедуры, которая будет рассмотрена на примере анализа пунктов при конструировании тест-опросников /Шмелев А. Г., Похилько В. И., 1985/.

Сначала назначаются исходные шкальные ключи (веса) w˚j для пунктов теста (дихотомических признаков) хj. Для каждого i-го испытуемого подсчитывается суммарный тестовый балл

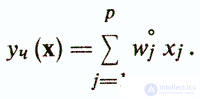
Обычно абсолютные значения весов wj определяют приблизительно и часто берут равными единице. Поэтому направление

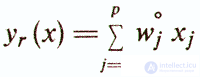
будет несколько отличаться от направления главной диагонали эллипсоида рассеивания у(х) (рис. 3).

Рис. 3. Иллюстрация метода контрастных групп

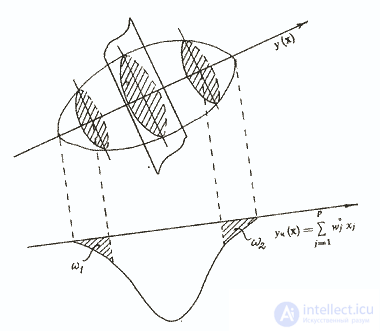
Но если ориентировочно уч(х) правильно отражает диагностируемое свойство, то на краях распределения суммарного балла, построенного по всем объектам исследуемой выборки, можно выделить контрастные группы ω1 и ω2, в которые войдут объекты с минимальными погрешностями, вносимыми «шумящими» признаками. Эти группы не должны быть слишком малы. Для нормального распределения, как правило, берут контрастные группы объемом 27% от общего объема выборки, для более плоского — 33%. В принципе считается приемлемой любая цифра от 25 до 33% /Анастази А., 1982/. Следующий шаг заключается в определении степени связи каждого пункта с дихотомической переменной — номером контрастной группы. Мерой этой связи может служить так называемый коэффициент различения, представляющий собой разницу процентов того или иного ответа на анализируемый пункт в полярных группах испытуемых. Наиболее часто используется коэффициент связи Пирсона φ, который затем сравнивается с граничным значением

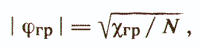
где χ2гр — стандартный квантиль распределения χ2 с одной степенью свободы. Обычно ориентируются на 5% и 1% уровни \ значимости, для которых значение χ2 равно 3,84 и 6,63 соответственно. Если для і-гo пункта |φі|<|φгр|, то весовому коэффициенту wi присваивается значение нуля, то есть признак хi исключается из линейной диагностической модели уч(х). Таким образом проверяются все пункты «чернового» варианта теста. Затем для оставшихся пунктов вся процедура снова полностью повторяется и т. д.

На практике не встречается случая, когда окончательно отобранные с помощью приведенной процедуры информативные признаки абсолютно бы совпали с первоначально заданными. Сходимость этой процедуры зависит от исходного соотношения «хороших» и «плохих» заданий теста. По-видимому, для диагностических моделей, основанных на принципе внутренней согласованности используемых признаков, в каждой конкретной задаче существует определенный порог соотношения информативных и «шумящих» признаков, начиная с которого возможно возникновение эффекта самоорганизации или самосовершенствования диагностической модели посредством описанного выше алгоритма.

3. Методы, использующие внешний критерий

Выделяют три основные группы внешних критериев: экспертные, экспериментальные и «жизненные».

К числу экспертных критериев относятся оценки, суждения, заключения об испытуемых, вынесенные экспертом или группой экспертов, в качестве которых выступают специалисты, педагоги, руководители, психологи, врачи и т. п. Объективизация внешнего критерия достигается увеличением числа экспертов. При этом применяется четыре возможных метода определения экспертного критерия: коллективная оценка, средневзвешенная оценка, ранжирование, парное сравнение.

При коллективной оценке эксперты совместно оценивают испытуемого по диагностируемому качеству с помощью предложенной разработчиком теста балльной шкалы. Условием коллективной оценки является выработка общего компромиссного мнения. Достижение консенсуса при коллективной оценке зависит от личностных особенностей и характера группового взаимодействия экспертов. Также немаловажным фактором является разрешающая способность заданной оценочной шкалы. Чем меньше баллов в этой шкале, тем легче достигается соглашение между экспертами, но тем грубее выставляемые ими оценки. В то же время излишняя детализация шкалы не только не приводит к повышению точности оценки, а нередко вызывает ненужные и длительные разногласия экспертов. Поэтому обычно применяются оцененные шкалы, содержащие до 10 баллов.

При средневзвешенном оценивании эксперты независимо друг от друга определяют значения критериального показателя, которые затем усредняются. Здесь следует обратить внимание на то, что перед усреднением оценок из них должны быть исключены явно отклоняющиеся, аномальные оценки. Метод ранжирования в отличие от средневзвешенной оценки связан не с проецированием того или иного качества испытуемого на числовую оценочную шкалу, а с определением рангов выраженности исследуемого качества в группе испытуемых. Полученные ранговые места при независимом оценивании также могут усредняться, но корректнее в данном случае пользоваться медианными оценками: каждому испытуемому приписывается ранг, равный медиане ряда рангов, присвоенных ему всеми экспертами..

При использовании слабо дифференцированных оценочных показателей или при низкой квалификации экспертов применяется метод парного сравнения. Задача экспертов состоит в попарной расстановке испытуемых по позициям альтернативных признаков («общительный-замкнутый», «завистливый-бескорыстный» и т. п.). Показателем места, занимаемого в ряду других, наиболее часто служит общее число предпочтений данного испытуемого. Этот показатель обычно нормируется по отношению к числу экспертов и общему количеству сравниваемых испы­туемых и выражается в процентах.

Более сложные варианты приведения результатов ранжирования и парного сравнения испытуемых к одномерному критериальному показателю связаны с применением компьютерных алгоритмов многомерного шкалирования. Метрические и неметрические методы многомерного шкалирования в достаточно полном объеме представлены в /Айвазян С. А. и др., 1989/. Там же приведены ссылки на литературу для более подробного ознакомления с этими методами.

На практике значительно большее распространение получили экспериментальные критерии внешней информативности. Это обусловлено в основном трудностью организации экспертиз и использования обычных количественных методов измерения требуемого качества. Экспериментальными критериями служат результаты одновременного и независимого обследования испытуемых другим тестом, который считается апробированным и предположительно измеряющим то же свойство, что и конструируемый тест. Естественно, что просто конструирование теста-дубликата имеет смысл в случае необходимости создания параллельной формы. Наиболее целесообразен такой подход, когда ставится задача улучшить собственно диагностические и эксплуатационные характеристики известного психодиагностического инструментария.

В качестве жизненных критериев используют объективные социально-демографические и биографические данные (стаж, образование, профессия, прием или увольнение с работы), показатели успеваемости, производственные показатели эффективности выполнения отдельных видов профессиональной деятельности (рисование, моделирование, музыка, составление рассказа и т. д.). Эти критерии наиболее часто применяются для конструирования тестов способностей к обучению, дости­жений в отдельных

продолжение следует...

Продолжение:

Часть 1 Конструирование психодиагностических тестов: традиционные математические модели и алгоритмы
Часть 2 2. Методы, основанные на критерии автоинформативности системы признаков - Конструирование
Часть 3 Дискриминантный анализ - Конструирование психодиагностических тестов: традиционные математические модели и
Часть 4 Типологический подход - Конструирование психодиагностических тестов: традиционные математические модели и
Часть 5 - Конструирование психодиагностических тестов: традиционные математические модели и алгоритмы
Часть 6 - Конструирование психодиагностических тестов: традиционные математические модели и алгоритмы

Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.