Лекция
Это продолжение увлекательной статьи про имитация психологической интуиции с помощью искусственных нейронных сетей.
...
>.
Как видно, в каждом из этих определений 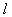 играет роль характеристики «запаса устойчивости» точки минимума.
играет роль характеристики «запаса устойчивости» точки минимума.
Кроме 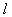 в качестве характеристики устойчивости точки минимума используют «нормированный» показатель
в качестве характеристики устойчивости точки минимума используют «нормированный» показатель 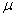 , называемый обусловленностью точки минимума
, называемый обусловленностью точки минимума 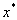 .
.

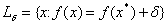
Можно сказать, что 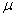 характеризует степень вытянутости линий уровня
характеризует степень вытянутости линий уровня 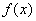 в окрестности
в окрестности 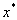 — «овражность» функции (чем больше
— «овражность» функции (чем больше 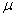 , тем более «овражный» характер функции).
, тем более «овражный» характер функции).
Наиболее важны в идейном отношении следующие методы безусловной оптимизации: градиентный и Ньютона.
Идея градиентного метода заключается в том, чтобы достигнуть экстремума путем итерационного повторения процедуры последовательных приближений начиная с начального приближения 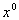 в соответствии с формулой
в соответствии с формулой 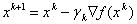 , где
, где 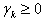 — длина шага.
— длина шага.
Сходимость данного метода подтверждается в доказательстве следующей теоремы:
Пусть функция 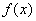 дифференцируема на
дифференцируема на 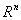 , градиент
, градиент 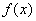 удовлетворяет условию Липшица:
удовлетворяет условию Липшица:
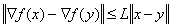 ,
,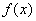 ограничена снизу:
ограничена снизу: 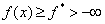
и 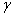 удовлетворяет условию
удовлетворяет условию 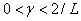
Тогда в градиентном методе с постоянным шагом 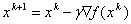 градиент стремится к 0:
градиент стремится к 0: 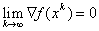 , а функция
, а функция 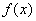 монотонно убывает:
монотонно убывает: 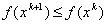
Для сильно выпуклых функций доказываются более сильные утверждения о сходимости градиентного метода.
При решении задачи оптимизации методом Ньютона используется подход, заключающийся в итерационном процессе вида
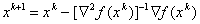
и в нахождении точки экстремума как решения системы из n уравнений с n неизвестными
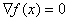 .
.В методе Ньютона производится линеаризация уравнений в точке 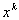 и решение линеаризованной системы вида
и решение линеаризованной системы вида
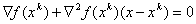
Анализ достоинств и недостатков итерационных методов оптимизации можно свести в таблицу (см. табл. 3).
Таблица 3. Достоинства и недостатки итерационных методов оптимизации
| Метод | Достоинства | Недостатки |
| Градиентный | Глобальная сходимость, слабые требования к 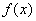 , простота вычислений , простота вычислений |
Медленная сходимость, необходимость выбора 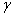 . . |
| Ньютона | Быстрая сходимость | Локальная сходимость, жесткие требования к 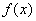 , большой объем вычислений. , большой объем вычислений. |
Видно, что достоинства и недостатки этих методов взаимно дополнительны, что делает привлекательной идею создания модификаций этих методов, объединяющих достоинства методов и свободных от их недостатков.
Модификацией градиентного метода является метод наискорейшего спуска:
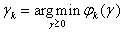 ,
, 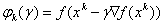
Модификация метода Ньютона с целью придания ему свойства глобальной сходимости возможна, например, способом регулировки длины шага:
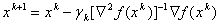
Такой метод называют демпфированным методом Ньютона. Возможные подходы к способу выбора шага 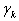 :
:
— Вычисление по формуле
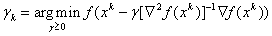 ;
;— Итерационный алгоритм, заключающийся в последовательном дроблении шага 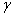 на константу
на константу 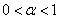 начиная со значения
начиная со значения 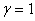 до выполнения условия
до выполнения условия
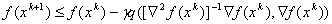 ,
, 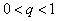
или условия 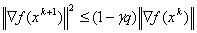 ,
, 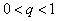
Демпфированный метод Ньютона глобально сходится для гладких сильно выпуклых функций.
Помимо одношаговых методов, к которым относятся градиентный метод и метод Ньютона, существует целый класс многошаговых методов, использующих для оптимизации информацию, полученную с предыдущих шагов. К ним относятся:
— 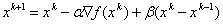 , где
, где 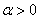 ,
, 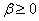 — некоторые параметры. Введение инерции движения (член
— некоторые параметры. Введение инерции движения (член 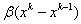 ) в некоторых случаях приводит к ускорению сходимости за счет выравнивания движения по «овражистому» рельефу функции;
) в некоторых случаях приводит к ускорению сходимости за счет выравнивания движения по «овражистому» рельефу функции;
— Метод сопряженных градиентов. Здесь параметры оптимизации находятся из решения двумерной задачи оптимизации:
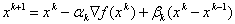 ,
,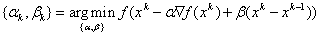
Кроме всех вышеперечисленных методов оптимизации существует еще класс методов, основанных на идее восстановления квадратичной аппроксимации функции по значениям ее градиентов в ряде точек. К ним относятся:
— 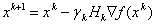 , где матрица
, где матрица 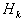 пересчитывается рекуррентно на основе информации, полученной на k-йитерации, так что
пересчитывается рекуррентно на основе информации, полученной на k-йитерации, так что 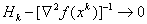 . К числу таких методов относятся ДФП (метод Давидона-Флетчера-Пауэлла) и BFGS или БФГШ (метод Бройдена-Флетчера-Гольдфарба-Шанно) [46].
. К числу таких методов относятся ДФП (метод Давидона-Флетчера-Пауэлла) и BFGS или БФГШ (метод Бройдена-Флетчера-Гольдфарба-Шанно) [46].
— 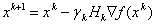 ,
, 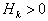 , может рассматриваться как градиентный в метрике
, может рассматриваться как градиентный в метрике 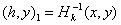 , а оптимальным выбором метрики является
, а оптимальным выбором метрики является 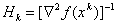 .
.
В данной работе задачи распознавания образов и восстановления зависимостей будут решаться в основном с применением нейронных сетей. Обзор данной темы основан на - , -[15], [22],[23], [32]-[34], [36]-[41], [59], [64], [67]-[70], [83]-[88].
Нейронная сеть представляет собой структуру взаимосвязанных клеточных автоматов, состоящую из следующих основных элементов:
Нейрон — элемент, преобразующий входной сигнал по функции:
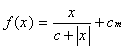
где x — входной сигнал, c — параметр, определяющий крутизну графика пороговой функции, а cm — параметр спонтанной активности нейрона.
Сумматор — элемент, осуществляющий суммирование сигналов поступающих на его вход:
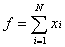
Синапс — элемент, осуществляющий линейную передачу сигнала:
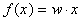
где w — «вес» соответствующего синапса.
Сеть состоит из нейронов, соединенных синапсами через сумматоры по следующей схеме:
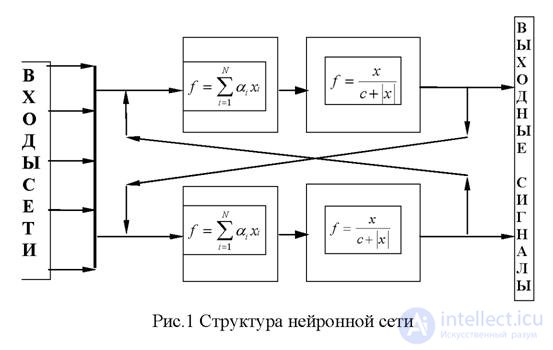
Сеть функционирует дискретно по времени (тактами). Тогда синапсы можно разделить на «синапсы связи», которые передают сигналы в данном такте, и на «синапсы памяти», которые передают сигнал с выхода нейрона на его вход на следующем такте функционирования. Сигналы, возникающие в процессе работы сети разделяются на прямые (используемые при выдаче результата сетью) и двойственные (использующиеся при обучении) и могут быть заданы следующими формулами:
Для i-го нейрона на такте времени T:

где mi0 — параметр инциации сети, xi1 — входные сигналы сети, поступающие на данный нейрон, fiT — выходной сигнал нейрона на такте времени T, Ai1 — входной параметр i-го нейрона на первом такте функционирования сети, AiT — входной сигнал i-го нейрона на такте времени T, aji — вес синапса от j-го нейрона к i-му, aMi — вес синапся памяти i-го нейрона, ai1 — параметр нейрона и ai2 — параметр спонтанной активности нейрона, AiT-1 — входной сигнал i-го нейрона на такте T-1, fjT-1 — выходной сигнал j-го нейрона на такте T-1 и fiT,A — производная i-го нейрона по его входному сигналу.
Для синапса связи от i-го нейрона к j-му:

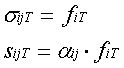
где sjT — входной сигнал синапса от i-го нейрона к j-му, fiT — выходной сигнал i-го нейрона, aij — вес данного синапса, sijT — выходной сигнал синапса на такте времени T.
Для синапса памяти i-го нейрона: 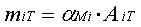
В данной задаче обучение будет происходить по «коннекционистской» модели, то есть за счет подстройки весов синапсов.
Суть обучения состоит в минимизации функции ошибки 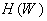 , где W— карта весов синапсов. Для решения задачи минимизации необходимо вычисление градиента функции по подстраиваемым параметрам:
, где W— карта весов синапсов. Для решения задачи минимизации необходимо вычисление градиента функции по подстраиваемым параметрам:
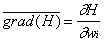
Расчет градиента ведется при обратном отсчете тактов времени 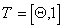 по следующим формулам:
по следующим формулам:
Для синапса связи:
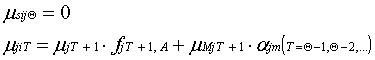
Для синапса памяти:
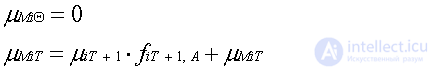
Окончательно после прохождения q тактов времени частные производные по весам синапсов будут иметь вид для синапсов памяти и для синапсов связи соответственно:

1. Применяемый в психодиагностике математический аппарат недостаточно удовлетворяет современным требованиям.
2. Насущной является потребность во внедрении в психодиагностические методики математического аппарата, связанного с распознаванием образов и восстановлением зависимостей.
3. Существующие математические методы и алгоритмы слишком сложны и трудоемки для применения их специалистами — предметниками, в том числе и психодиагностами и не позволяют компьютерным методикам непосредственно по прецедентам перенимать опыт человека-специалиста.
4. Использование математического аппарата нейронных сетей при создании нейросетевых экспертных психологических систем позволяет свести к минимуму требования к математической подготовке их создателей.
Специфические особенности математического аппарата нейронных сетей, детально описанные в [36], [41] и опыт их применения в различных областях знания (см. например , , [10], [13], [84], [86]) подсказали возможность решения при их помощи и психологических задач.
Предполагалось проверить несколько возможностей использования нейронных сетей, а именно:
— Во первых — ожидалось решение серьезной проблемы, возникающей у разработчиков и пользователей компьютерных психологических тестов, а именно адаптивности методик. Математическое построение современных объективных диагностических тестов основано на сравнении, сопоставлении выявленного состояния с нормой, эталоном [21], [71]. Однако понятно, что нормы выработанные для одной социокультурной группы вовсе не обязательно являются таковыми же для другой (в качестве примера можно привести сложности, которые приходится преодолевать при адаптации зарубежных методик). Нейросетевые же имитаторы обладают полезной в данном случае особенностью дообучаться по тому материалу, который предоставит конкретный исследователь.
— Во вторых — предполагалось использование нейросетевого имитатора как рабочего средства исследователя.
— В третьих — оценка возможности создания при помощи нейронных сетей новых, нестандартных тестовых методик. Предполагалось проверить возможность выдачи непосредственных рекомендаций по преобразованию реального состояния объекта, минуя стадию выставления диагноза (построения «измеренной индивидуальности» [26]).
Исследование было выполнено с применением нейросетевых программных имитаторов объединения «НейроКомп» [36], [41], [70], [85], [87] на психологическом материале, собранном в Красноярском гарнизонном военном госпитале.
В первую очередь предстояло выяснить, доступен ли нейросетям тот уровень диагностики, который уже достигнут при помощи стандартных психологических тестов. Для получения результатов максимальной достоверности была выбрана достаточно проверенная клинической практикой психологическая методика ЛОБИ [57] (Личностный Опросник Бехтеревского института). Кроме того, немаловажным фактором в выборе именно этого теста было и то, что методика четко алгоритмизована и имеет реализацию в виде компьютерного теста.
Итак задачей эксперимента было определить, насколько адекватно нейросетевой имитатор может воспроизвести результаты типовой психологической методики в постановке диагноза пациенту.
Рассмотрев данную задачу, а также имеющиеся в наличии нейросетевые программы было решено воспользоваться нейросетевым имитатором MultiNeuron (описание пакета см. в [85], [87]).
Пакет программ MultiNeuron представляет собой программный имитатор нейрокомпьютера, реализованный на IBM PC/AT, и, в числе прочих функций, предназначен для решения задач n-арной классификации. Данный пакет программ позволяет создавать и обучать нейросеть для того, чтобы по набору входных сигналов (например, по ответам на заданные вопросы) определить принадлежность объекта к одному из n (n<9) классов, которые далее будем нумеровать целыми числами от 1 до n. Необходимая для обучения выборка была составлена из результатов обследования по методике ЛОБИ 203 призывников и военнослужащих проходящих лечение в Красноярском гарнизонном военном госпитале и его сотрудников. При этом было получено 12 файлов задачника для MultiNeuron (по гармоническому типу выборка содержала недостаточно данных — 1 пример с наличием данного типа).
Задачники были сформированы из строк ответов, представляющих собой цепочку из 162 сигналов, каждый из которых отвечал за 1 из вопросов опросника ЛОБИ по следующему принципу: -1 — выбран негативный ответ на данный вопрос, 1 — выбран позитивный ответ, 0 — вопрос не выбран. Данная система обозначений была выбрана, исходя из желательности нормировки входных сигналов, подаваемых на вход нейронов на интервале [-1,1]. Ответ задавался классами, 1 класс — тип отсутствует, 2 класс — тип диагностируется. При этом для чистоты эксперимента по собственно типам реакции на стресс было принято решение отказаться от диагностики негативного отношения к исследованию и исключить из обучающей выборки такие примеры.
В общих чертах суть экспериментов сводилась к следующему: часть примеров исходной выборки случайным образом исключалась из процесса обучения. После этого нейронная сеть обучалась на оставшихся, а отобранные примеры составляли тестовую выборку, на которой проверялось, насколько вычисленные ответы нейронной сети соответствуют истинным.
В процессе обучения нейронных сетей с различными характеристиками автор пришел к выводу, что для данной задачи можно ограничиться числом нейронов равным 2 (то есть по 1 нейрону на каждый из классов). Наилучшие результаты при тестировании на проверочной выборке показали сети с характеристическим числом нейронов c=0.4.
Для подробной обработки была взята выборка, отвечающая за эргопатический тип ЛОБИ. Серия экспериментов по обучению сети показала, что полносвязная сеть, обучаемая на выборке из 152 примеров, не показывает результат лучше, чем 90% правильных ответов (в среднем же — около 75%). Тот же результат подтвердился при проведении сквозного тестирования, когда обучение производилось на 202 примерах, а тестировался 1. После обучения 203 сетей по такой методике был получен сходный результат — уверенно правильно было опознано 176 примера (86.7%), неуверенно правильно — 4 (1.97%), неверно — 28 (13.79%), то есть общий процент правильных ответов составил 88.67. Следует, однако, отметить, что рост числа примеров обучающей выборки до 200 позволили улучшить число правильных ответов до гарантированной величины 88.67% (см. выше). Следует предположить, что дальнейшее увеличение обучающей выборки позволит и еще улучшить данный результат. Кроме того, причина ошибок в определении эргопатического типа по ЛОБИ может скрываться в недостаточном числе примеров с наличием данного типа (отношение примеров с наличием и отсутствием типа составляет 29:174). Это подтверждается также и тем, что среди примеров с наличием типа процент неверных ответов ( 12 из 29 или 41.38%) несопоставимо выше чем в выборке в целом. Можно, таким образом, сделать вывод, что нейронные сети при использовании определенных методов улучшения результатов (см. ниже) позволяют создавать компьютерные психологические тесты, не уступающие ныне применяющимся методикам, но обладающие новым и очень важным на практике свойством — адаптивностью.
Представляет также интерес результат, полученный при оценке значимости входных сигналов (соответственно — вопросов ЛОБИ).
Пусть некоторый функциональный элемент нейронной сети преобразует поступающий на него вектор сигналов A по какому-либо закону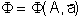 , где
, где 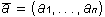 — вектор адаптивных параметров. Пусть H — функция оценки, явно зависящая от выходных сигналов нейросети и неявно от входных сигналов и параметров нейросети. При двойственном функционировании будут вычислены частные производные
— вектор адаптивных параметров. Пусть H — функция оценки, явно зависящая от выходных сигналов нейросети и неявно от входных сигналов и параметров нейросети. При двойственном функционировании будут вычислены частные производные 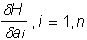 для элемента v. Эти производные показывают чувствительность оценки к изменению параметра
для элемента v. Эти производные показывают чувствительность оценки к изменению параметра , чем больше
, чем больше 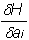 , тем сильнее изменится H при изменении этого параметра для данного примера. Может также оказаться, что производная по какому-либо параметру очень мала по сравнению с другими, это означает, что параметр практически не меняется при обучении. Таким образом, можно выделить группу параметров, к изменениям которых нейросеть наименее чувствительна, и в процессе обучения их вовсе не изменять. Разумеется, что для определения группы наименьшей или наибольшей чувствительности необходимо использовать частные производные функции оценки по параметрам в нескольких циклах обучения и для всех примеров задачника. Во время обучения нейросети динамика снижения функции оценки меняется на разных этапах обучения. Бывает важным определить, какие входные сигналы на данном этапе обучения существенны для нейросети, а какие нет. Такая информация полезна в тех случаях, когда размерность вектора входных сигналов велика и время обучения также оставляет желать лучшего, поскольку позволяет уменьшить размерность вектора входных сигналов без ухудшения обучаемости нейросети.
, тем сильнее изменится H при изменении этого параметра для данного примера. Может также оказаться, что производная по какому-либо параметру очень мала по сравнению с другими, это означает, что параметр практически не меняется при обучении. Таким образом, можно выделить группу параметров, к изменениям которых нейросеть наименее чувствительна, и в процессе обучения их вовсе не изменять. Разумеется, что для определения группы наименьшей или наибольшей чувствительности необходимо использовать частные производные функции оценки по параметрам в нескольких циклах обучения и для всех примеров задачника. Во время обучения нейросети динамика снижения функции оценки меняется на разных этапах обучения. Бывает важным определить, какие входные сигналы на данном этапе обучения существенны для нейросети, а какие нет. Такая информация полезна в тех случаях, когда размерность вектора входных сигналов велика и время обучения также оставляет желать лучшего, поскольку позволяет уменьшить размерность вектора входных сигналов без ухудшения обучаемости нейросети.
Предлагается следующий алгоритм решения такой задачи: через несколько циклов после начала обучения нейронной сети включаем процедуру вычисления показателей значимости. Момент начала запуска данной процедуры желательно подбирать индивидуально в каждом конкретном случае, поскольку в первые несколько циклов обучения нейросеть как-бы «рыскает» в поисках нужного направления и показатели значимости могут меняться на диаметрально противоположные. Далее происходит несколько циклов обучения, в ходе которых накапливаются показатели чувствительности в какой-либо норме.
1) 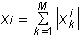

2) 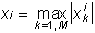
где 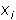 — норма для i-го сигнала,
— норма для i-го сигнала, 
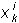
 — оценка значимости i-го сигнала в k-м примере, M — число циклов подсчета значимости. После того, как показатели
— оценка значимости i-го сигнала в k-м примере, M — число циклов подсчета значимости. После того, как показатели 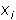 подсчитаны, можно произвести уменьшение числа входных сигналов. Уменьшение следует производить исходя из того, что чем меньше значение
подсчитаны, можно произвести уменьшение числа входных сигналов. Уменьшение следует производить исходя из того, что чем меньше значение 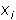
продолжение следует...
Часть 1 Имитация психологической интуиции с помощью искусственных нейронных сетей
Часть 2 1.4. Перспективные алгоритмы построения психодиагностических методик - Имитация психологической интуиции
Часть 3 1.7 Нейронные сети - Имитация психологической интуиции с помощью искусственных
Часть 4 Глава 3. Интуитивное предсказание нейросетями взаимоотношений - Имитация психологической интуиции
Часть 5 Приложение. Психологический опросник А.Г. Копытова - Имитация психологической интуиции с
Ответы на вопросы для самопроверки пишите в комментариях, мы проверим, или же задавайте свой вопрос по данной теме.
Комментарии
Оставить комментарий
Математические методы в психологии
Термины: Математические методы в психологии