1.4. Перспективные алгоритмы построения психодиагностических методик - Имитация психологической интуиции

Это продолжение увлекательной статьи про имитация психологической интуиции с помощью искусственных нейронных сетей.

...

style="text-align:justify">Для стратегий, основанных на автоинформативности экспериментальных данных, важной категорией является согласованность заданий теста.

Согласованность измеряемых реакций испытуемых на тестовые стимулы означает, что они должны иметь статистическую направленность на выражение общей, главной тенденции теста.

На стратегии, основанной на автоинформативности экспериментальных данных, строятся конструирование диагностического алгоритма при помощи метода главных компонент [17], [18], [19], факторного анализа [66] и метода контрастных групп [97].

2. Стратегия, основанная на критериях внешней информативности. Внешняя информация может быть представлена в виде привязки к объектам значений «зависимой» переменной, измеренной в количественной шкале, в виде номера однородного по тестируемому свойству класса, в виде порядкового номера (ранга) объекта в ряду всех объектов, упорядоченных по степени проявления диагностируемого свойства или в виде совокупности значений набора внешних (не включенных в таблицу экспериментальных данных) признаков, характеризующих тестируемый психологический феномен.

Методы, основанные на внешней информативности признаков, принято подразделять на экспертные, экспериментальные и жизненные.

К числу экспертных критериев относят оценки, суждения, заключения об испытуемых, вынесенные одним экспертом или их группой.

Экспериментальными критериями служат результаты одновременного и независимого исследования испытуемого другим тестом, который считается апробированным и измеряющим то же свойство, что и конструируемый тест.

В качестве жизненных критериев используются объективные социально — демографические и биографические данные.

На стратегии, основанной на внешней информативности экспериментальных данных, строятся конструирование диагностического алгоритма при помощи регрессионного анализа, дискриминантного анализа [49] и типологического подхода [60], [99].

Наиболее широко в настоящее время употребляются линейные диагностические модели. Однако в условиях неоднородности обучающей выборки они обладают практической успешностью не выше 70-80% [60].

Построенная диагностическая модель может считаться психодиагностическим тестом только после прохождения ею испытаний на предмет проверки психометрических свойств — надежности и валидности [20],[27].

Надежность теста — характеристика методики, отражающая точность психодиагностических измерений, а также устойчивость результатов теста к воздействию посторонних случайных факторов [27].

Валидность — мера соответствия тестовых оценок представлениям о сущности свойств или их роли в той или иной деятельности [60].

1.4. Перспективные алгоритмы построения психодиагностических методик

Перспективным направлением в построении психодиагностических методик в настоящее время считается использование аппарата теории распознавания образов , [13], [47].

Классификация методов распознавания образов многообразна. Выделяются параметрические, непараметрические и эвристические методы, существуют классификации основанные на терминологии сложившихся научных школ. В [52] методы распознавания образов классифицируются следующим образом:

— методы, основанные на принципе разделения;

— статистические методы;

— методы типа «потенциальных функций»;

— методы вычисления оценок (голосования);

— методы, основанные на аппарате исчисления высказываний.

Кроме того существенным для метода, основанного на теории распознавания образов, может быть способ представления знаний. В настоящее время выделяют два основных способа [78]:

1. Интенсиональные представления — схемы связей между атрибутами (признаками)

2. Экстенсиональные представления — конкретные факты (объекты, примеры).

Группа интенсиональных методов распознавания образов включает в себя следующие подклассы:

1) Методы, основанные на оценках плотностей распределения значений признаков (методы непараметрической статистики) [18].

2) Методы, основанные на предположениях о классе решающих функций (методы, использующие в качестве решающего алгоритма минимизацию функционала риска или ошибки) , [15],[36], [41], [94].

3) Логические методы, базирующиеся на аппарате алгебры логики и позволяющие оперировать информацией, заключенной не только в отдельных признаках, но и в сочетании их значений [49].

4) Лингвистические (структурные) методы, основанные на использовании специальных грамматик, порождающих языки, с помощью которых может описываться совокупность свойств распознаваемых объектов [93].

Группа экстенсиональных методов включает в себя:

1) Метод сравнения с прототипом, применяющийся когда распознаваемые классы отображаются в пространстве признаков компактными геометрическими группировками.

2) Метод k-ближайших соседей, в котором решение об отнесении объекта к какому-либо классу принимается на основе информации о принадлежности k его ближайших соседей.

3) Алгоритм вычисления оценок (голосования), состоящий в вычислении приоритетов (оценок сходства), характеризующего «близость» распознаваемого и эталонных объектов по системе ансамблей признаков, представляющей собой систему подмножеств заданного множества признаков [51],[52],[53].

При сравнении экстенсиональных и интенсиональных методов распознавания образов в [47] употребляется следующая аналогия: интенсиональные методы соответствуют левополушарному способу мышления, основанному на знаниях о статических и динамических закономерностях структуры воспринимаемой информации; экстенсиональные же методы соответствуют правополушарному способу мышления, основанному на целостном отображении объектов мира.

1.5. Методы восстановления зависимостей

Наиболее широко в данной работе будут рассмотрены методы построения психодиагностических методик на базе интенсиональных методов, основанных на предположениях о классе решающих функций. Поэтому рассмотрим их более подробно.

Основным достоинством методов, основанных на предположении о классе решающих функций является ясность математической постановки задачи распознавания как поиска экстремума. Многообразие методов этой группы объясняется широким спектром используемых функционалов качества решающего правила и алгоритмов поиска экстремума. Обобщением данного класса алгоритмов является метод стохастической аппроксимации [94].

В данном классе алгоритмов распознавания образов содержательная формулировка задачи согласно [29] ставится следующим образом:

Имеется некоторое множество наблюдений, которые относятся к p различных классов. Требуется, используя информацию об этих наблюдениях и их классификациях, найти такое правило, с помощью которого можно было бы с минимальным количеством ошибок классифицировать вновь появляющиеся наблюдения.

Наблюдение задается вектором x, а его классификация — числом ().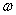

Таким образом, требуется, имея последовательность из l наблюдений и классификаций 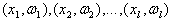построить такое решающее правило , которое с возможно меньшим числом ошибок классифицировало бы новые наблюдения.

Для формализации термина «ошибка» принимается предположение о том, что существует некоторое правило 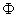, определяющее для каждого вектора x классификацию 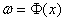, которая называется «истинной». Ошибкой классификации вектора x с помощью правила 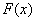называется такая классификация, при которо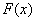й и 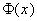не совпадают.

Далее предполагается, что в пространстве векторов x существует неизвестная нам вероятностная мера (обозначаемая плотность 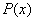). В соответствии с 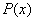случайно и независимо появляются ситуации x, которые классифицируются с помощью правила 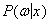. Таким образом определяется обучающая последовательность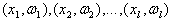

Качество решающего правила 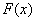записывается в ви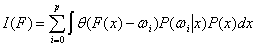де , где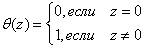

Проблема следовательно заключается в построении решающего правила 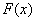таким образом, чтобы минимизировать функционал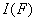

Сходной с задачей распознавания образов является задача восстановления регрессии, предпосылки к которой формулируются следующим образом:

Два множества элементов связаны функциональной зависимостью, если каждому элементу x может быть поставлен в соответствие элемент y. Эта зависимость называется функцией, если множество x — векторы, а множество y — скаляры. Однако существуют и такие зависимости, где каждому вектору x ставится в зависимость число y, полученное с помощью случайного испытания, согласно условной плотности 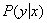. Иначе говоря, каждому x ставится в соответствие закон 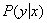, согласно которому в случайном испытании реализуется выбор y.

Существование таких связей отражает наличие стохастических зависимостей между вектором x и скаляром и скаляром y. Полное знание стохастической зависимости требует восстановления условной плотности 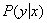, однако, данная задача весьма трудна и на практике (например, в задачах обработки результатов измерения) может быть сужена до задачи определения функции условного математического ожидания. Эта суженная задача формулируется следующим образом: определить функцию условного математического ожидания, то есть функцию, которая каждому x ставит в соответствие число y(x), равное математическому ожиданию скаляра y: 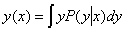. Функция y(x) называется функцией регрессии, а задача восстановления функции условного математического ожидания — задачей восстановления регрессии.

Строгая постановка задачи такова:

В некоторой среде, характеризующейся плотностью распределения вероятности P(x), случайно и независимо появляются ситуации x. В этой среде функционирует преобразователь, который каждому вектору x ставит в соответствие число y, полученное в результате реализации случайного испытания, согласно закону 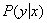. Свойства среды P(x) и закон 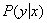неизвестны, однако известно, что существует регрессия 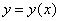. Требуется по случайной независимой выборке пар 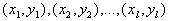восстановить регрессию, то есть в классе функций 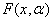отыскать функцию 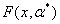, наиболее близкую к регрессии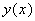

Задача восстановления регрессии является одной из основных задач прикладной статистики. К ней приводится проблема интерпретации прямых экспериментов.

Задача решается в следующих предположениях:

—

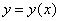
— Целью исследования является определение зависимости 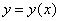в ситуации, когда в любой точке x может быть проведен прямой эксперимент по определению этой зависимости, то есть проведены прямые измерения величины 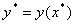. Однако вследствие несовершенства эксперимента результат измерения определит истинную величину с некоторой случайной ошибкой, то есть в каждой точке x удается определить не величину 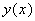, а величину 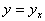, где 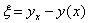— ошибка эксперимента,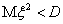

— Ни в одной точке x условия эксперимента не допускают систематической ошибки, то есть математическое ожидание измерения функции в каждой фиксированной точке равно значению функции 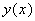в этой точке: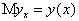

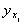— Случайные величины и независимы.

В этих условиях необходимо по конечному числу прямых экспериментов восстановить функцию 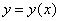. Об этом говорит сайт https://intellect.icu . Требуемая зависимость есть регрессия, а суть проблемы состоит в отыскании регрессии по последовательности пар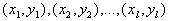

Задача восстановления регрессии принято сводить к проблеме минимизации функционала 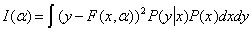на множестве 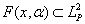(интегрируемых с квадратом по мере 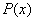функций) в ситуации, когда плотность неизвестна, но зато задана случайная и независимая выборка пар .

1.6. Алгоритмы и методы безусловной оптимизации

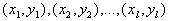Как было показано в предыдущем параграфе данной главы, решение основных задач восстановления зависимостей достигается при помощи процедуры оптимизации функционала качества.

Ее решение будет рассмотрено в подходах задачи безусловной минимизации гладкой функции 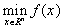[77].

Данная задача непосредственно связана с условиями существования экстремума в точке:

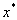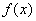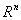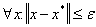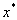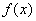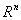— Необходимое условие первого порядка. Точка называется локальным минимумом на , если найдется для . Согласно теореме Ферма если — точка минимума на и 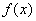дифференцируема в 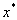, то

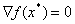
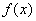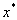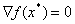— Достаточное условие первого порядка. Если — выпуклая функция, дифференцируемая в точке и , то 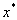— точка глобального минимум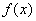а на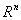

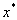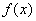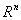— Необходимое условие второго порядка. Если — точка минимума на и 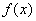дважды дифференцируема в ней, то

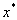
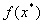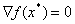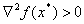— Достаточное условие второго порядка. Если в точке дважды дифференцируема, выполнено необходимое условие первого порядка () и , то 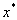— точка локального минимума.

Условия экстремума являются основой, на которой строятся методы решения оптимизационных задач. В ряде случаев условия экстремума хотя и не дают возможности явного нахождения решения, но сообщают много информации об его свойствах.

Кроме того, доказательство условий экстремума или вид этих условий часто указывают путь построения методов оптимизации.

При обосновании методов приходится делать ряд предположений. Обычно при этом требуется, чтобы в точке 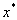выполнялось достаточное условие экстремума. Таким образом, условия экстремума фигурируют в теоремах о сходимости методов.

И, наконец, сами доказательства сходимости обычно строятся на том, что показывается, как «невязка» в условии экстремума стремится к нулю.

При решении оптимизационных задач существенны требования существования, единственности и устойчивости решения.

Существование точки минимума проверяется при помощи теоремы Вейерштрасса:

Пусть 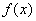непрерывна на 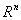и множество 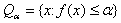для некоторого 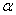непусто и ограничено. Тогда существует точка глобального минимум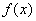а на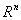

При анализе единственности точки экстремума применяются следующие рассуждения:

Точка минимума называется локально единственной, если в некоторой ее окрестности нет других локальных минимумов. Считается, что 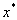— невырожденная точка минимума, если в ней выполнено достаточное условие экстремума второго порядка (,).

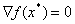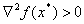Доказано, что точка минимума (строго) выпуклой функции (глобально) единственна.

Проблема устойчивости решения возникает в связи со следующим кругом вопросов:

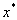—–локального минимума 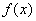называется локально устойчивой, если к ней сходится любая локальная минимизирующая последовательность, то есть если найдется такое, что из следует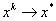

При обсуждении проблемы устойчивости решения задачи оптимизации можно выделить следующие важные теоремы.

— Точка локального минимума непрерывной функции 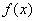локально устойчива тогда и только тогда, когда она локально единственна.

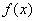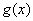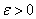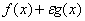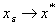— Пусть — локально устойчивая точка минимума непрерывной функции , а — непрерывная функция. Тогда для достаточно малых функция имеет локально единственную точку минимума в окрестности и при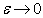

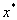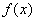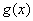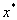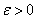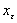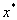— Пусть — невырожденная точка минимума , а функция непрерывно дифференцируема в окрестности точки . Тогда для достаточно малых существует — локальная точка минимума функции в окрестности , причем

Помимо качественной характеристики точки минимума (устойчива она или нет) существенным является вопрос количественной оценки устойчивости. Такие оценки, позволяющие судить о близости точки 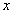к решению 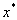, если 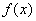близко к 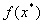записываются следующим образом:

Для сильно выпуклых функций:

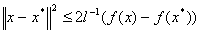
где 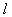— константа сильной выпуклости.

Для невырожденной точки минимума:

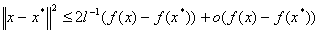
где 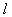— наименьшее собственное значение матрицы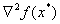

продолжение следует...

Продолжение:

Часть 1 Имитация психологической интуиции с помощью искусственных нейронных сетей
Часть 2 1.4. Перспективные алгоритмы построения психодиагностических методик - Имитация психологической интуиции
Часть 3 1.7 Нейронные сети - Имитация психологической интуиции с помощью искусственных
Часть 4 Глава 3. Интуитивное предсказание нейросетями взаимоотношений - Имитация психологической интуиции
Часть 5 Приложение. Психологический опросник А.Г. Копытова - Имитация психологической интуиции с