1. Нареч. Формой напоминая треугольник (1*); в виде треугольника.

 ... 2 понятий совсем просто формулируются некоторые теоремы . геометрии Например , в любом треугольнике (в остро , прямо , и в тупоугольном .) 3 произведения пред - и поствысоты совпадают Для остро-и ... ... равенства в параллелограмме суммы квадратов сторон и суммы квадратов . диагоналей ): где - медианы к сторонам треугольника соответственно В частности , сумма квадратов медиан произвольного треугольника составляет 3 /4 ... (Планометрия)
... 2 понятий совсем просто формулируются некоторые теоремы . геометрии Например , в любом треугольнике (в остро , прямо , и в тупоугольном .) 3 произведения пред - и поствысоты совпадают Для остро-и ... ... равенства в параллелограмме суммы квадратов сторон и суммы квадратов . диагоналей ): где - медианы к сторонам треугольника соответственно В частности , сумма квадратов медиан произвольного треугольника составляет 3 /4 ... (Планометрия)
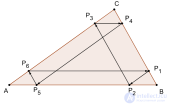 ... окружности Таких прямых может существовать три , две или одна Замечание об изо-прямых треугольника В английской литературе вводится понятие бисекции (Bisection ), как разделение чего-либо . на две равные ... ... через эту точку провести 3 прямые , параллельные сторонам треугольника ., то они отсекут на сторонах треугольника 3 равных внутренних (серединных ).отрезка Другая формулировка последнего утверждения : Отрезки ... (Планометрия)
... окружности Таких прямых может существовать три , две или одна Замечание об изо-прямых треугольника В английской литературе вводится понятие бисекции (Bisection ), как разделение чего-либо . на две равные ... ... через эту точку провести 3 прямые , параллельные сторонам треугольника ., то они отсекут на сторонах треугольника 3 равных внутренних (серединных ).отрезка Другая формулировка последнего утверждения : Отрезки ... (Планометрия)
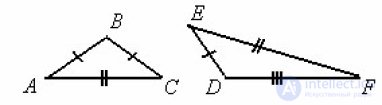 ... равны Эти стороны называются боковыми , третья сторона называется основанием В равнобедренном треугольнике углы при основании равны Равносторонним или правильным называется треугольник , у которого все три ... ... Равносторонним или правильным называется треугольник , у которого все три стороны . равны В равностороннем треугольнике все углы равны 60 °, а центры вписанной . и описанной окружностей совпадают Равносторонний ... (Планометрия)
... равны Эти стороны называются боковыми , третья сторона называется основанием В равнобедренном треугольнике углы при основании равны Равносторонним или правильным называется треугольник , у которого все три ... ... Равносторонним или правильным называется треугольник , у которого все три стороны . равны В равностороннем треугольнике все углы равны 60 °, а центры вписанной . и описанной окружностей совпадают Равносторонний ... (Планометрия)
 ... состоит в замене звена замкнутой ломаной АВ на. два звена АС и ВС при условии, что треугольник ABC не . пересекает других звеньев замкнутой ломаной данного узла , а также ... ... изотопии [АВ ] -> []U.[C B] Без Ьграничения общности будем считать , что на каждом шаге для. соответствующего треугольника ABC звенья [DA ] и [BE ], выходящие из концов отрезка [АВ ], не пересекают ... (Теории узлов, зацеплений, кос и их инвариантов)
... состоит в замене звена замкнутой ломаной АВ на. два звена АС и ВС при условии, что треугольник ABC не . пересекает других звеньев замкнутой ломаной данного узла , а также ... ... изотопии [АВ ] -> []U.[C B] Без Ьграничения общности будем считать , что на каждом шаге для. соответствующего треугольника ABC звенья [DA ] и [BE ], выходящие из концов отрезка [АВ ], не пересекают ... (Теории узлов, зацеплений, кос и их инвариантов)
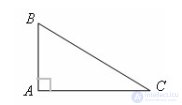 ... Треугольник называется прямоугольным , если у него есть прямой угол Сторона прямоугольного треугольника , противолежащая прямому ... ... и AB – катеты , BC – гипотенуза Теорема Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе . и катету другого прямоугольного треугольника , то такие треугольники равны Доказательство ... (Планометрия)
... Треугольник называется прямоугольным , если у него есть прямой угол Сторона прямоугольного треугольника , противолежащая прямому ... ... и AB – катеты , BC – гипотенуза Теорема Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе . и катету другого прямоугольного треугольника , то такие треугольники равны Доказательство ... (Планометрия)
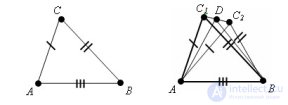 ... Если три стороны одного треугольника равны соответственно трем сторонам . другого треугольника , то такие треугольники равны Доказательство Пусть треугольники ABC и такие, что AB =, AC .=, BC = Требуется ... ... равны Доказательство Пусть треугольники ABC и такие, что AB =, AC .=, BC = Требуется доказать , что треугольники равны Допустим , что треугольники не равны Тогда ∠ A ≠ ∠ , ∠ B ≠ ∠ , ∠ C ≠ ∠ одновременно Иначе треугольники были ... (Планометрия)
... Если три стороны одного треугольника равны соответственно трем сторонам . другого треугольника , то такие треугольники равны Доказательство Пусть треугольники ABC и такие, что AB =, AC .=, BC = Требуется ... ... равны Доказательство Пусть треугольники ABC и такие, что AB =, AC .=, BC = Требуется доказать , что треугольники равны Допустим , что треугольники не равны Тогда ∠ A ≠ ∠ , ∠ B ≠ ∠ , ∠ C ≠ ∠ одновременно Иначе треугольники были ... (Планометрия)
Комментарии
Оставить комментарий