1 Движения Рейдемейстера. Арифметика узлов § 1. Полигональные узлы и движения Рейдемейстера кратко

Привет, Вы узнаете о том , что такое 1 Движения Рейдемейстера. Арифметика узлов § 1. Полигональные узлы и движения Рейдемейстера, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое 1 Движения Рейдемейстера. Арифметика узлов § 1. Полигональные узлы и движения Рейдемейстера , настоятельно рекомендую прочитать все из категории Теории узлов, зацеплений, кос и их инвариантов.

В данной лекции речь пойдет об узлах, их плоских
диаграммах и движениях Рейдемейстера, а также о полугрупповой
структуре на множестве узлов, которая изоморфна полугрупповой структуре
на полугруппе натуральных чисел по умножению. Такое сходство
структур на множестве узлов и множестве натуральных чисел дает основания
говорить об арифметике узлов. Будет также дано много примеров.
Хотя сопутствующий материал по геометрии и топологии будет
рассказан и в рамках настоящего спецкурса, слушателям предлагается
ознакомиться с основными определениями, например, в [126]. С
некоторыми наглядными топологическими конструкциями читатель может
ознакомиться в [122].

§ 1. Полигональные узлы и движения Рейдемейстера

Так как узел представляет собой гладкое вложение окружности
в R3, его можно как угодно близко аппроксимировать (приблизить)
вложением замкнутой ломаной в R3, не выходя из его изотопического
класса.
Определение 1.1. Вложение замкнутой ломаной в R3 называется
полигональным (многоугольным) узлом.
Определение 1.2. Узел (зацепление) называется ручным, если он
изотопен полигональному узлу (зацеплению); в противном случае
узел (зацепление) называется диким.
Замечание 1.1. Различие между ручными и дикими узлами имеет
первостепенную важность. Почти все утверждения настоящей книги применимы
только к ручным узлам. Все С1 -гладкие узлы являются ручными,
доказательство см. в [104]. В дальнейшем мы будем предполагать все узлы гладкими и,
следовательно, ручными, если не оговорено противное.
Упражнение 1.1. Определите аккуратно полигональное зацепление.
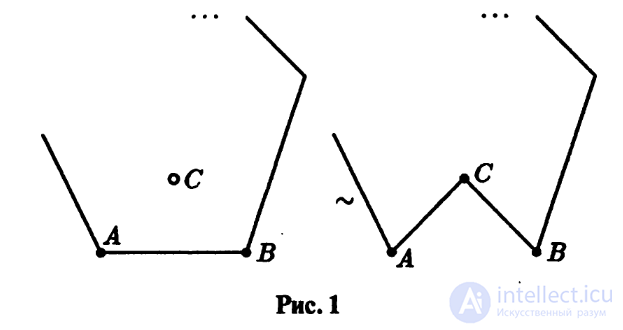
Определение 1.3. Скажем, что два полигональных узла
(зацепления) изотопны, если одно из них может быть переведено в другое

многократной композицией так называемой элементарной
изотопии, которая состоит в замене звена замкнутой ломаной АВ на два
звена АС и ВС при условии, что треугольник ABC не пересекает
других звеньев замкнутой ломаной данного узла, а также обратного
к элементарной изотопии преобразования, см. рис. 1.

Для полигональных узлов, как и для гладких, можно
рассматривать плоские диаграммы с проходами и переходами, при этом по графу
с проходами и переходами можно восстановить полигональный узел
с точностью до изотопии; в частности, при достаточно хорошей
аппроксимации гладкого узла полигональным плоская диаграмма будет
иметь такую же комбинаторную структуру.
Упражнение 1.2. Об этом говорит сайт https://intellect.icu . Покажите, что все полигональные узлы с числом
звеньев, меньшим шести, тривиальны.
Упражнение 1.3. Приведите пример полигонального трилистника с
шестью звеньями.
Определение 1.4. Назовем плоской изотопией плоской
диаграммы гладкого узла (зацепления) гомеоморфизм плоскости на себя,
не меняющий комбинаторной структуры 2-комплекса,
получаемого делением плоскости графом проекции узла на клетки и
сохраняющий структуру проходов и переходов в вершинах проекции.
Замечание 1.2. Аналогично определяемая плоская изотопия полигонального
узла не должна быть чувствительна к двухвалентным вершинам; так, разбивая
ребро на два дополнительной вершиной, мы получаем диаграмму, являющуюся
плоско-изотопной исходной.
Замечание 1.3. Плоская изотопия не меняет изотопического класса узла
в пространстве R3.
Теорема 1.1 (Рейдемейстер, [79]). Две плоские диаграммы D1 и D2
гладких узлов (зацеплении) порождают изотопные узлы (зацепления)
тогда и только тогда, когда D1 переводится в D2 с помощью
последовательного применения плоской изотопии и трех движений
Рейдемейстера 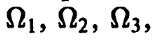см.рис.2.

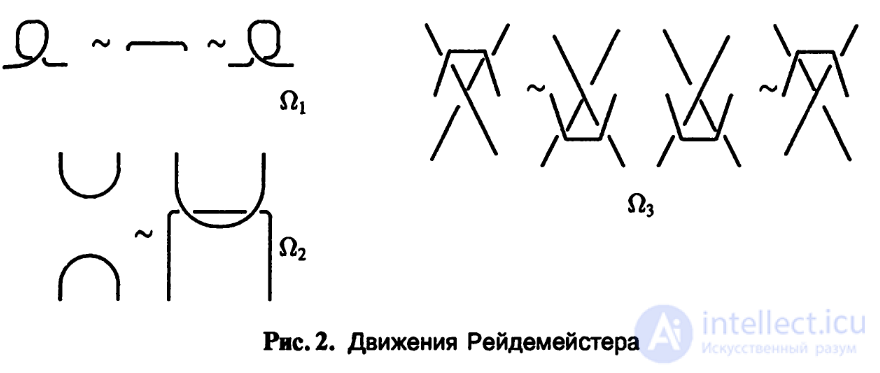
Одно из доказательств этой теоремы основано на понятии
коразмерности; здесь мы приведем другое доказательство, основанное
на применении полигональных узлов (зацеплений).
Доказательство. В одну сторону доказательство очевидно. Для этого
достаточно лишь проверить, что все движения Пх,£12,&з не меняют
изотопического класса узла.
Докажем утверждение теоремы в обратную сторону. Итак, пусть
два изотопных узла К\ и Кг заданы своими плоскими
диаграммами D\ и 2>2 с проходами и переходами. Тогда существует непрерывная
изотопия узла К\ в узел Ki в пространстве R3. Аппроксимируем эти
узлы полигональными узлами К[ и К'2 и рассмотрим изотопию от К[
к К'2, состоящую из элементарных изотопии [АВ] —> [j4C]U[C.B].
Без Ьграничения общности будем считать, что на каждом шаге для
соответствующего треугольника ABC звенья [DA] и [BE], выходящие
из концов отрезка [АВ], не пересекают внутренности
треугольника ABC. В противном случае этого легко можно добиться с помощью
движения £1\.
Легко видеть, что компоненты пересечения проекции треугольника
ABC с Lq, где Хо — проекция данного зацепления на плоскость ABC,
бывают верхние и нижние, т. е. соответствующие им ветви зацепления L
лежат под (или над) плоскостью ABC.
Разобьем треугольник ABC на мелкие треугольники четырех
типов, стороны которых не содержат вершин проекции Lo (см. рис. 3).
Треугольник первого типа содержит ровно один перекресток Lo, при
этом ветви Lo пересекают ровно две стороны этого треугольника.
Треугольник второго типа содержит ровно одну вершину L0 и части
выходящих из нее звеньев. Треугольник третьего типа содержит часть
ровно одного звена Lo и не содержит вершин. Наконец, треугольник

четвертого типа не содержит ни вершин, ни ребер (на рис. 3 он не
изображен).

Такую триангуляцию треугольника ABC можно построить
следующим образом. Сначала для каждого перекрестка и каждой вершины
строим треугольники первого и второго типов, а затем разрезаем
оставшуюся часть треугольника ABC на треугольники третьего и четвертого
типов.
Теперь вместо исходного элементарного преобразования
треугольника ABC будем совершать элементарные преобразования четырех
типов для маленьких треугольников. На рис. 3 видно, что движение для
треугольника первого типа соответствует комбинации третьего и вторых
движений Рейдемейстера Пз> ДОЯ треугольников второго или
третьего типа — 1^2 или плоской изотопии. Движение для треугольника
четвертого типа представляет собой плоскую изотопию.
Тем самым теорема доказана. ■
Упражнение 1.4. Покажите, что два варианта третьего движения
Рейдемейстера, показанные на рис.2, зависимы, т.е. любое из них выводится
из другого, а также второго движения Рейдемейстера.
При этом все три движения Рейдемейстера fii,ft2>^3 являются
независимыми друг от друга. Их независимость будет показана в
приложении 1.

Определение 1.5. Узел называется обратимым, если он изотопен
узлу, получаемому из него заменой ориентации.
Замечание 1.4. Не нужно путать обратимость узла с наличием у него
обратного (в смысле композиции, см. опр. 1.6).
Упражнение 1.5. С помощью движений Рейдемейстера покажите, что
правый и левый трилистники являются обратимыми узлами.
Существование необратимых узлов долгое время было проблемой.
Она была решена лишь в 1964 году, см. [82].
Пример необратимого узла показан на рис. 4.

Исследование, описанное в статье про 1 Движения Рейдемейстера. Арифметика узлов § 1. Полигональные узлы и движения Рейдемейстера, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое 1 Движения Рейдемейстера. Арифметика узлов § 1. Полигональные узлы и движения Рейдемейстера и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теории узлов, зацеплений, кос и их инвариантов