Введение. Основные определения Теории узлов

Привет, Вы узнаете о том , что такое теория узлов, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое теория узлов, теория кос , настоятельно рекомендую прочитать все из категории Теории узлов, зацеплений, кос и их инвариантов.

теория узлов , которой посвящен настоящий спецкурс, возникла
как математическая теория в конце 18 - начале 19 века; Hai
протяжении более сотни лет ей занимались такие выдающиеся математики,
как А. Т. Вандермонд, К.-Ф. Гаусс (нашедший замечательную
электромагнитную формулу для вычисления коэффициента зацепления [37]),
Ф. Клейн, а позже — М. Ден [28]. Ее систематическое изложение
началось с восьмидесятых годов 19 века, когда математики и физики начали
составлять таблицы узлов под влиянием идей физика У. Томпсона
(впоследствии известного как лорд Кельвин), полагавшего, что
узлы должны соответствовать химическим элементам. Однако настоящие
прорывы в теории узлов начались во второй половине 20 века и связаны
в первую очередь с именами Дж. X. Конвея, В. Джонса и В. А. Васильева,
а позднее — М, Л. Концевича, В. Г. Тураева, М. Н. Гусарова.
Теория узлов происходит из красивой и на первый взгляд очень
простой топологической задачи, для решения которой, как оказалось,
требуется весьма сложный и глубокий математический аппарат,
связанный с топологией, теорией дискриминантов, теорией групп и алгебр
Ли, теорией мультипликативного интеграла, тензорной алгеброй, и др.
При этом узловая тематика является бурно развивающейся; за
последние годы важные работы в теории узлов (Джонс, Уиттен, Дринфельд
в 1990, Концевич в 1998) были оценены Филдсовскими медалями.
Кроме того, теория узлов служит для построения других теорий,
ярким примером которых является исчисление Кирби — теория
кодирования трехмерных многообразий.
Итак, начнем с определения узла. Под узлом будем понимать
непрерывное вложение окружности S1 в пространство R3 (или в
сферу 53). Наглядно узел можно представить в виде веревки с сомкнутыми

концами. Мы можем деформировать пространство R
(соответственно 53), при этом узел будет двигаться и растягиваться (но не рваться!)
и оставаться несамопересекающимся. Более строго, два узла называются
изотопными, если один из них можно перевести в другой гладким
гомеоморфизмом объемлющего пространства R3 или 53 на себя, гомотопным
тождественному отображению в классе гладких гомеоморфизмов. При
этом хотелось бы знать, какие узлы изотопны, а какие не изотопны.
Такая задача называется задачей распознавания узлов. Можно говорить
об изотопических классах узлов. Можно также говорить об инвариантах
узлов, т. е. функциях на изотопических классах узлов, или функциях
на узлах, не меняющихся при изотопиях узлов.
Частным случаем задачи распознавания узлов является задача
распознавания тривиального узла, являющегося самым простым узлом
(узлом, представляющим границу диска, вложенного в трехмерное
пространство).
Оба эти вопроса, на первый взгляд очень простые, являются очень
трудными. На самом деле к данному моменту эти задачи уже решены,
но их решение составляет огромную книгу [41], является
алгоритмически сложным и очень трудно читается. С основными этапами решения
этой проблемы можно познакомиться в статье [116].
В данном курсе мы постараемся частично ответить на вопрос
об изотопности и неизотопности узлов. Как правило, чтобы
установить изотопность узлов, нужно перевести один узел в другой с
помощью некоторых преобразований (например, движений Рейдемейстера,
о которых будет сказано позже), а для установления неизотопности
достаточно найти инвариант, различающий эти узлы.
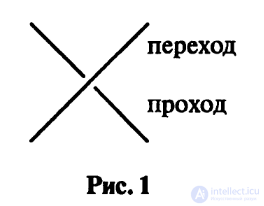
Обычно узлы изображаются следующим образом. Пусть дан узел,
т. е. задано отображение / : S1 —► R3. Рассмотрим некоторую плоскость
h Е R3 и проекцию узла (строго говоря, проекцию образа функции /)
на Данную плоскость. В случае плоскости общего положения, т. е. «почти
всегда», эта проекция будет представлять собой вложенный в плоскость
граф с вершинами кратности четыре. При этом в каждой вершине
графа (которую также можно назвать перекрестком) пересекаются образы
проекций разных дуг («кусочков») узла, и, если мы зададим
направление х, перпендикулярное h, то для каждой такой вершины можно будет
сказать, какая дуга проходит выше, а какая — ниже (чья координата х
больше, а чья — меньше). Отметим это на плоскости так, как показано
на рис. 1.
Такие типы символического изображения дуг узлов
называются соответственно переходами и проходами, а такой граф с
проходами и переходами называется плоской диаграммой узла. Соответственно

четырехвалентный граф без указания проходов и переходов называется
тенью узла.

Минимальное количество перекрестков плоской диаграммы для
данного изотопического класса узла называется сложностью узла.
Итак, каждый узел допускает некоторую плоскую диаграмму с
проходами и переходами. При этом возникает естественный вопрос:
а не потеряли ли мы какую-нибудь информацию об узле, кодируя
его таким образом.
Легко можно проделать следующее
Упражнение 0.1. Узлы, имеющие в качестве плоских диаграмм
изоморфные графы с одинаковым образом расставленными проходами и переходами,
изотопны.
Приведем несколько примеров.
Пример 0.1.

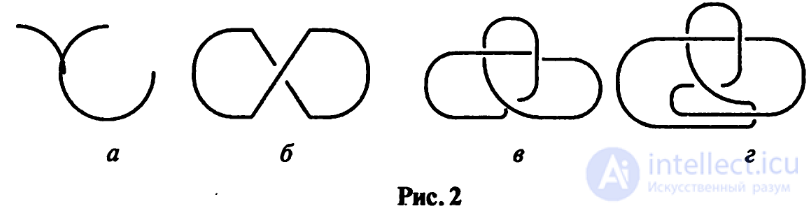
Узел, изотопный узлу, имеющему диаграмму без пересечений (рис. 2 л),
называется тривиальным узлом. На рис. 2 б изображена другая плоская
диаграмма тривиального узла. Узел на рис. 2 в называется трилистником, а узел
на рис. 2 г называется восьмеркой. Оба эти узла — нетривиальные, при этом они
не изотопны друг другу.
Для каждого узла можно построить его зеркальное отражение —
узел, получаемый отражением данного относительно какой-либо
плоскости. Диаграммы зеркального отражения узла получаются заменой
на диаграммах исходного всех типов перекрестков (проходов на
Переходы и наоборот). Узел называется зеркальным, если он изотопен своему
зеркальному отражению.
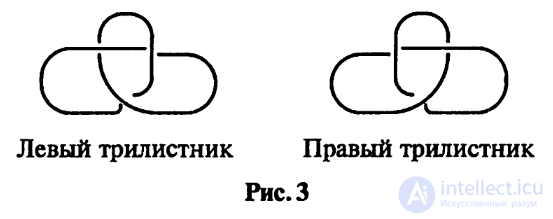
Пример 0.2. Трилистник не является зеркальным узлом (доказательство
будет приведено позже).

Таким образом, можно говорить о двух трилистниках — правом
и левом.

Упражнение 0.2. Показать, что восьмерка является зеркальным узлом.
Во многих задачах теории узлов рассматривают ориентированные
узлы — углы, на которых задано направление обхода, или же
отображения ориентированной окружности в R3. Об этом говорит сайт https://intellect.icu . При этом при изотопии узлов
требуется условие сохранения ориентации.
Параллельно с теорией узлов развивалась также и теория
зацеплений, имеющая много общего в подходах с теорией узлов. Под
зацеплением будем понимать достаточно гладкое вложение нескольких
окружностей в R3, при этом требуя, чтобы образы разных точек как
одной, так и разных окружностей не совпадали. Каждый узел,
представляющий собой отображение в R3 одной из окружностей, называется
компонентой зацепления. Естественным образом определяется изотопия
зацеплений (с помощью гладкого гомеоморфизма объемлющего
пространства), плоские диаграммы зацеплений и инварианты зацеплений. При
этом для задания ориентированного зацепления нужно ориентировать все
его компоненты. Есть и другой подход к изотопии зацеплений, в
котором в процессе «изотопии» каждой компоненте зацепления
позволяется самопересекаться, но различным компонентам пересекаться нельзя.
Об этом можно прочесть в замечательной статье [68] Джона Милнора,
который ввел так называемые ^-инварианты для классификации
зацеплений с точностью до такой «изотопии». Тривиальным зацеплением из п
компонент называется зацепление, изотопное зацеплению, диаграмма
которого представляет собой п окружностей (без перекрестков).
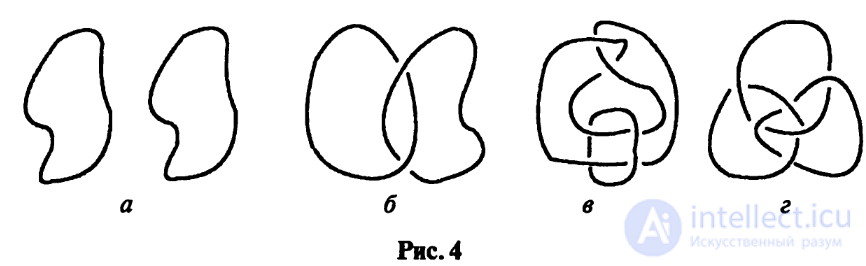
Пример 0.3.
На рис. 4 а изображено тривиальное зацепление из двух компонент.
На рис. 46, в, г изображены зацепления, называемые зацеплением Хопфа,
зацеплением Уайтхеда и кольцами Борромео соответственно. Первые два зацепления
названы так в честь топологов X. Хопфа и Дж. Уайтхеда, а третье — в честь
итальянского рода Борромео, на гербе которого оно было изображено. Все
они — нетривиальные (это будет показано ниже, когда мы научимся считать
значения инвариантов, различающих узлы или зацепления), при этом нетрудно
заметить, что каждые две окружности из трех между собой «незацеплены».

Поговорим немного об инвариантах. Самым первым и самым
простым инвариантом узлов и зацеплений являлась фундаментальная
группа дополнения к узлу (зацеплению), которой будет посвящена
отдельная лекция. Этот инвариант является чисто топологическим, при этом
он очень сильный, т. е. хорошо различает узлы (в частности,
тривиальный узел и тривиальное зацепление из любого числа компонент),
но не различает некоторые неизотопные зацепления. При этом такое
«решение» проблемы распознавания узлов не является полным, так как
оно сводится к, вообще говоря, нерешаемой проблеме распознавания
групп, заданных с помощью образующих и соотношений.
В 1923 году американский математик Александер в своих работах
[2,3] ввел полиномиальный инвариант узлов и зацеплений, основанный
на фундаментальной группе дополнения к узлу.
Затем в 1932 году вышла в свет книга немецкого тополога
Рейдемейстера «Knotentheorie», в которой описывался инвариант
Александера, был приведен список движений Рейдемейстера и доказана
теорема о том, что любые две плоские диаграммы дают изотопные
узлы только в случае существования цепочки движений от одной
диаграммы к другой, а также приведена таблица изотопических классов
узлов сложности до семи включительно. Существует также английский
перевод этой книги [79]. Для доказательства инвариантности той или
иной функции на узлах, как правило, проверяют ее инвариантность
относительно движений Рейдемейстера.
Из книг, содержащих сведения об узлах «тех времен», отмечу
книги Кроуэлла и Фокса (на русском языке) [104], а также Бурде
и Цишанга [19].
Обзоры по маломерной топологии и теории узлов можно найти
в [130, 129].
Следующим этапом в теории узлов и зацеплений было
открытие полинома Конвея, см. [25], основанное на так называемых skein
relations, или соотношениях типа Конвея, при этом являющееся
комбинаторным, основанным на понятии плоской диаграммы узла. Полином
Александера мог быть также интерпретирован в соотношениях типа
Конвея, мало того, Александер (см. [2]) знал о соотношениях «типа

Конвея», но лишь Конвей обнаружил, что skein-relations могут быть
использованы в качестве аксиоматического подхода.
Основным прорывом было изобретение полинома Джонса,
основанного на соотношениях типа Конвея. С помощью полинома Джонса
были решены некоторые важные проблемы в теории узлов, например
проблема Тейта, см. [80].
Позже появлялись другие полиномы, основанные на соотношениях
типа Конвея: Кауфмана, HOMFLYh др. При этом HOMFLY — не есть
фамилия одного автора, это — аббревиатура от первых букв фамилий
авторов Hoste, Ocneanu, Millett, Freyd, Lickorish и Yetter, см. [42].
Самым сильным из этих полиномов является полином Джонса
от двух переменных, так как каждый из оставшихся получается из него
некоторой заменой переменных, при этом полином Джонса различает
любые два узла, различаемые каким-либо из вышеперечисленных
полиномов. Существует также и полином Джонса от одной переменной,
см. [44, 45].
Задание узлов с помощью плоских диаграмм — не единственная
возможность. Рядом с теорией узлов стоит другая важная теория —
теория кос . Существуют четыре классических определения группы кос.
Косы связаны с такими красивыми алгебраическими объектами, как
полиномы комплексного переменного без кратных корней. Под косой
из п нитей понимают набор из п попарно непересекающихся
восходящих кривых, соединяющих точки А\,...,АП на одной прямой
с точками Bi,...,Sn на параллельной ей прямой. Аналогично
диаграммам узлов задаются диаграммы кос, при этом эквивалентность кос
определяется как такая изотопия, в каждый момент которой дуги
должны быть восходящими. Произведение кос а и Ь получается с помощью
пристраивания нижних вершин косы а к верхним вершинам косы Ь.

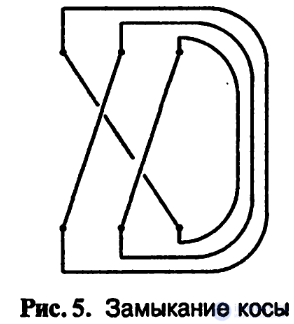
Легко видеть, что замыкая косу, т.е. соединяя самым простым
образом Ai с В{} i = 1,..., п, как это показано на рис. 5, мы получим
диаграмму узла или зацепления.

В книге описываются три важные теоремы, связанные с косами.
Теорема Александера (см., например, [123]) утверждает, что каждый
изотопический класс узла или зацепления может быть получен
замыканием косы, теорема Артина (см. [5]) о представлении групп кос
с помощью образующих и соотношений и теорема Маркова [66] о
движениях кос, оставляющих без изменения изотопический класс узла.
На теореме Маркова основан и алгоритм Деорнуа, распознающий изо-
топность кос; этому алгоритму будет посвящена отдельная лекция. При
этом выгодное отличие теории кос заключается в том, что она —
алгебраическая, т. е. каждый узел может быть записан в виде слова (вообще
говоря, в бесконечном алфавите).
Из литературы, охватывающей все описанное выше, я рекомендую
две книги Луиса Кауфмана [47, 48], а также книги Дж. Адамса [1],
А. Каваучи [52] и (на русском языке) [94].
Предположим, что у нас есть узел и мы хотим изменить его
изотопический класс, гладко изменяя отображение окружности в R3. Без
пересечения этого сделать нельзя, поэтому самым важным является
момент пересечения. Если при таком отображении пересечение ровно
одно, в нем участвуют ровно две ветви узла и пересекаются трансвер-
сально, то такое отображение окружности в R3 называется сингулярным
узлом. Пространство сингулярных узлов называется дискриминантным
пространством.
Изучая свойства дискриминантов, В. А. Васильев ввел понятие
инвариантов конечного порядка, впоследствии получившее название
инвариантов Васильева. Изначально инварианты Васильева требовали
большого неэлементарного математического аппарата, однако
впоследствии была найдена их простая комбинаторная интерпретация, о
которой будет рассказано позднее. Далее будет также доказано, что
инварианты Васильева сильнее всех вышеперечисленных полиномиальных
инвариантов.
Изначально доказательство существования инвариантов Васильева
появилось в работе [85]; структура этих инвариантов (только для узлов)
была получена М. Л. Концевичем с помощью замечательной
конструкции знаменитого интеграла, носящего его имя. В первых версиях работы
Концевича (до публикации) была обнаружена ошибка, о чем ему
сообщил Д. Бар-Натан, после чего Концевич свою работу исправил. Эту
работу можно прочесть в [56]. При этом мы предлагаем изучать
конструкцию интеграла Концевича по статье [13]. В [13] изучены алгебры
хордовых и китайских диаграмм, а также их связь с инвариантами
представлений алгебр Ли.
Вычисление интеграла Концевича долгое время было очень
трудным делом до того, как появилась работа Ле и Мураками [63], в которой

они, по сути дела, представляют технику такого вычисления. Она,
однако, весьма сложная, и мы ею заниматься не будем.
Есть еще один красивый способ представления всех узлов и
зацеплений, он основан на введенном в [107] понятии d-диаграммы —
окружности с двумя семействами непересекающихся хорд, ^-диаграммам
посвящена четвертая глава настоящей книги. Эта теория происходит
из теории атомов и гамильтоновых систем и позволяет построить
скобочную полугруппу узлов, описав, тем самым, все узлы и зацепления
в виде слов в конечном алфавите из четырех букв, см. [107]. В этом
состоит превосходство кодирования с помощью d-диаграмм, например,
над кодированием с помощью кос, требующим бесконечный набор
букв. Кроме того, этот способ просто и красиво обобщается на случай
сингулярных узлов, что позволяет дать описание инвариантов Васильева
в виде слов в конечном алфавите.
С помощью d-диаграмм все узлы и зацепления представляются
в виде петель на клетчатой бумаге, исходящих из начала координат
и лежащих внутри первого квадранта.

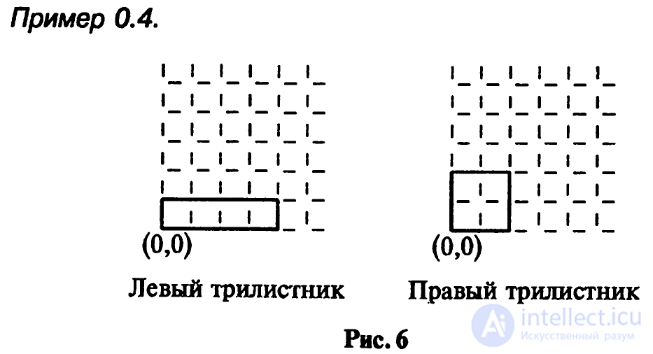
Левый трилистник может быть записан как прямоугольник 1x4, правый —
как квадрат 2x2, см. рис. 6.
Вообще, теория атомов, изначально изобретенная для
классификации гамильтоновых систем, оказывается применимой во
многих областях геометрии и топологии, например, для кодирования 3-
многообразий.
Упомяну в конце введенное Луисом Кауфманом в 1996 году
понятие виртуального узла — комбинаторное понятие, основанное на
диаграмме узла. Теория виртуальных узлов может быть интерпретирована
как «проекция» теории узлов в различных трехмерных
многообразиях. Эта теория бурно развивается и имеет много общего в подходах
с классической теорией узлов.

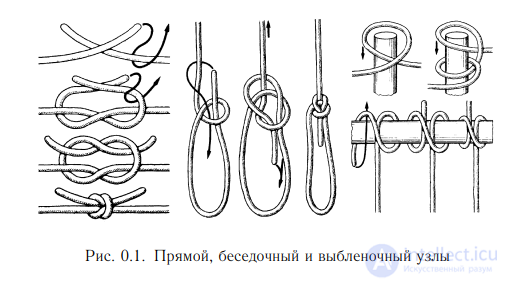
Узлы повсеместно использовались уже со времен античности. Это объясняется их важной технологической ролью, особенно в мореходстве и строительстве. Но появление веревок и узлов произошло раньше, в доисторические времена, и предшествовало изобретению топора, лука, колеса. Сегодня мы применяем узлы, не задумываясь даже, что их возраст исчисляется тысячелетиями. Нам и в голову не приходит, что такие узлы, как выбленочный, прямой и беседочный (см. рис. 0.1), служили жите ´ - лям Древнего Египта еще пять тысячелетий назад. (Например, выбленочный узел был обнаружен на двери третьего помещения гробницы фараона Тутанхамона.)

Прямой (или квадратный) узел, хорошо известный в Древнем Египте, был широко распространен в быту древних греков и римлян. Он украшал жезл древнеримского бога Меркурия — покровителя торговли — и назывался nodus Hercules — геркулесовым узлом, так как этот древний герой носил шкуру убитого льва, передние лапы которого связывал на груди именно так.

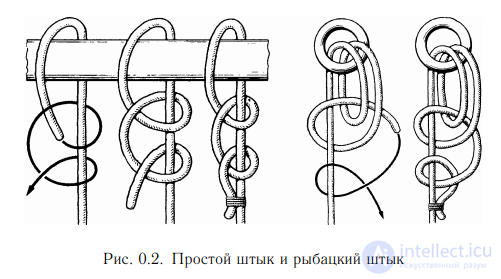
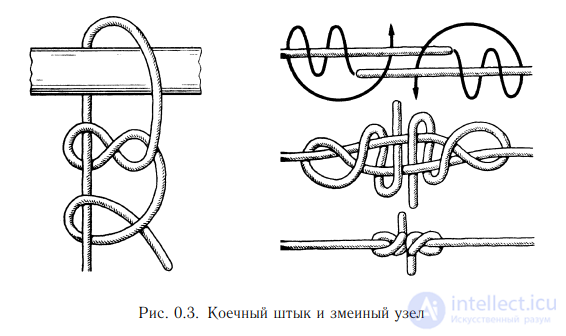
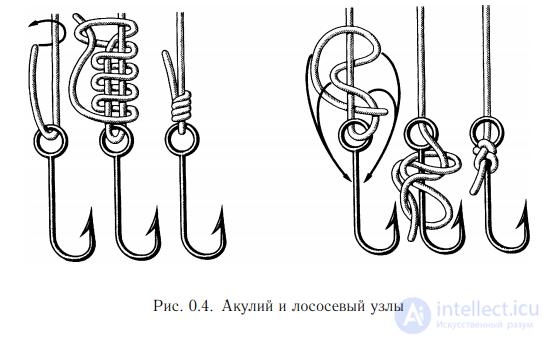
Изобретателями самых хитроумных и надежных узлов оказались моряки. Ведь именно им, чаще, чем постоянным обитателям суши, приходилось иметь дело с веревками и канатами. Лучшие из узлов пережили века, переходя от поколения к поколению (см. Adams, 1994, где приведены изображения более 700 различных узлов). Здесь мы рассмотрим лишь несколько примеров узлов. Так, простой штык применяется для подъема грузов; рыбацкий штык (или якорный узел) признан моряками всех стран как самый надежный для прикрепления каната к якорю (рис. 0.2). Коечный штык применяется для крепления подвесных коек на судах; змеиным узлом можно накрепко связать две рыболовные снасти (рис. 0.3). На рис. 0.4 изображены два из многочисленных рыболовных узлов: акулий и лососевый.

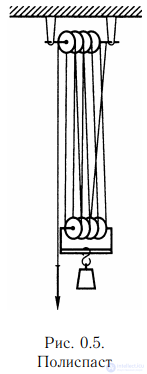
Одним из первых авторов сочинений про узлы был англичанин Джон Смит (John Smith), известный каждому американскому школьнику своими романтическими приключениями с прекрасной индейской принцессой Покахонтас, столь трагически для нее окончившимися. В 1627 г. он издал морской словарь, где описал некоторые узлы. Столетием позже узлы становятся объектом детальной статьи в «Энциклопедии» Дидро и Даламбера. Много специальных узлов связано с одним из главных технологических изобретений древности — блоком. На рис. 0.5 изображен полиспаст, своего рода канатный рычаг Архимеда. Это устройство соединяет в себе два великих изобретения — колесо и канат — и применяется для подъема грузов. Наряду с технологическими и практическими применениями, несомненно, нужно упомянуть также эстетический и магический аспекты. Скандинавские народы (возможно, в силу своей неразрывной связи с морем) особенно любили украшения в виде узлов (рис. 0.6). Их часто помещали на оружие, форштевни кораблей (рис. 0.7), применяли для создания узоров

Одно из наиболее ярких применений узлов можно увидеть в орнаментах болгарских, новгородских и московских летописей XII–XIV вв. (рис. 0.8).

Сегодня мы находимся в положении, близком к сложившемуся в 1860 г.: многие исследователи полагают, как полагал в свое время Уильям Томсон, что узлы играют ключевую роль в фундаментальной физической теории, описывающей структуру материи. Однако это не возвращение к начальной точке — спираль познания совершила полный виток, и мы обнаруживаем себя в том же положении, но на более высоком уровне.

Теория узлов остается живой и загадочной. Главные проблемы по-прежнему открыты: узлы продолжают ускользать от попыток их ясно классифицировать, и по-прежнему неизвестно, обладают ли они легко вычислимой полной системой инвариантов. И наконец, та фундаментальная роль, которую, как полагают, они играют в физике, еще до конца не определилась

Исследование, описанное в статье про теория узлов, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое теория узлов, теория кос и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теории узлов, зацеплений, кос и их инвариантов