§ 2. Арифметика узлов и поверхности Зейферта кратко

Привет, Вы узнаете о том , что такое § 2. Арифметика узлов и поверхности Зейферта, Разберем основные их виды и особенности использования. Еще будет много подробных примеров и описаний. Для того чтобы лучше понимать что такое § 2. Арифметика узлов и поверхности Зейферта , настоятельно рекомендую прочитать все из категории Теории узлов, зацеплений, кос и их инвариантов.

Поговорим теперь о структуре, возникающей на пространстве узлов.

Пусть даны два ориентированных узла К₁ и К₂.
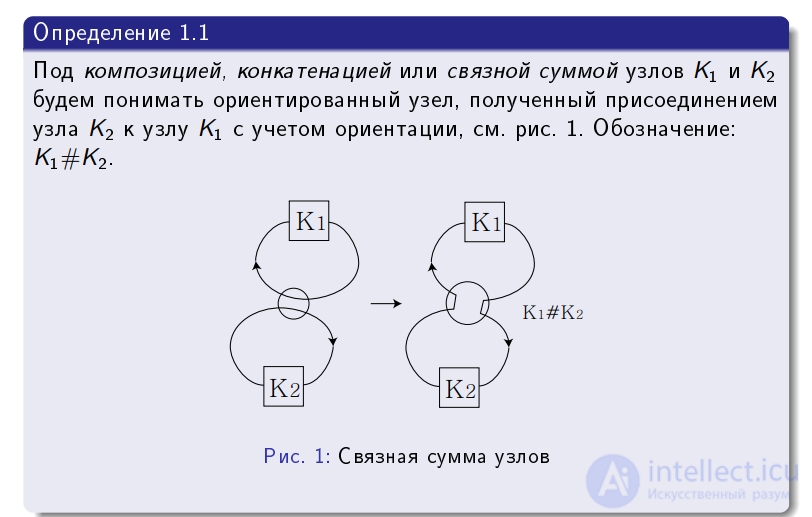
Определение 1.6. Композицией или связной суммой узлов К₁ и К₂. называют ориентированный узел, полученный естественной операцией приклеивания узла К2 к узлу К1 с учетом ориентации, см. рис. 5. Связную сумму обозначают через К1#К2-

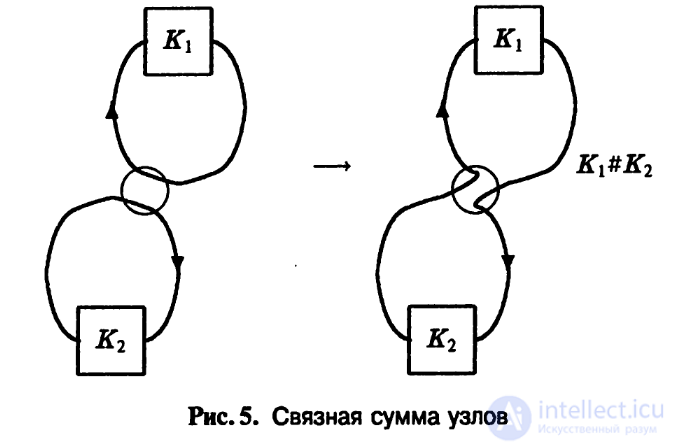
Упражнение 1.6. Покажите, что изотопический класс полученного узла
не зависит от выбора того участка, на котором узлы подходят друг к другу.

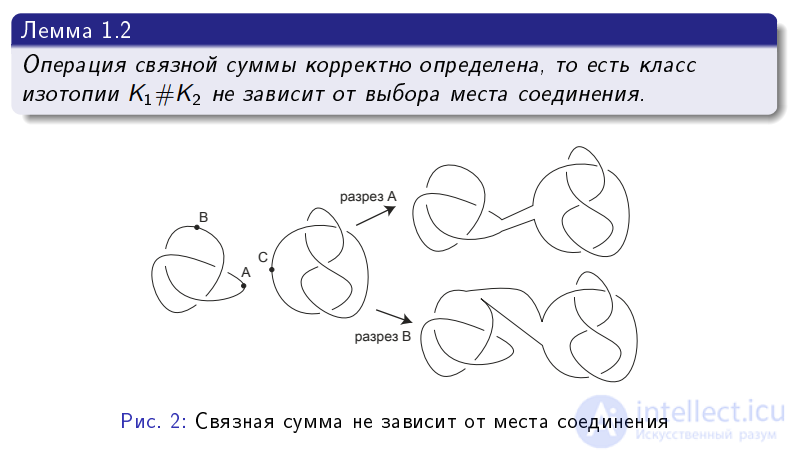
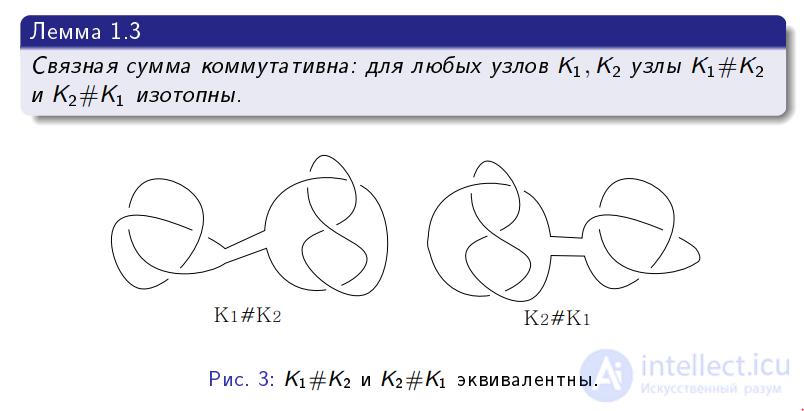
Упражнение 1.7. Докажите, что операция конкатенации на узлах коммутативна, т.е. для каждых двух узлов jfiTj, JiT2 узлы К^К2 и К2#Ку изотопны.
Более того, можно провести такую изотопию и на бесконечных (длинных) R3, оба конца которого уходят узлах, т. е. на отображениях интервала в на бесконечность.
Тогда для каждого

Теорема 1.2. Пусть узел К1 нетривиальный, узла К2 узел К1#К2 также нетривиальный.
Доказательство. Рассмотрим последовательность узлов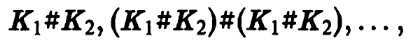
в которой первый узел К у лежит внутри шара радиуса 1, узел К2, следующий за ним, лежит внутри круга радиуса \, следующий узел К$ —
внутри круга радиуса |,ит.д. Тогда на ограниченном множестве можно
уместить всю бесконечную последовательность узлов, см. рис. 6.

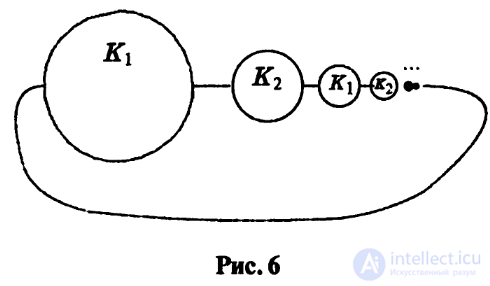
Получим узел, который, возможно, будет диким, и назовем его а.
Так как K1#K2 — тривиальный узел, то узел о — также тривиальный.

С другой стороны, 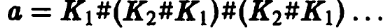В силу того, что
операция связной суммы на узлах коммутативна, узел К2#K1 — тривиален.
Следовательно, узел а изотопен K1, что противоречит предположению
о нетривиальности K1. Теорема доказана. ■

Определение 1.7. Узел К называется простым, если не существует нетривиальных узлов Ly M, таких, что К = L#M. Остальные узлы называются составными.

Определение 1.8- Если для узлов J5T, X, М справедливо утверждение К = £#М, то говорят, что узлы L, М делят К. Итак, мы установили, что в полугруппе узлов все элементы, кроме
тривиального, не имеют обратных элементов. Какими еще свойствами обладают узлы?

Упражнение 1.8. Покажите, что любой узел вкладывается в некоторую сферу с g ручками, точнее, любой изотопический класс узла может быть получен в виде кривой на некоторой сфере с ручками, стандартно вложенной в R3.

Замечание 1.5. То же утверждение верно и для зацеплений. В силу известной теоремы Жордана понятно, что в сферу (без ручек) вкладывается лишь тривиальный узел.
Дадим теперь определение поверхности Зейферта узла [121, 104].

Определение 1.9. Пусть L — ориентированное зацепление. Поверхностью Зейферта зацепления L называют связную компактную ориентированную двумерную поверхность в 53, краем которой
служит зацепление L, причем ориентация L индуцирована ориентацией поверхности.

Теорема 1.3. У любого зацепления в R3 существует поверхность Зейферта. Доказательство. Рассмотрим плоскую диаграмму D зацепления L. Будем уничтожать перекрестки узла, как это показано на рис. Об этом говорит сайт https://intellect.icu . 7.
После уничтожения получится набор замкнутых непересекающихся простых кривых на плоскости. Эти кривые называются окружностями Зейферта. Заклеим эти окружности дисками в трехмерном пространстве. Хотя внутренности этих окружностей на плоскости могут содержаться одна в другой, диски в трехмерном пространстве можно расположить непересекающимися, приподняв внутренние точки над
плоскостью диаграммы.
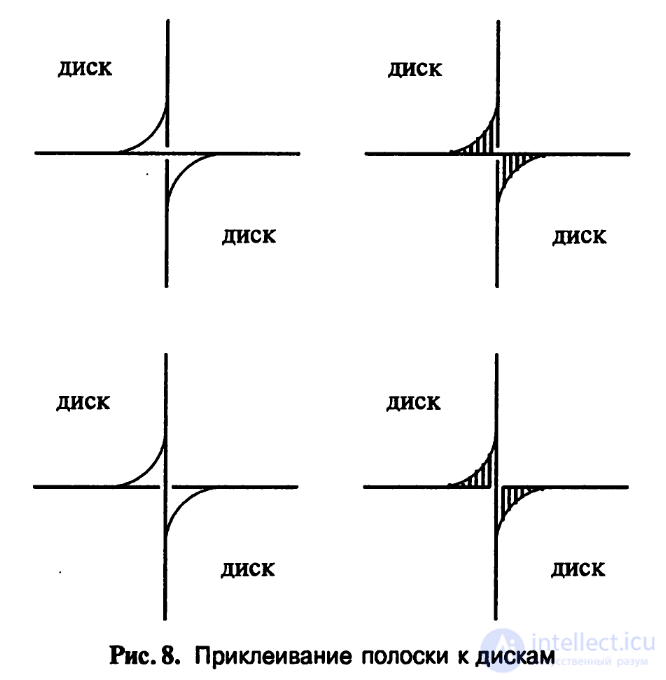
В окрестности каждого перекрестка друг к другу подходят два Диска. Выберем два отрезка на краях этих дисков и соединим диски перекрученной полоской, краями которой служат ветви зацепления, инцидентные этому перекрестку, см. рис. 8. На рис. 8 сверху и снизу лента перекручивается в разные стороны, при этом в одном случае вертикальная ветвь расположена выше горизонтальной, а во втором — наоборот.

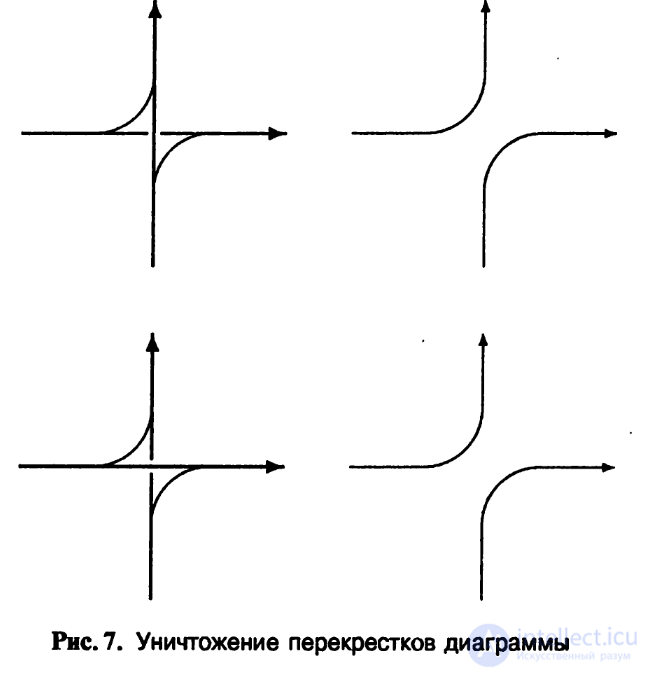
Рис. 7. Уничтожение перекрестков диаграммы

Получим некоторую (не обязательно связную) поверхность. Соединяя связные компоненты этой поверхности тонкими трубками, будем уменьшать число связных компонент, пока оно не станет равным единице. ■

Осталось показать, что полученная поверхность является ориентируемой. Действительно, рассмотрим плоскость, на которой расположена поверхность узла и выберем на ней положительный репер. Он порождает ориентацию для каждого диска, заклеивающего окружность Зейферта. При этом для двух окружностей Зейферта, примыкающих к одной вершине, такие ориентации являются противоположными (в смысле поверхности Зейферта), так как между ними приклеена перекрученная лента. Осталось показать, что любая последовательность 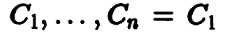окружностей Зейферта, в которой любые две окружности 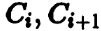имеют общую вершину, имеет нечетную длину (т. е. п — нечетно), т. е. что из любой области можно добраться до нее самой, совершив лишь четное число перекручиваний, т. е. пройдя лишь четное количество перекрученных лент. Это следует из того, что у многоугольника с нечетным числом сторон нельзя выбрать
ориентацию сторон так, чтобы ориентации любых двух соседних сторон были
противонаправлены.

Теорема 1 -4. Четность количества окружностей поверхности Зейферта, построенной по диаграмме к-компонентного зацепления с п пересечениями, совпадает с четностью числа п — к.
Доказательство. Пусть L — диаграмма к -компонентного
зацепления с п вершинами. Устроим разбиение поверхности Зейферта на клетки следующим образом. Выберем сначала одномерный остов, в котором вершинами являются перекрестки диаграммы L, а ребрами — ребра этой диаграммы. Количество клеток такого разбиения поверхности равно количеству окружностей Зейферта — каждая клетка заклеивает одну окружность Зейферта. Если теперь заклеить граничные окружности (т. е. компоненты зацепления) дисками, мы получим ориентированное Двумерное многообразие без края, так как поверхность Зейферта была ориентируемой. Эйлерова характеристика этого многообразия должна быть четной. Она равна п - 2п + S + к, где 2п — количество ребер диаграммы L, S — количество окружностей Зейферта. Учитывая четностьчисла -n + S + к, получаем требуемое.

Поверхность Зейферта узла К представляет собой компактную двумерную поверхность, краем которой служит одна заузленная
окружность (сам узел К). Приклеивая к этой окружности диск, получим сферу с некоторым количеством д ручек.

Определение 1.10. Говорят, что узел К является узлом рода д, если д — минимальное количество ручек заклеенной поверхности Зейферта узла К.

Замечание 1.6. На самом деле, проблема вычисления рода узла — очень сложная, она была решена Хаксном (см. [40]), в частности, из ее решения следует решение проблемы распознавания тривиального узла (узла рода 0) с помощью алгоритма Хакена.

Лемма 1.1. Функция д является аддитивной, т.е. для любых двух узлов K1УК2 верно равенство д(К{) + д(К2) = g(Ki#K2).
Доказательство. Покажем сначала, что д(K1#К2) ^ д(K1) + 0(^2)-
Рассмотрим поверхности Зейферта F\ и F2 минимальных родов
узлов К{ и К2. Без ограничения общности можно считать, что эти
поверхности не пересекаются. Два малых участка краев этих
поверхностей соединим полосой так, чтобы соблюдалось условие
ориентации. В результате получится поверхность Зейферта узла K1#К2 рода
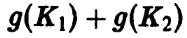. Отсюда
.
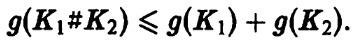Покажем теперь, что 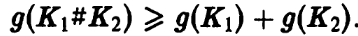- Рассмотрим
поверхность Зейферта F минимального рода узла K1#К2. Существует
(топологическая) сфера S2, разделяющая узлы K1 и К2 в K1#К2.
Сфера S2 пересекает F по набору замкнутых кривых
(топологических окружностей) и кривой с концами в точках А, В. Каждая
окружность делит сферу S2 на две части, одна из которых не содержит
кривой АВ. Окрестность пересечения F и S2 около каждой
окружности имеет вид цилиндра, протыкающего поверхность сферы и не
содержащего кривой АВ. Удалим из такого цилиндра его малую
цилиндрическую часть, содержащую окружность, и заклеим двумя дисками
оставшиеся части цилиндра. Если получившаяся поверхность окажется
несвязной, то возьмем ту ее часть, которая содержит узел K1#К2.
Сделав такие операции применительно к каждой окружности, получаем
замкнутую поверхность F1, содержащую узел K1#К2 и пересекающую 52
только по дуге АВ. При указанных операциях количество ручек на ка-
ркдом шаге не увеличивалось. Следовательно,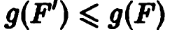 Поскольку
род поверхности F минимален, то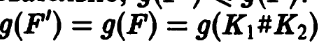

Сфера 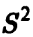разбивает поверхность F1 на поверхности Зейферта для
узлов К{ и К2. Следовательно,

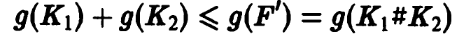
Ч.Т.Д. ■
Из аддитивности рода узла легко следует, что у нетривиального узла не может быть обратного, так как тривиальный узел имеет род ноль, а все остальные узлы имеют род, больший нуля.

Упражнение 1.9. Покажите, что трилистник имеет род один и является простым узлом.
Следовательно, каждый узел разлагается не более, чем на конечное число простых множителей.
Для полного прояснения картины относительно арифметики узлов нам осталось доказать еще одну лемму — об однозначном разложенииузла на множители.

Лемма 1.2. Пусть L u M — умы, а К — простой узел, делящий L#M. Тогда либо К делит L, либо К делит М.
Доказательство. Рассмотрим узел L#M и плоскость р, пересекающую этот узел в двух точках и отделяющую L orr М. Так как ЫМ делится на К, то найдется двумерная сфера S2 (в топологическом
смысле), пересекающая L#M в двух точках и содержащая узел К внутри себя. Если бы наша сфера не пересекала плоскости р, задача была бы решена. В противном случае сфера S2 пересекает плоскость по некоторому числу несамопересекающихся окружностей. Если эти окружности (как узлы) незацеплены с L#M, то деформацией сферы они легко убираются. В противном случае их также можно убрать с помощью деформации сферы в силу простоты узла К (так как узел простой, то внутри сферы по крайней мере с одной стороны от плоскости может находиться лишь тривиальная его часть).
Следовательно, если узел L#M делит К, то один из узлов L или М делит К, ч.т.д. ■
Таким образом, мы имеем:

• а) Изотопические классы узлов образуют коммутативную полугруппус единицей относительно операции связной суммы; единицей этой полугруппы является тривиальный узел.
• б) Любой нетривиальный узел не имеет обратного в данной полугруппе.
• в) Разложение на простые множители в полугруппе узлов единственно.
• г) Количество различных простых узлов счетно.

Последнее утверждение остается читателю в качестве упражнения. Так как изотопических классов гладких узлов счетное число (докажите это!), мы получаем теорему.

Теорема 1.5. Полугруппа изотопических классов узлов относительно операции взятия связной суммы изоморфна полугруппе натуральных чисел по умножению. При этом простым узлам соответствуют простые числа.
При этом описанный изоморфизм — не канонический, поскольку на множестве узлов нет канонического линейного порядка, т. е. нельзя, например, сказать, соответствует ли простой узел трилистник простому числу три или простому числу семнадцать.
Счетная полугруппа, обладающая свойствами а)-г), единственна с точностью до изоморфизма, поэтому все такие полугруппы некоторымобразом «связаны» с узлами.
В [107] приведено чисто алгебраическое описание этой полугруппы, т. е. приведен явный (конструктивный) изоморфизм этой геометрической полугруппы и чисто алгебраически заданной полугруппы.

Исследование, описанное в статье про § 2. Арифметика узлов и поверхности Зейферта, подчеркивает ее значимость в современном мире. Надеюсь, что теперь ты понял что такое § 2. Арифметика узлов и поверхности Зейферта и для чего все это нужно, а если не понял, или есть замечания, то не стесняйся, пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Теории узлов, зацеплений, кос и их инвариантов