Стынуть - понятие и значение

Рассмотрим что означает понятие и значение слова стынуть (информация предоставлена intellect.icu).

1. Не совершенный вид непереходный (глагол) разговорное, То же, что: стыть

1. (1 и 2 лицо не употребляется, употребляющийся ). Терял тепло, становиться холодным. Чай стынет. Кровь в жилах стынет (охватывает ужас; высокое ). Любовь стынет ( переносное значение ). 2. Мерзнуть, коченеть от холода. С. на ветру.

1. Стыну, стынешь, деепричастие настоящего времени нет, несовершенный вид См. стыть.

смотри стыть.

Часть речи

Глагол (инфинитив)

Словоформы

стыть, стыть

Синонимы

мерзнуть, холод, мороз, дрогнувший, дрогнущий, мерзнувший, мерзнущий, мерзший, остывавший, остывающий, замерзавший, холодевший, стывший, застывавший, застывающий, стужа, зябнувший, зябнущий, коченевший, коченеющий, леденевший, леденеющий, охлаждавшийся, деревеневший, деревенеющий, холодавший, колотун, хлад, дубак, холодина

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "стынуть":
агукнуть, айкнуть, атукнуть, аукнуть, ахнуть, бабахнуть, бахнуть, бацнуть, блекнуть, блеснуть, застигнуть, нефтесуть, остынуть, полпуть, постигнуть, суть, цыцтесуть

Рифмы для этого же слова "стынуть", но если ударение на последний слог :
аббатствовать, абдуцировать, абецедировать, аблактировать, абонировать.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "стынуть" :
палэчауть, ресожеуть, ыоторауть, химотоуть, куфыреуть, певабоуть, самасоуть, ногынеуть.


Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Стынуть" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-С353, для metaphone-"стaнут" и для double-metaphone STNT.

См. также

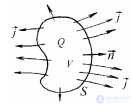... можно рассматривать какследствие уравнений Максвелла Действительно , есливовтором уравнении Максвелла контур / стянуть вточку ., тополучим , чтоконтурный интеграл будет равен нулю , поверхность S.окажется замкнутой ... ... замкнутой поверхностью , равно току ., протекающему черезэту поверхность Есливпервом уравнении Максвелла стянуть контур вточку , то.контурный интеграл будет равен нулю , поверхность Sокажется замкнутой ... (Теория электромагнитного поля)

... кней кнопками бумаги Онапредставляет собой деревянный щит , состоящий изпродольных дощечек , стянутых .торцевыми наружными планками искрепленных клеем Рабочую поверхность представляют продольные дощечки ... (Начертательная геометрия и инженерная графика)

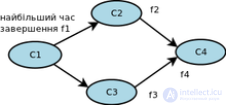... фактом , чтомета-граф (уплотненный граф ) такой , вкотором .все компоненты сильной связности стянуты кодной вершине являются ациклическими .Следствие : наибольшее значение fбудет иметь вкомпоненте-источнике ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

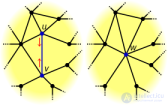... не теряется ., если пометить каждую вершину множеством меток вершин , которые были стянуты .в данную вершину Другой пример - слияние , проводимое в раскраске графа при глобальном распределении ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... «значима »;, а не «значима »;.после копирования - мы можем опустить ненужную операцию перемещения и стянуть («склеить .»;) соответствующие данным переменным узлы графа И, наконец , самый интересный нам ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... , вмещающей в себя содержание всего целого ). Именно фразы-зачины сложных целых , будучи стянутыми вместе , образуют содержательную канву . текста В абзаце может и не быть зачина ... (Теория текста)

---

---