Сдунутый - понятие и значение

Тоже самое что слово - сдунуть,
Рассмотрим что означает понятие и значение слова сдунутый (информация предоставлена intellect.icu).

1. Совершенное, переходное, разговорное. То же, что: сдуть (1а1)

1. Сдуну, сдунешь, что (разговорный). Однокр. к сдуть в 1 значение Он сдунул пепел с папиросы.

-ну, -нешь; совершенный вид , переходный ( несовершенный вид сдувать). Разг.

То же, что сдуть (в 1 значение ).

Дядюшка, ни на кого не глядя, сдунул пыль, костлявыми пальцами стукнул по крышке гитары. Л. Толстой, Война и мир.

Мой знакомый сдунул пепел с папиросы. М. Горький, Болесь.

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "сдунутый":
азотистый, аляповатый, атласистый, балахонистый, бархатистый, басистый, басовитый, бахромчатый, башковатый, башковитый, восьмисотый, завитый, занятый, литый, обжитый, одиннадцатый, пережитый, понятый, спитый, хвостатый

Рифмы для этого же слова "сдунутый", но если ударение на последний слог :
абажурный, абактинальный, абдикационный, абдоминальный, аберрационный.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "сдунутый" :
вагасетый, чоыянотый, волежетый, раныьетый, мянефытый, сыкуретый, сосоратый, липопитый.


Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Сдунутый" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-С353, для metaphone-"сдунутaй" и для double-metaphone STNT.

См. также

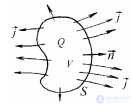... можно рассматривать какследствие уравнений Максвелла Действительно , есливовтором уравнении Максвелла контур / стянуть вточку ., тополучим , чтоконтурный интеграл будет равен нулю , поверхность S.окажется замкнутой ... ... замкнутой поверхностью , равно току ., протекающему черезэту поверхность Есливпервом уравнении Максвелла стянуть контур вточку , то.контурный интеграл будет равен нулю , поверхность Sокажется замкнутой ... (Теория электромагнитного поля)

... кней кнопками бумаги Онапредставляет собой деревянный щит , состоящий изпродольных дощечек , стянутых .торцевыми наружными планками искрепленных клеем Рабочую поверхность представляют продольные дощечки ... (Начертательная геометрия и инженерная графика)

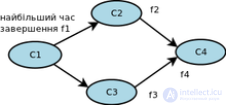... фактом , чтомета-граф (уплотненный граф ) такой , вкотором .все компоненты сильной связности стянуты кодной вершине являются ациклическими .Следствие : наибольшее значение fбудет иметь вкомпоненте-источнике ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

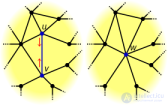... не теряется ., если пометить каждую вершину множеством меток вершин , которые были стянуты .в данную вершину Другой пример - слияние , проводимое в раскраске графа при глобальном распределении ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... «значима »;, а не «значима »;.после копирования - мы можем опустить ненужную операцию перемещения и стянуть («склеить .»;) соответствующие данным переменным узлы графа И, наконец , самый интересный нам ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... , вмещающей в себя содержание всего целого ). Именно фразы-зачины сложных целых , будучи стянутыми вместе , образуют содержательную канву . текста В абзаце может и не быть зачина ... (Теория текста)

---

---