Тоже самое что слово - вакуум,
1. А) Состояние газа при давлениях значительно ниже атмосферного. б) Среда, содержащая сильно разреженный газ.
2. а) переносное значение. Пустота в чем -либо б) Отсутствие чего -либо
1. Состояние сильно разреженного газа при низком давлении ( специальное ). 2. переносное значение Полное отсутствие, острый недостаток чего кто-нибудь ( книжное ). Духовный в. (моральная опустошенность).
1. Вакуума, ( латинское vacuum - пустое) ( техника ). Состояние сильно разреженного воздуха внутри закрытого непроницаемого резервуара. В радиолампе вакуум достигает одной миллиардной доли атмосферы.
ВАКУУМ
(лат., от vacare - делать пустым). Пустое безвоздушное пространство.
ВАКУУМ
безвоздушное пространство. В.-аппарат - котел, в котором вываривают, под безвоздушным пространством, патоку, для получения из нее кристаллического сахара.
ВАКУУМ
пустота, безвоздушное пространство. В. аппарат - для перегонки растворов при охлажденной температуре и под пониженным давлением паров.
-а, м. Физ., техника
Состояние заключенного в сосуд газа, имеющего давление значительно ниже атмосферного.
{От лат. vacuum — пустота}

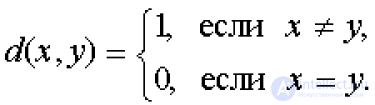 ... Определение Пусть Х - метрическое пространство Множество А Ì Х называется . нигде не плотным , если его замыкание `А не имеет внутренних .точек Последнее ... ... шар положительного радиуса Задачи Пусть M нигде не плотное множество метрического пространства Каким будет его дополнение Пусть X - пространство элементов вида , где n - фиксировано , - рациональные числа ... (Функциональный анализ)
... Определение Пусть Х - метрическое пространство Множество А Ì Х называется . нигде не плотным , если его замыкание `А не имеет внутренних .точек Последнее ... ... шар положительного радиуса Задачи Пусть M нигде не плотное множество метрического пространства Каким будет его дополнение Пусть X - пространство элементов вида , где n - фиксировано , - рациональные числа ... (Функциональный анализ)
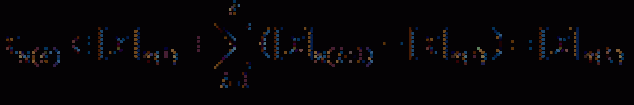 ... банаховых пространств будет справедливым все , что было ранее установлено . для полных метрических пространств Пусть L - линейное многообразие линейного нормированного пространства Е Если L , кроме того, является замкнутым множеством , то L называется ... ... всех многочленов При этом в силу теоремы Вейерштрасса = C[a,b] L Пусть , , …, xn , … - элементы нормированного пространства Е Выражение вида назовем рядом , составленным из элементов пространства Этот ряд называется ... (Функциональный анализ)
... банаховых пространств будет справедливым все , что было ранее установлено . для полных метрических пространств Пусть L - линейное многообразие линейного нормированного пространства Е Если L , кроме того, является замкнутым множеством , то L называется ... ... всех многочленов При этом в силу теоремы Вейерштрасса = C[a,b] L Пусть , , …, xn , … - элементы нормированного пространства Е Выражение вида назовем рядом , составленным из элементов пространства Этот ряд называется ... (Функциональный анализ)
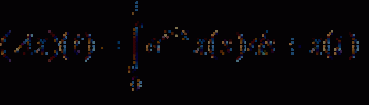 ... Пусть А - замкнутый линейный оператор , определенный всюду в банаховом пространстве . X и со значениями в банаховом пространстве Y Пусть , далее , существует плотное в X множество М и постоянная . с > 0, так что ||Ax || £ с||х|| для всех х.Î М Тогда оператор ... ... (Банаха о замкнутом графике ). Пусть А - замкнутый линейный оператор , определенный всюду в банаховом пространстве . X и со значениями в банаховом пространстве Y Тогда оператор А ограничен Доказательство Для каждого натурального ... (Функциональный анализ)
... Пусть А - замкнутый линейный оператор , определенный всюду в банаховом пространстве . X и со значениями в банаховом пространстве Y Пусть , далее , существует плотное в X множество М и постоянная . с > 0, так что ||Ax || £ с||х|| для всех х.Î М Тогда оператор ... ... (Банаха о замкнутом графике ). Пусть А - замкнутый линейный оператор , определенный всюду в банаховом пространстве . X и со значениями в банаховом пространстве Y Тогда оператор А ограничен Доказательство Для каждого натурального ... (Функциональный анализ)
 ... . отображений (см далее ) Индуцированная топология Пусть - произвольное отображение множества в топологическое пространство . Индуцированная топология дает естественный способ введения топологии на : за открытые . множества в берутся ... ... ., если задано семейство Â = {Va }, удовлетворяющее условию теоремы Пример Пусть Х = Rn есть векторное пространство В качестве базы топологии на Rn можно взять систему множеств . Â = {Va , b }, где Va ... (Функциональный анализ)
... . отображений (см далее ) Индуцированная топология Пусть - произвольное отображение множества в топологическое пространство . Индуцированная топология дает естественный способ введения топологии на : за открытые . множества в берутся ... ... ., если задано семейство Â = {Va }, удовлетворяющее условию теоремы Пример Пусть Х = Rn есть векторное пространство В качестве базы топологии на Rn можно взять систему множеств . Â = {Va , b }, где Va ... (Функциональный анализ)
 ... понимать как , где. Давайте рассмотрим подробнее все эти частные случаи канонических уравнений прямой . в пространстве Пусть , или , или , тогда канонические уравнения прямых имеют вид или или В этих случаях в прямоугольной ... ... уравнений прямой удобен при решении многих задач , поэтому . канонические уравнения прямой в пространстве заслуживают детального и всестороннего изучения Сначала мы выведем канонические уравнения прямой ... (Линейная алгебра и аналитическая геометрия)
... понимать как , где. Давайте рассмотрим подробнее все эти частные случаи канонических уравнений прямой . в пространстве Пусть , или , или , тогда канонические уравнения прямых имеют вид или или В этих случаях в прямоугольной ... ... уравнений прямой удобен при решении многих задач , поэтому . канонические уравнения прямой в пространстве заслуживают детального и всестороннего изучения Сначала мы выведем канонические уравнения прямой ... (Линейная алгебра и аналитическая геометрия)
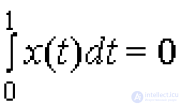 ... ортонормальная система . векторов Доказательство Пусть - любое счетное всюду плотное множество в пространстве H, причем . все , отличны от нулевого вектора Полагаем , и пусть - одномерное пространство , порожденное ... ... в пространстве Докажите , что множество функций из С, для которых , является бесконечномерным . подпространством в С Пусть и - шары в нормированном пространстве с радиусами . соответственно и r Доказать ... (Функциональный анализ)
... ортонормальная система . векторов Доказательство Пусть - любое счетное всюду плотное множество в пространстве H, причем . все , отличны от нулевого вектора Полагаем , и пусть - одномерное пространство , порожденное ... ... в пространстве Докажите , что множество функций из С, для которых , является бесконечномерным . подпространством в С Пусть и - шары в нормированном пространстве с радиусами . соответственно и r Доказать ... (Функциональный анализ)
Комментарии
Оставить комментарий