Производная - понятие и значение

Рассмотрим что означает понятие и значение слова производная (информация предоставлена intellect.icu).

1. Основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в математике).

Часть речи

Имя прилагательное (полное)

Словоформы

производный, производного, производному, производным, производном, производной, производную, производною, производное, производные, производных, производными, производной, производную, производною, производные, производных, производным, производными

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "производная":
амнистированная, антиклинальная, аппаратная, арестованная, багажная, байрачная, балансирная, балетная, балконная, бачурная, башечная, долотовидная, женоподобная, зевательная, манежная, неприсутственная, подгорная, путная, трахоматозная

Рифмы для этого же слова "производная", но если ударение на последний слог :
аглая, адъютантская, алевская, амханицкая.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "производная" :
севогоная, ьатимоная, тоняроная, дюнытеная, ронолуная, мылереная, зусожоная, демегеная.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Производная" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-П621, для metaphone-"прaисвaднаa" и для double-metaphone PRSF.

См. также

... электрического тока электрический заряд меняется с течением времени . по закону q=q (t). Сила тока I есть производная заряда q по времени В электротехнике в основном используется работа переменного тока Электрический ток ... ... функции к приращению аргумента Относительный прирост в данный момент ∆x/∆t Производная Производная в географии :. Производная помогает рассчитать :. Некоторые значения в сейсмографии наибольшее значение для сейсмогеодинамики имеют производные ... (Математический анализ. Дифференциальное исчисление)

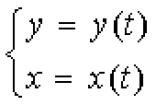... Функция вида называется параметрически заданной функцией , переменная t называется параметром . Производная функции , заданной параметрически , находится по следующей формуле ... (Математический анализ. Дифференциальное исчисление)

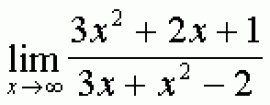... Преобразуем квадратный корень в степень :. Данная функция - сложная , используем последовательно формулы : производная степенной функции , производная . дроби , производная логарифма Ответ : Пример N 8 Вычислить ... (Математический анализ. Дифференциальное исчисление)

... точке Производной функции в точке M(x, y) в направлении вектора . называется Если функция дифференцируема , то производная в данном направлении вычисляется по. формуле , где α - угол между вектором s и осью OX Пользуясь определением ... ... , формуле для производной по направлению можно придать . вид : , где вектор so - орт вектора s, т е производная функции по данному направлению равна скалярному произведению градиента функции . на единичный вектор ... (Математический анализ. Дифференциальное исчисление)

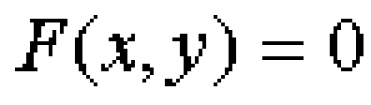... x называется функция , значения которой находятся . из уравнения , связывающего x, y и не разрешенного относительно y,.т е Производная неявной функции находится по следующей формуле :. Неявной функцией z аргументов x и y называется функция ... (Математический анализ. Дифференциальное исчисление)

... способы возникают в ходе развития новоевропейской механики и дифференциального . исчисления : скорость - это первая производная пути по времени (радиус-вектора ), ускорение -.производная скорости (вторая производная от радиус-вектора ); оба ... (Физические основы механики)

---

---