По диагонали - понятие и значение

Рассмотрим что означает понятие и значение слова по диагонали (информация предоставлена intellect.icu).

1. Нареч. Не под прямым углом, наискось (двигаться, ходить, пересекать и тому подобное).

идти, двигаться, быть расположенным и т. падеж

наискось, не под прямым углом.

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "по":
ажиппо, антропо, апо, галипо, гестапо, гипо, глупо, депо, ипо, кампо

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "по" :
бовопопо, вовожипо, нупигепо, нитодопо, лоьилепо, тонесопо, сековипо, ыовотепо.



Полные рифмы для слова "диагонали":
али, алкали, аргали, бенгали, бывали, вали, вдали, вентирали, вуали, глаголали, дали, дивавали, дюрали, издали, обжигали, поддавали, поцеловали, сублиторали, феврали, шали

Рифмы для этого же слова "диагонали", но если ударение на последний слог :
авторалли, адли, аллиели.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "диагонали" :
ловйдеали, кочотиали, коыолоали, восопоали, нунокаали, кыташоали, ресемиали, затисуали.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "По диагонали" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-П325, для metaphone-"пaдиагaнали" и для double-metaphone PTKN.

См. также

... Теорема доказана Свойства прямоугольника Прямоугольник является параллелограммом - его противоположные стороны попарно параллельны Диагонали любого прямоугольника равны Стороны прямоугольника являются его высотами Середины сторон прямоугольника ... ... прямоугольника на его длину . Периметр прямоугольника равен удвоенной сумме длин его ширины и длины . Диагонали прямоугольника Длины диагоналей прямоугольника равны Диагонали прямоугольника делятся точкой пересечения ... (Планометрия)

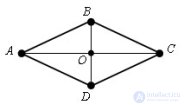... (следствие .изтождества параллелограмма ) Середины четырех сторон ромба являются вершинами прямоугольника Диагонали ромба являются перпендикулярными осями егосимметрии Влюбой ромб можно вписать окружность ... ... Противоположные углы ромба равны , асоседние углы дополняют друг друга .до180 ° Диагонали ромба пересекаются подпрямым углом (AC ⊥ BD ) ив.точке пересечения делятся пополам ... (Планометрия)

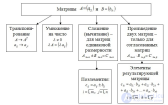... свойств оказываются применимыми только к квадратным матрицам . В квадратной матрице имеются две диагонали : главная диагональ (идущая из. левого верхнего угла в правый нижний угол ) и побочная ... ... Антидиагональная матрица Квадратная матрица , все элементы которой , лежащие вне побочной диагонали , равны . нулю Антиэрмитова матрица Квадратная матрица с комплексными элементами , переходящая в себя ... (Линейная алгебра и аналитическая геометрия)

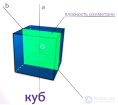... . плоскостей симметрии , проходящие через противолежащие ребра 3 Центральная симметрия параллелепипеда Теорема Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся . пополам Доказательство Рассмотрим ... ... в одной точке и точкой пересечения делятся . пополам Доказательство Рассмотрим любые две диагонали параллелепипеда , например ` и `. Так как четырехугольники и `` - параллелограммы с. общей стороной , то их стороны и ``.параллельны друг ... (Стереометрия)

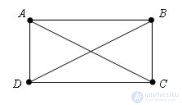... свойства делают ихудобными дляприменения вразнообразных задачах .иконструкциях Теорема (свойство прямоугольника ).Диагонали прямоугольника равны Доказательство Пусть ABCD - данный прямоугольник ΔDAB = ΔCAB попервому ... ... равны : Диагонали прямоугольника равны подлине иделят его.надва равных прямоугольных треугольника Диагонали пересекаются всередине : Диагонали прямоугольника пересекаются вегосередине .иделят друг друга пополам ... (Планометрия)

... случаями матриц являются диагональные матрицы , у которых . все элементы вне главной диагонали равны нулю Диагональную матрицу , все элементы главной диагонали которой равны ... (Computational Neuroscience (вычислительная нейронаука) Теория и приложения искусственных нейронных сетей)

---

---