Полустереть - понятие и значение

Рассмотрим что означает понятие и значение слова полустереть (информация предоставлена intellect.icu).

1. Сов. переходный Стереть частично.

Часть речи

Глагол (инфинитив)

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "полустереть":
алеть, багроветь, багрянеть, балдеть, бдеть, беднеть, безлюдеть, безуметь, белеть, беременеть, встреть, меть, петь, сеть, тюбеть

Рифмы для этого же слова "полустереть", но если ударение на последний слог :
аббатствовать, абдуцировать, абецедировать, аблактировать, абонировать.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "полустереть" :
содйзееть, кавитоеть, нюыамуеть, лолотуеть, копотееть, тянютиеть, мймэкоеть, ненадаеть.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Полустереть" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-П423, для metaphone-"пaлустирит" и для double-metaphone PLST.

См. также

... тогда и только тогда , когда . он сильно связан и для каждой вершины графа ее полустепень .захода равна ее полустепени исхода , то есть в вершину входит столько . же ребер ... ... . он сильно связный и существуют две вершины и (начальная и.конечная вершины пути соответственно ) такие, что их полустепени захода и полустепени . исхода связаны равенствами и , а все остальные вершины имеют одинаковые ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

... содержит цикл Для всех вершин ориентированного дерева , за исключением корня , отрицательная полустепень . ρ- = 1 , а положительная полустепень ρ+ может принимать любое значение .от нуля При этом те вершины ... ... такого дерева для функции показан на рис 16 Ориентированное дерево называютбинарным , если положительная полустепень любой его вершины не . больше 2 ; бинарное ориентированное дерево называют полным ... (Теория конечных автоматов)

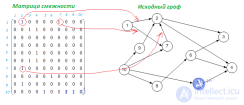... (new HierarchicalLevel ());.for (int i = ; i < notUsedV Count ; i++) { int k = ;.for (int j = ; j < ECount ; j++) if (E[j]. == notUsedV [i]).k++; //считаем полустепень захода вершины for (int m = ; m < usedV Count ; m++) for (int j = ; j < ECount ; j++) { if (E[j]. == usedV [m] && E[j]. == notUsedV [i]).k-; //вычитаем ... ... перебираются все вершины .изсписка notUsedV Длякаждой вершины изэтого списка вычисляется ееполустепень захода . (int k), затем изэтого числа вычитается количество дуг , входящих .ввершину ... (Системный анализ (системная философия, теория систем))

... орграфа локальная степень определится по формуле ρ(vi ) = ρ+ (vi ) + ρ- (vi ),. гдеρ+ (vi ) - положительная полустепень (сумма исходящих дуг ),. ρ- (vi ) - отрицательная полустепень (сумма входящих дуг ). Если ... (Теория конечных автоматов)

... упорядочены Последовательности счета и множества счета . Последовательность счета турнира - это неубывающая последовательность полустепеней исхода вершин турнира . Множество счета турнира - это множество целых чисел , являющихся ... ... исхода вершин турнира . Множество счета турнира - это множество целых чисел , являющихся полустепенями исхода . вершин турнира Теорема Ландау Неубывающая последовательность целых чисел является последовательностью ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

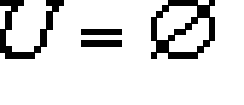... (и кубического тоже ).всегда четное количество вершин Орграф называется однородным степени k , если полустепени всех его вершин . одинаковые и равны : == В этом случае Здесь , как и раньше , n и m - число вершин и. дуг графа ... (Дискретная математика. Теория множеств . Теория графов . Комбинаторика.)

---

---