1. Сов. смотрите перебинтовываться

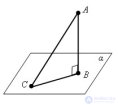 ... Перпендикуляром , опущенным из данной точки данную плоскость , называется отрезок , соединяющий . данную точку ... ... на прямой , перпендикулярной .плоскости Конец этого отрезка , лежащий в плоскости , называется основанием перпендикуляра Наклонной , проведенной из данной точки к данной плоскости , называется любой . отрезок , соединяющий ... (Стереометрия)
... Перпендикуляром , опущенным из данной точки данную плоскость , называется отрезок , соединяющий . данную точку ... ... на прямой , перпендикулярной .плоскости Конец этого отрезка , лежащий в плоскости , называется основанием перпендикуляра Наклонной , проведенной из данной точки к данной плоскости , называется любой . отрезок , соединяющий ... (Стереометрия)
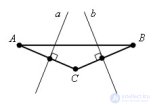 ... через середину отрезка перпендикулярно к нему , называют серединным . перпендикуляром или медиатрисой Теорема Серединные перпендикуляры к двум сторонам треугольника пересекаются Доказательство Пусть есть Δ ABC и прямые a, b - серединные перпендикуляры ... (Планометрия)
... через середину отрезка перпендикулярно к нему , называют серединным . перпендикуляром или медиатрисой Теорема Серединные перпендикуляры к двум сторонам треугольника пересекаются Доказательство Пусть есть Δ ABC и прямые a, b - серединные перпендикуляры ... (Планометрия)
 ... любой точки , не лежащей на данной прямой , можно опустить . на эту прямую перпендикуляр , и только один Доказательство Пусть a - данная прямая и не лежащая на этой прямой ... ... b проходила через точку A Тогда прямая b ⊥ a, так как b || с и с. ⊥ a Значит отрезок AB ⊥ a Теперь докажем единственность перпендикуляра AB Допустим , существует еще перпендикуляр , проходящий через точку A к прямой . a Тогда у треугольника ... (Планометрия)
... любой точки , не лежащей на данной прямой , можно опустить . на эту прямую перпендикуляр , и только один Доказательство Пусть a - данная прямая и не лежащая на этой прямой ... ... b проходила через точку A Тогда прямая b ⊥ a, так как b || с и с. ⊥ a Значит отрезок AB ⊥ a Теперь докажем единственность перпендикуляра AB Допустим , существует еще перпендикуляр , проходящий через точку A к прямой . a Тогда у треугольника ... (Планометрия)
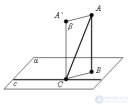 ... на плоскости перпендикулярна наклонной , то она перпендикулярна и. проекции наклонной Доказательство Аналогично теореме о трех перпендикулярах если прямая с перпендикулярна наклонной . CA , то она, будучи перпендикулярна и прямой CA `, перпендикулярна плоскости ... (Стереометрия)
... на плоскости перпендикулярна наклонной , то она перпендикулярна и. проекции наклонной Доказательство Аналогично теореме о трех перпендикулярах если прямая с перпендикулярна наклонной . CA , то она, будучи перпендикулярна и прямой CA `, перпендикулярна плоскости ... (Стереометрия)
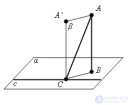 ... на плоскости через основание наклонной , перпендикулярна ее. проекции , то она перпендикулярна наклонной Доказательство Пусть AB – перпендикуляр к плоскости α, AC – наклонная и с. – прямая в плоскости α, проходящая через основание С наклонной Проведем прямую ... (Стереометрия)
... на плоскости через основание наклонной , перпендикулярна ее. проекции , то она перпендикулярна наклонной Доказательство Пусть AB – перпендикуляр к плоскости α, AC – наклонная и с. – прямая в плоскости α, проходящая через основание С наклонной Проведем прямую ... (Стереометрия)
 ... перпендикуляром двух скрещивающихся прямых называется отрезок с концами на. этих прямых , являющийся перпендикуляром к каждой из них Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра Оно равно ... (Стереометрия)
... перпендикуляром двух скрещивающихся прямых называется отрезок с концами на. этих прямых , являющийся перпендикуляром к каждой из них Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра Оно равно ... (Стереометрия)
Комментарии
Оставить комментарий