Параллелепипед - понятие и значение

Рассмотрим что означает понятие и значение слова параллелепипед (информация предоставлена intellect.icu).

1. Шестигранник, противоположные грани которого попарно параллельны.

В математике: призма, основанием к-рой служит параллелограмм.

1. Параллелепипеда, (от греческое parallelos - параллельный и epipedon - поверхность) ( математика ). Шестигранник, у к-рого противоположные грани равны и параллельны.

ПАРАЛЛЕЛЕПИПЕД

греческое , от parallelos., параллельный, и epidon, поверхность. Четырехсторонняя призма, у которой противоположные стороны параллельны между собой.

ПАРАЛЛЕЛЕПИПЕД

четырехгранная призма, у которой противоположные грани (прямоугольные четырехугольники или параллелограммы) равны и параллельны между собою.

-а, м. Мат.

Шестигранник, основаниями которого служат параллелограммы.

{Греч. παραλληλεπίπεδον}

Часть речи

Имя существительное

Словоформы

параллелепипеда, параллелепипеду, параллелепипедом, параллелепипеде, параллелепипеды, параллелепипедов, параллелепипедам, параллелепипедами, параллелепипедах

Синонимы

шестигранник, призма, ромбоэдр, многогранник

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "параллелепипед":
велосипед, логопед, мопед, мотовелосипед, мотопед, ортопед, параллелопипед, пед, торпед

Рифмы для этого же слова "параллелепипед", но если ударение на последний слог :
альфред, антиганимед, аред, балетовед.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "параллелепипед" :
тевитипед, луьусыпед, ретачыпед, гамюнопед, ридитапед, чэнарепед, ножахепед, репихыпед.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Параллелепипед" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-П644, для metaphone-"паралилипипит" и для double-metaphone PRLL.

См. также

... Построение тени параллелепипеда на эпюре ... (18 Тени и отражения)

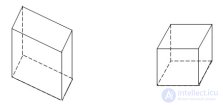... Прямоугольный параллелепипед , у которого основанием является прямоугольник , называется прямоугольным параллелепипедом . У прямоугольного параллелепипеда все грани - прямоугольники Прямоугольный параллелепипед , у которого все ребра равны , называется ... ... , у которого все ребра равны , называется кубом . Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами ... (Стереометрия)

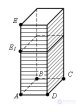... доказать Возьмем теперь куб , являющийся единицей измерения объема , и три прямоугольных . параллелепипеда с измерениями : a, 1 , 1 ; a, b, 1 ; a,.b, c Обозначим , их объемы , и V соответственно По доказанному Перемножая ... ... . ABCD и высотами AE и AE Будем считать для определенности ,.что < AE Пусть V и – объемы параллелепипедов Разобьем ребро AE параллелепипеда P на большое число n равных . частей Каждая из них равна ... (Стереометрия)

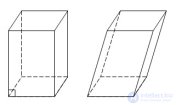... , в основании которой параллелограмм Параллелепипед называется прямым , если его боковые ребра перпендикулярны основаниям Параллелепипед называется наклонным , если его боковые ребра не перпендикулярны основаниям . Грани параллелепипеда , не ... (Стереометрия)

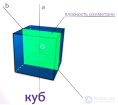... пересекаются в одной точке и делятся этой . точкой пополам Поэтому противоположные вершины параллелепипеда симметричны относительно этой точки Следовательно , каждый параллелепипед имеет центр симметрии - точку ... ... ребер и шесть . плоскостей симметрии , проходящие через противолежащие ребра 3 Центральная симметрия параллелепипеда Теорема Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся . пополам ... (Стереометрия)

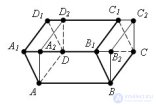... есть параллелепипед Проведем через ребро BC плоскость , перпендикулярную . основанию ABCD , и дополним наклонный параллелепипед треугольной призмой Отсечем .теперь от полученного тела треугольную призму плоскостью , проходящей ... ... плоскостью , проходящей через ребро AD . и перпендикулярной основанию ABCD Тогда получим снова параллелепипед Этот параллелепипед имеет объем , равный объему исходного параллелепипеда Достроенная призма и отсекаемая ... (Стереометрия)

---

---