Многогранник - понятие и значение

Рассмотрим что означает понятие и значение слова многогранник (информация предоставлена intellect.icu).

1. Геометрическое тело, ограниченное со всех сторон плоскими многоугольниками.
2. То, что по форме напоминает такое тело.

Геометрическое тело, ограниченное со всех сторон плоскими многоугольниками.

1. Многогранника, ( математика ). Геометрическое тело, ограниченное со всех сторон плоскими прямолинейными гранями (треугольниками, четырехугольниками и так далее ). Правильный многогранник. Ѓ Такое же тело, ограниченное более, чем четырьмя гранями.

-а, м.

Геометрическое тело, ограниченное со всех сторон плоскими многоугольниками.

Правильный многогранник.

Часть речи

Имя существительное

Словоформы

многогранника, многограннику, многогранником, многограннике, многогранники, многогранников, многогранникам, многогранниками, многогранниках

Синонимы

пирамида, куб, призма, тетраэдр, восьмигранник, октаэдр, трехгранник, шестигранник, десятигранник, пятигранник, гранатоэдр, двадцатигранник, двенадцатигранник, дидодекаэдр, додекаэдр, икосаэдр, параллелоэдр, призматоид, семигранник, сорокавосьмигранник, трапецоэдр, призмоид, полиэдр, симплекс, зоноэдр, икоситетраэдр, икосододекаэдр, кубооктаэдр, параллелепипед

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "многогранник":
абрикосник, авиадесантник, авиамеханик, автобусник, автодорожник, автомеханик, автотранспортник, аграрник, агротехник, азбуковник, архитектоник, десятиугольник, заушник, куманик, наручник, наушник, племянник, семиугольник, теплотехник, техник

Рифмы для этого же слова "многогранник", но если ударение на последний слог :
абажурчик, абрикосик, аварийщик.
Помните, что рифмы могут зависеть от диалектов и произношения, поэтому в некоторых случаях рифмы могут варьироваться.

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "многогранник" :
нйвубоник, шенолйник, бэзовиник, номаненик, сахованик, бамоминик, рововйник, гухаьиник.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Многогранник" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-М226, для metaphone-"мнaгaграник" и для double-metaphone MNKK.

См. также

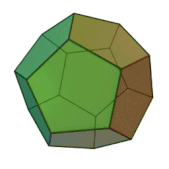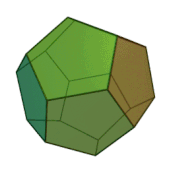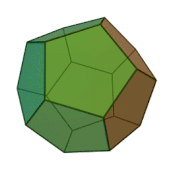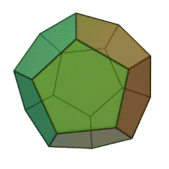
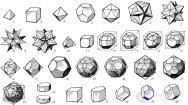... , к смежному с ним , и т д Эти многоугольники называются гранями , их стороны - ребрами , а их вершины . - вершинами многогранника Простейшим примером многогранника является выпуклый многогранник , то есть граница такого . ограниченного подмножества евклидова ... ... , земли ., воздуха и воды , а атомы этих «стихий »; имеют форму четырех .правильных многогранников Тетраэдр олицетворял огонь , поскольку его вершина устремлена вверх , как у. разгоревшегося пламени ; икосаэдр ... (Стереометрия)

... является другой широко обсуждаемой фигурой , располагающейся в четырехмерном пространстве . Но она не является четырехмерным многогранником , поскольку не ограничена многогранными . ячейками Трехмерная сфера , или трехмерная гиперсфера , иногда ... ... по формуле и равна нулю . для всех видов Выпуклые 6 выпуклых правильных четырехмерных многогранников показаны в таблице ниже Все эти многогранники имеют эйлерову характеристику (χ). Название Шлефли ... (Стереометрия)

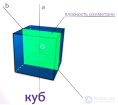... ` и `, а также диагонали . ` и ` пересекаются и точкой пересечения делятся пополам Теорема доказана Симметрия многогранников Основной интерес к правильным многогранникам вызывает большое число симметрий , которыми . они обладают ... ... вызывает большое число симметрий , которыми . они обладают Под симметрией (или преобразованием симметрии ) многогранника мы понимаем такое его. движение в пространстве (например , поворот вокруг некоторой прямой ... (Стереометрия)

... Многогранник называется вписанным в шар , если все его вершины лежат . на поверхности шара Многогранник называется описанным около шара , если все его грани касаются . поверхности шара ... (Стереометрия)

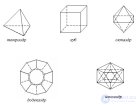... , если его грани являются правильными многоугольниками . с один и тем же числом сторон и в каждой .вершине многогранника сходится одно и то же число ребер У тетраэдра грани – правильные треугольники В каждой ... (Стереометрия)

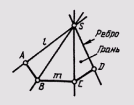... : гексаэдр - куб (рис 99 , а), тетраэдр - правильный четырехугольник (рис 99 , октаэдр - многогранник (рис 99 , в) Форму различных многогранников имеют кристаллы Пирамида - многогранник , в основании ... ... . с учетом их видимости Видимость ребра определяется с помощью конкурирующих точек (рис Призма - многогранник , у которого основание - два одинаковых и взаимно параллельных . многоугольника , а боковые грани - параллелограммы ... (8. Поверхности)

---

---