Вписанный - понятие и значение

Рассмотрим что означает понятие и значение слова вписанный (информация предоставлена intellect.icu).

1. прилагательное Ограниченный пределами какой -либо геометрической фигуры (в математике).

1. Вписанная, вписанное; вписан, вписана, вписано. 1. Прич. страдательное (причастие) прошедшее время время глагола от вписать. 2. только полная форма прилагательного формы. такой, вершины к-рого лежат на окружности (о многоугольниках), или такой,который является касательным к сторонам многоугольника (об окружности; средний род вписать в 3 значение ; математика ). Вписанный многоугольник. Вписанная окружность.

1.

Прич. страдательное (причастие) прошедшее время от вписать.

2.

в значение прилагательное Мат. Заключенный в пределы какой -либо геометрической фигуры с соблюдением определенных условий.

Вписанный треугольник.

Часть речи

Причастие (полное)

Словоформы

вписанного, вписанному, вписанным, вписанном, вписанная, вписанной, вписанную, вписанною, вписанное, вписанные, вписанных, вписанными

Синонимы

включенный, включивший, записавший, вставивший, внесший, занесший, поместивший, прописавший, поселивший, вовлекший, вовлеченный, вселивший, проставивший, доставленный, заметенный, засыпанный, внесенный, припорошенный, запорошенный, завеянный, заброшенный, закинутый, задутый, заснеженный, позанесенный, подброшенный, принесенный, привнесенный, внушенный

Рифмы

Данное слово имеет следующие слова-рифмы:

Полные рифмы для слова "вписанный":
абажурный, абактинальный, абдикационный, абдоминальный, аберрационный, абинный, абиогенный, абиссальный, абнормальный, абонементный, боскетный, голосемянный, званый, малосемейный, несравненный, полубольный, хлебный, чебуречный, швейный

Вымышленные слова-рифмы для этого же слова (с учетом частотности букв русского или английского языка) "вписанный" :
ненетоный, паповоный, веканыный, тыпазоный, вононаный, лосалуный, тямиданый, лорирюный.



Больше рифм

---

Цифровое произношение

Используя технологию и алгоритмы для преобразования "Вписанный" в числовой формат с целью облегчения их поиска, классификации или сопоставления для достижения цифрового произношения алгоритмами soundex-В250, для metaphone-"фписанaй" и для double-metaphone FPSN.

См. также

... Теорема Сторона a правильного связана с радиусом r вписанной окружности . формулой Доказательство Теорема доказана ... (Планометрия)

... Многогранник называется вписанным в шар , если все его вершины лежат . на поверхности шара Многогранник называется описанным около шара ... (Стереометрия)

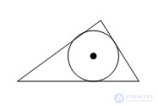... Окружность называется вписанной в треугольник , если она касается через все . его сторон Теорема Центр окружности , вписанной в треугольник , является точкой пересечения его биссектрис . Доказательство Пусть ABC данный , O – центр вписанной ... (Планометрия)

... , вписанный в окружность основания конуса , а вершиной является вершина .конуса Боковые ребра пирамиды , вписанной в конус , являются образующими конуса Касательной плоскостью к конусу называется плоскость , проходящая ... ... Плоскости боковых граней описанной пирамиды являются касательными плоскостями конуса Пирамидой , вписанной в конус , называется такая пирамида , основание которой есть. многоугольник , вписанный в окружность основания конуса ... (Стереометрия)

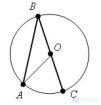... соответствующего центрального угла . Доказательство Пусть есть окружность с центром в точке O и угол . ABC , вписанный в эту окружность , так что одна из сторон .угла проходит через центр окружности Соединим точку ... (Планометрия)

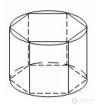... Призмой , вписанной в цилиндр , называется такая призма , у которой плоскостями . оснований являются плоскости оснований цилиндра ... (Стереометрия)

---

---